Радиус сходимости степенного ряда. Формула Коши-Адамара для радиуса сходимости степенного ряда.

1) Степенной ряд сходится абсолютно на некотором интервале 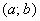. Иными словами, если мы выбираем любое значение «икс» из интервала 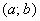и подставляем его в общий член степенного ряда, то у нас получается абсолютно сходящийся числовой ряд. Такой интервал 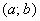и называется интервалом сходимости степенного ряда.

Радиус сходимости, если совсем просто, это половина длины интервала сходимости:

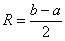
2) Степенной ряд сходится абсолютно при любом значении 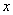. То есть, какое бы значение «икс» мы не подставили в общий член степенного ряда – в любом случае у нас получится абсолютно сходящийся числовой ряд. Интервал сходимости и область сходимости в данном случае совпадают: 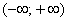. Радиус сходимости: 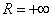. Рисунок приводить не буду, думаю, нет необходимости.

3) Степенной ряд сходится в единственной точке. Если ряд имеет вид 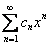, то он будет сходиться в единственной точке 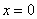. В этом случае интервал сходимости и область сходимости ряда тоже совпадают и равны единственному числу – нулю: 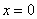. Если ряд имеет вид 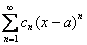, то он будет сходиться в единственной точке 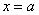, если ряд имеет вид 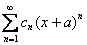, то, понятно, – в точке «минус а». Радиус сходимости ряда во всех случаях, естественно, нулевой: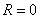

Радиус сходимости степенного ряда определяется по формуле Коши-Адамара

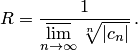
Здесь 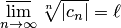— верхний предел последовательности 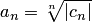. Он всегда существует (конечный или бесконечный), и притом единственный. В случае 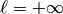полагают 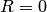, а в случае 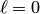полагают .

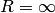20. Ряд Тейлора. Теорема Тейлора о разложимости функции в ряд Тейлора. Разложение основных элементарных функций в ряд Тейлора-Маклорена: e^x, sinx, cosx, (1+x)^a, ln(1+x).

Пусть функция 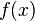бесконечно дифференцируема в некоторой окрестности точки 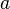. Формальный ряд

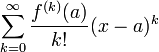
называется рядом Тейлора функции 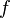в точке .

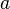В случае, если 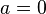, этот ряд также называется рядом Маклорена.

Пусть 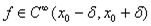. Тогда ряд 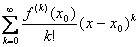называется рядом Тейлора функции 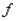в точке .

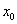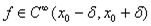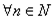Если , то по формуле Тейлора: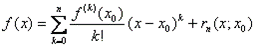

, где 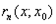- остаточный член формулы Тейлора, т.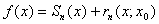е. , где 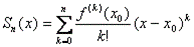- n-ая частичная сумма ряда Тейлора функции 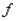в точке 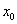. 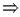ряд Тейлора сходится на 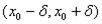тогда и только тогда, когда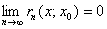

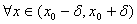
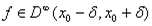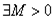
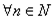
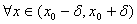
Пусть и 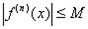, тогда на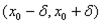

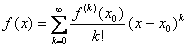
Доказательство:

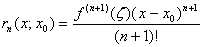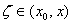, где - остаточный член формулы Тейлора в форме Лагранжа:

.

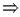
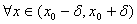
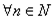
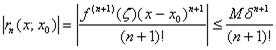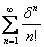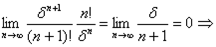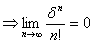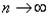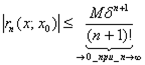
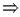
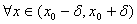
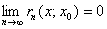
Рассмотрим ряд , по признаку Даламбера ряд сходится . Перейдем к пределу при в неравенстве 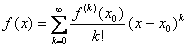на .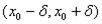

Теорема Тейлора

Пусть функция f(x) имеет в точке х = а и некоторой ее окрестности производные порядка до (n+1) включительно.{ Т.е. и все предыдущие до порядка n функции и их производные непрерывны и дифференцируемы в этой окрестности}.

2) Пусть х- любое значение из этой окрестности, но а ¹ х

Тогда между точками х и а найдется такая точка e, что справедлива формула:

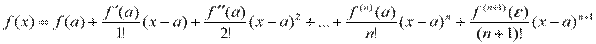
это выражение называется формулой Тейлора, а выражение:

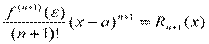
называется остаточным членом в форме Лагранжа.

Доказательство. Представим функцию f(x) в виде некоторого многочлена Pn(x), значение которого в точке х = а равно значению функции f(x), а значения его производных равно значениям соответствующих производных функции в точке х = а.

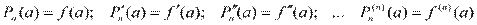(1)

Многочлен Pn(x) будет близок к функции f(x). Чем больше значение n, тем ближе значения многочлена к значениям функции, тем точнее он повторяет функцию.

Представим этот многочлен с неопределенными пока коэффициентами:
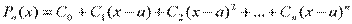(2)

Для нахождения неопределенных коэффициентов вычисляем производные многочлена в точке х = а и составляем систему уравнений:
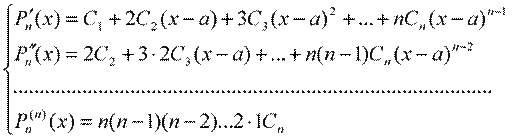(3)

Решение этой системы при х = а не вызывает затруднений, получаем:

…………………….

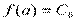
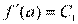
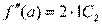
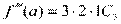
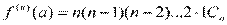
Подставляя полученные значения Ci в формулу (2), получаем:

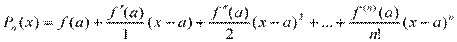
Как было замечено выше, многочлен не точно совпадает с функцией f(x), т.е. отличается от нее на некоторую величину. Обозначим эту величину Rn+1(x). Тогда:

f(x) = Pn(x) + Rn+1(x)

Теорема доказана.

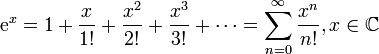
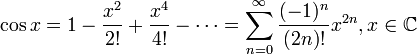
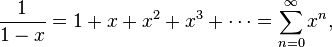для всех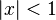

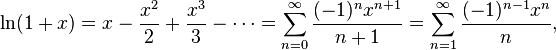для всех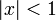

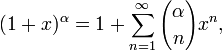для всех 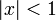и всех комплексных 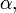где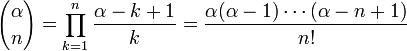

Функции многих переменных. Понятие n-мерного евклидового пространства. Множество точек евклидового пространства. Последовательность точек и ее предел. Определение функции нескольких переменных.

Выше мы говорили о функциях от одной переменной. Но можно говорить также о функциях двух, трех и вообще 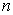переменных.

Функция от двух переменных определяется следующим образом. Рассматривается множество 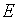пар чисел 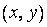. При этом имеются в виду упорядоченные пары. Это значит, что две пары 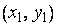и 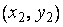считаются равными (совпадающими) тогда и только тогда, когда 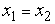и 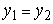. Если, в силу некоторого закона, каждой паре 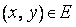приведено в соответствие число 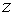, то говорят, что этим определена на множестве 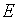функция 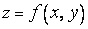от двух переменных 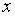и .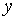

Так как каждой паре чисел 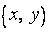соответствует на плоскости, где введена декартова система координат, точка с абсциссой 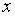и ординатой 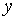, и, наоборот, каждой точке, таким образом, соответствует пара 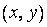, то можно говорить, что наша функция 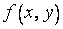задана на множестве 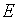точек плоскости.

Функцию 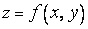от двух переменных изображают в трехмерном пространстве, где задана прямоугольная система координат 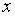, , 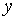, 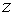в виде геометрического места точек 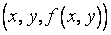, проекции которых 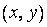принадлежат множеству 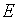определения .

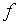Например, таким геометрическим местом для функции

,

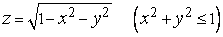является верхняя половина шаровой поверхности радиуса 1 с центром в нулевой точке.

В этом же духе можно определить функцию трех переменных. Областью ее определения может теперь служить некоторое множество упорядоченных троек чисел 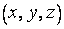или, что все равно, соответствующих им точек трехмерного пространства, где введена декартова система координат.

Если каждой тройке чисел (точке трехмерного пространства) 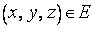, в силу некоторого закона, соответствует число 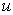, то говорят, что этим на 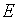определена функция .

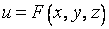Аналогично можно рассматривать множество 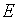упорядоченных систем 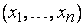из 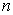чисел, где 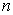- заданное натуральное число. Опять, если каждой такой системе, принадлежащей 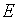, соответствует в силу некоторого закона число 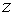, то говорят, что 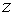есть функция от переменных 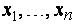, определенная на множестве 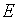, и записывается эта функция в виде .

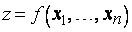В случае 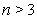в нашем распоряжении уже нет реального 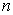- мерного пространства, чтобы использовать его для изображения систем 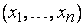в виде принадлежащих ему точек. Но математики выдумали 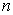-мерное пространство, и оно им благополучно служит, и притом не хуже, чем реальное трехмерное пространство. Именно, 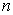-мерным пространством называется множество всевозможных систем 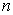чисел .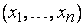

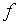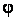Если две функции и от 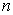переменных заданы на одном и том же множестве 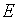систем 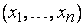- точек 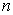-мерного пространства, - то можно определить сумму 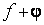, разность 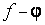, произведение 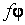и частное 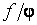, как функции, определенные на 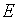при помощи равенств, аналогичных равенствам (2), где надо только числа 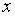заменить системами 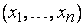. Естественным образом определяются также сложные функции, такие, как 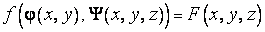, где 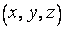- тройки чисел, принадлежащих некоторому множеству троек.

N-мерная евклидова геометрия — обобщение евклидовой геометрии на пространство большего числа измерений. Хотя физическое пространство является трёхмерным, и человеческие органы чувств рассчитаны на восприятие трёх измерений, N-мерная геометрия широко применяется в качестве математического инструмента при решении различного рода задач, связанных с манипулированием большим числом параметров (например, задачи оптимизации с большим числом переменных, задачи геометрической вероятности).

Система координат

Поскольку достаточно трудно работать с многомерными объектами, используя интуитивные представления трёхмерного мира, в N-мерной геометрии широко применяются аналитические методы. В качестве системы координат чаще всего используется прямоугольная декартова система с числом осей более трёх. Таким образом, некоторая точка А представляется в N-мерной геометрии как набор из N действительных чисел

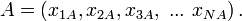
Несмотря на то, что интуитивно трудно представить себе четыре взаимно перпендикулярные оси, понятие перпендикулярности естественным образом обобщается из трёхмерного пространства на случай четырёх и более измерений. Так, скалярное произведение взаимно перпендикулярных векторов в случае N измерений также равно нулю.

Евклидово пространство однородно и изотропно, то есть его свойства, в том числе и формула для расстояния, не зависят ни от положения начала координат, ни от направления осей координат. Это даёт возможность свободно вращать и переносить объекты, не изменяя их геометрических свойств.

В N-мерном пространстве существуют подпространства всех размерностей 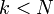, часто называемые гиперплоскостями или k-плоскостями, где k — размерность подпространства. Термин «гиперплоскость» используется также в узком смысле для обозначения подпространства размерности N–1 (коразмерности 1). Одномерное подпространство по аналогии с обычной геометрией называется прямой, двумерное подпространство — плоскостью. Никакого принципиального различия между k-плоскостью и k-пространством нет. Название «плоскость» подчёркивает тот факт, что объект находится внутри пространства большей размерности, то есть является подпространством. Например, в 4-пространстве обычное трёхмерное пространство является 3-плоскостью.

Можно показать, что в пространстве размерности N имеет место аналогичная ситуация — подпространство размерности k задаётся системой N–k линейных уравнений:

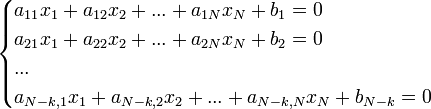
Если каждой упорядоченной паре чисел 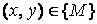по некоторому закону 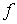поставлено в соответствие единственное действительное число 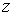, то говорят, что задана функция двух переменных 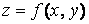или 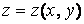. Числа 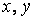называются при этом независимыми переменными или аргументами функции, а число 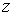– зависимой переменной.