R - радиус Земли.

Геометрическое место точек, имеющих одинаковую ординату У, представляет собой малый круг аАоО.1 (рисунок вверху), плоскость которого параллельна плоскости осевого меридиана. Радиус такого малого круга зависит от величины сферической ординаты Y и определяется по формуле r = R cos (Y/R). (114)
Сферический угол PNAoa = g при заданной точке Aо между ее меридианом и малым кругом, плоскость которого параллельна плоскости осевого меридиана, называется углом схождения или сближения меридианов. Величина его зависит от разности долгот между осевым меридианом и меридианом точки Аo и от широты этой точки. Определяется угол сближения меридианов по формуле g = (l - Lo)sin j. (115)
Знак угла сближения меридианов определяется расположением точек относительно осевого меридиана. Для точек, расположенных восточнее осевого меридиана, угол сближения меридианов будет иметь знак плюс; для точек, находящихся западнее осевого
На плоскости проекции сферические прямоугольные координаты X, Y изображаются в виде плоских прямоугольных координат х, у. При этом на проекции образуется сетка, составленная двумя семействами взаимно перпендикулярных параллельных прямых линий. Сферический угол схождения меридианов g в силу равноугольности проекции изображается на проекции плоским углом схождения меридианов g в виде угла между меридианами и линиями y = сonst.
§ 36. Применение карт в проекции Гаусса для навигационных целей
Для навигационных целей наиболее употребительны карты масштаба 1 : 100000 и крупнее. При таких масштабах ошибки графической прокладки определений места по сеткам изолиний будут незначительными и карты обеспечат точное вождение корабля по заданной линии пути с осуществлением коррекции курса на основе определений места.
Наиболее часто встречающимися навигационными задачами, решаемыми на карте в проекции Гаусса, являются:
— нанесение точки по заданным координатам или измерение (снятие) координат заданной точки;
— прокладка направлений (пеленгов);
— счисление пути корабля;
— прокладка определений места.
На проекции Гаусса, помимо координатных линий прямоугольной системы координат, прямыми изображаются линии дирекционных направлений, пересекающие километровые линии под постоянным углом a или Т.
Линия кратчайшего расстояния — ортодромия (для шара) — изображается на проекции Гаусса кривой, обращенной выпуклостью от осевого меридиана и составляющей со стягивающей ее хордой небольшой угол d''. Поправка d'' вследствие ее малой величины при решении навигационных задач не учитывается. Иными словами, при решении навигационных задач можно считать, что отрезки ортодромии на карте изображаются прямыми линиями.
Локсодромия на проекции Гаусса изображается кривой, обращенной выпуклостью от полюса. Стягивающая локсодромию хорда — прямая линия на карте — практически совпадает с изображением ортодромии вследствие малости угла d''. При сравнительно небольших плаваниях углы f1 и f2, которые локсодромия составляет со стягивающей ее хордой (рисунок), можно принять равными f1 = f2 = f, а локсодромию можно принять за дугу окружности.
Рисунок позволяет заключить:
Т = ИК - g1 - f и Т = ИК - g2 + f2;
- g1 - f = - g2 + f2,
Откуда
f = (g2 - g1) / 2. (130)
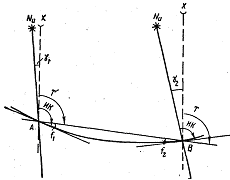
Следовательно, угол, который составляет локсодромия со стягивающей ее хордой, равен полуразности углов сближения меридианов в точках А и В, т. е. в начале и в конце локсодромии.
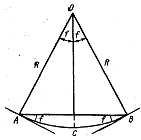
Принимая отрезок локсодромии AСВ за дугу окружности (рисунок), имеющую радиус, равный R, и центр в точке О, можно написать
ÈACB = Sлок = 2Rf;
AB = Sорт = 2Rsin f,
откуда
Sлок / Sорт = f / sin f.
Представив sin f в виде ряда и ограничиваясь по малости f двумя членами разложения, перепишем последнее выражение в виде
Sлок / Sорт = f / (f - f3 / 6) или Sлок / Sорт = 1 / (1 - f2 / 6),
Откуда
Sорт = Sлок - Sлок *(f2 / 6).
Обозначив Sлок - Sорт через Δs, получим Δs = Sлок (f2 / 6). (131)
Выражая f в минутах дуги, будем окончательно иметь
Δs = Sлок (f2 / 6) arc 1'. (132)
Расчеты по последней формуле показывают, что при Sлок =75 миль в j = 60° ошибка от замены локсодромии стягивающей ее хордой оказывается равной примерно 15 м. Если линию локсодромии длиной до 30 миль заменить отрезком хорды, то ошибка Δs не выйдет за пределы 10 м.
Учитывая сделанные выше выводы, можно следующим образом сформулировать рекомендации по решению отдельных навигационных задач на карте в проекции Гаусса.
1) Нанесение точки на карту по ее географическим координатам может быть сделано так же, как и на карте в проекции Меркатора, пользуясь делениями широты и долготы на ближайших рамках карты. Основанием для этого является то обстоятельство, что меридианы, являющиеся ортодромиями, изображаются на проекции Гаусса практически прямыми линиями; параллели, являющиеся частным случаем локсодромии, в пределах 15—20 см также могут быть приняты за прямые. Кроме того, и меридианы и параллели длиной 15—20 см можно принимать за параллельные между собой прямые.
2) Пеленги на карте прокладываются прямыми линиями. Прокладка пеленга на карте должна производиться относительно меридиана, ближайшего к начальной точке пеленга.
3) При ведении счисления путь корабля прокладывается на карте в виде прямой линии под углом относительно ближайшего к начальной точке пути меридиана, равным ИК ± f. Знак поправки за кривизну локсодромии f на карте в проекции Гаусса находится с помощью чертежа с учетом, что локсодромия на карте обращена выпуклостью от ближайшего полюса. При f £ 0,5° можно на карте прокладывать ИК без исправления поправкой.
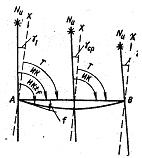
Другой прием прокладки линии пути (курса) состоит в том, что заданное направление движения корабля между двумя точками (ИК) прокладывается относительно меридиана, расположенного примерно посредине между точками A и B без всяких поправок. Линию пути (курса) можно откладывать и относительно вертикальных километровых линий (линии у = const). При этом угол между линией пути (курса) и линией х — дирекционный курс Т — равен
T = ИК - gср,
Где
gср = (g1 + g2) / 2, g1 и g2— углы сближения меридианов в точках А и В.
4) Пройденное по заданному курсу (пути) расстояние откладывается по прямой без учета поправок за кривизну кратчайших линий и поправки Δs, которые при графической прокладке практически ничтожны.
5) Прокладка определений места на проекции Гаусса ничем практически не отличается от прокладки на карте в проекции Меркатора, если опорные пункты располагаются в пределах рамки карты.
§ 37. Топографические карты, их номенклатура и использование в кораблевождении
Карты, изображающие отдельные участки суши, принято называть топографическими. В отличие от топографических карты, охватывающие целые материки или очень большие участки земной поверхности, называются географическими.
Советские топографические карты масштаба 1 : 500000 и крупнее составляются в проекции Гаусса; карта масштаба 1 : 1 000 000 составляется как в проекции Гаусса, так и в проекции международной карты мира. Географические карты могут составляться в различных проекциях. Математическая основа топографических карт строится по размерам эллипсоида Красовского в единой системе геодезических координат в шестиградусных зонах. Советские топографические карты составляются по обобщенным инструкциям и наставлениям и могут использоваться всеми ведомствами и учреждениями СССР. Иными словами, топографические карты являются многоцелевыми картами. Рамки топографических карт в виде трапеций образуются линиями картографической сетки меридианов и параллелей. Таким образом, любая топографическая карта представляет собой изображение участка земной поверхности, напоминающего по форме сфероидическую трапецию, ограниченную двумя меридианами и двумя параллелями. Вследствие того что топографические карты строятся, как правило, для шестиградусных зон, масштаб в пределах листа карты сохраняется практически постоянным и равен масштабу, указанному в заголовке карты.
На топографических картах показываются следующие элементы: сооружения на местности, населенные пункты, дорожная сеть, рельеф местности, водные объекты суши, в том числе береговая черта, почвенно-растительный покров, ориентиры, объекты связи.
Для покрытия земной поверхности топографическими картами различных масштабов существует определенная система нарезки (разграфка) карт. В Советском Союзе для всех топографических карт масштаба 1 : 1 00000,0 и крупнее до масштаба 1 : 10000 включительно принята нарезка карт по меридианам и параллелям.
Размеры сфероидической трапеции, изображаемой на топографических картах различных масштабов
| Интервал | 1:1 000 000 | 1:500 000 | 1:200 000 | 1:100 000 | 1:50 000 | 1:25 000 | 1:10 000 |
| Δφ | 4° | 2° | 40' | 20' | 10' | 5' | 2,5' |
| Δλ | 6° | 3° | 1° | 30' | 15' | 7,5' | 3.75' |
Каждый лист карты в зависимости от масштаба имеет свое обозначение. Система условных обозначений буквами и цифрами отдельных листов топографических карт различных масштабов называется номенклатурой карт.
В основу нарезки и номенклатуры топографических карт положен лист карты масштаба 1 : 1 000000, охватывающий участок земной поверхности размерами 4° по широте и 6° по долготе. Таким образом, вся земная поверхность делится на колонны — между меридианами и ряды — между параллелями. Каждый ряд сфероидических трапеций имеет разность широт 4°, и каждая колонна имеет разность долгот 6°. Счет рядов ведется от экватора до полюсов, и ряды в северном полушарии обозначаются латинскими буквами А, В, С, D, Е, F и т. д. (рисунок). Территория СССР располагается в пределах рядов I, J, К, L, М, N, О, Р, Q, R, S, Т. Колонны обозначаются арабскими цифрами от 1 до 60; счет их ведется от меридиана 180° к востоку.
Обозначение каждой из карт в масштабе 1 : 1000000 слагается из обозначения ряда и колонны. Так, например, миллионная карта, на которой помещен Тбилиси, имеет обозначение К—38.
Нарезка и номенклатура карт масштабов крупнее миллионной осуществляются путем соответствующего деления миллионной карты на более мелкие участки. Так, каждый лист карты масштаба 1 :500 000 составляет четверть листа миллионной карты. Для составления карт в масштабе 1:200000 миллионная карта делится на 36 частей, обозначаемых римскими цифрами от I до XXXVI.

Номенклатура карт в масштабе 1 :500 000 слагается из обозначения карты масштаба 1 : 1 000 000 и соответствующей ей четверти, обозначаемой буквами русского алфавита А, Б, В, Г (например, N—35— Г).
Карты в масштабе 1:200000 обозначаются номером карты масштаба 1 : 1 000 000 с добавлением номера соответствующей ее части (например, N—35—XII).
Карты масштаба 1 : 100000 получаются делением листа миллионной карты на 144 части, каждая из которых охватывает/ район, ограниченный разностью параллелей Δφ = 20' и по долготе Δλ = 30'. Номенклатура стотысячной карты составляется из обозначения карты масштаба 1:1000000 и номера соответствующей трапеции (например, N—35—24).

При составлении карт в масштабе 1:50000 лист карты в масштабе 1 : 100 000 разбивается на четыре части, каждая из которых обозначается буквами русского алфавита А, Б, В, Г. Обозначаются карты масштаба 1 : 50 000 номенклатурой карты масштаба 1 : 100 000 с добавлением одной из указанных букв (например,
N - 35 — 12 — Б).
Схема расположения листов карт масштабов 1 :500 000, 1 :200 000, 1 : 100000, 1 : 50000 на листе карты масштаба 1:1 000 000 показана на рисунке.
В дальнейшем нарезка карт масштабов 1 :25 000 и 1 : 10000 производится, как показано на рисунке. (Кстати, обозначения на этом рисунке следующие:
- жирная сплошная линия - нарезка листов карты М 1:500 000;
- тонкая сплошная линия - нарезка одинарных листов М 1:200 000;
- пунктирная линия - нарезка счетверенных листов М 1:200 000).
Например, карта в масштабе 1:25000 имеет номенклатуру N—35—12—Б—б, а карта масштаба 1 : 10000 обозначается N—35—12—Г—б—4.

Номенклатура карты, т. е. ее обозначение, надписывается над ее верхней рамкой, номенклатура соседних листов показывается мелким шрифтом в средней части рамок. В нижней части листа карты под рамкой показывается схема расположения прилегающих к данной карте листов других карт.
Для удобства и быстроты определения, номенклатуры того или иного листа топографической карты составляются и издаются так называемые сборные таблицы, представляющие собой одноцветные карты мелкого масштаба, на которых в виде прямоугольников или трапеций изображены листы карты соответствующих масштабов. Пользование такими сборными таблицами обычно затруднений не вызывает.
Методика решения навигационных задач на топографических картах определяется картографической проекцией, положенной в основу их построения, и условными обозначениями, принятыми для изображения нагрузки.
СЧИСЛЕНИЕ ПУТИ КОРАБЛЯ
§ 46. Основные понятия и определения
Корабль в плавании непрерывно меняет свое место относительно окружающей обстановки: берегов, островов, дна и т. д. Для осуществления кораблевождения по избранному безопасному пути штурман располагает способом, позволяющим ему непрерывно следить за местом корабля и путем, по которому он перемещается. Этот способ называется счислением пути корабля или сокращенно счислением.
Сущность счисления состоит в том, что по известным исходному месту, направлению, скорости и времени перемещения корабля рассчитывают его место и путь на любой момент времени. Таким образом, счислением пути корабля называется совокупность действий, имеющих целью получить на любой момент времени место и путь корабля на основе знания исходного места, направления, скорости и времени его перемещения. Место, полученное способом счисления по показаниям корабельных приборов (компаса, лага, часов), называется счислимым местом. Оно может быть получено графическим способом на морской карте или с помощью аналитического способа счисления по формулам и таблицам. Аналитическое и графическое счисление может выполняться штурманом вручную или с помощью автоматических счислителей и прокладчиков.
В настоящей главе рассматривается графический способ счисления пути корабля, выполняемый штурманом вручную. Корабль под влиянием работы движителей (гребных винтов) перемещается относительно вод ной среды в направлении своей диаметральной плоскости. Направление этого перемещения указывается компасами; скорость перемещения и проходимое кораблем расстояние измеряются лагами или вычисляются по времени и числу оборотов гребных винтов, показываемому тахометрами.
Помимо движителей, на корабль обычно действуют такие гидрометеорологические факторы, как течение, ветер и вызываемое им волнение. Явление перемещения корабля под воздействием течения носит название снос корабля течением. Явление перемещения корабля под влиянием ветра называется дрейфом.
Для ведения счисления пути корабля необходимо знать и учитывать:
— исходное место корабля φ, λ ;
— его истинный курс и скорость ИК, V ;
— время движения корабля данным курсом t.
При наличии в районе плавания течения, ветра и волны необходимо, кроме того, учитывать:
— снос корабля течением, т. е. знать и учитывать элементы течения — его направление и скорость;
— дрейф a ;
— время t' действия на корабль течения, ветра и других гидрометеорологических факторов.
Все эти величины называются элементами счисления.
К счислению пути корабля предъявляются следующие требования:
— счисление должно вестись непрерывно, чтобы в любой момент времени можно было видеть положение и путь корабля относительно окружающей обстановки;
— счисление должно быть точным, чтобы обеспечить навигационную безопасность плавания и решение задач, поставленных кораблю;
— счисление должно быть достаточно простым и наглядным.
Графический способ счисления часто называют навигационной прокладкой. Однако следует иметь в виду, что навигационная прокладка — понятие более широкое: оно, помимо счисления, включает в себя нанесение на карту обсервованных мест корабля, получаемых на основе измерения различных навигационных параметров.
§ 47. Элементарные задачи навигационной прокладки, решаемые на карте в проекции Меркатора
Как графическое счисление, так и навигационная прокладка в целом в значительной своей части состоят из решения на карте ряда элементарных задач.
К этим задачам относятся:
— нанесение точки на карту по заданным координатам;
— снятие (измерение) координат заданной точки;
— измерение расстояний между заданными точками;
— прокладка от заданной точки заданных направлений;
— измерение направлений между заданными точками;
— перенос заданной точки с одной карты на другую.
Перечисленные задачи решаются на карте в проекции Меркатора с помощью прокладочного инструмента, в комплект которого входят циркуль-измеритель, штурманский транспортир и параллельная линейка. Вместо транспортира и линейки могут использоваться два прямоугольных треугольника, сделанные из прозрачного материала, на одном из которых нанесены градусные деления; может использоваться также и специальная механическая прокладочная линейка, входящая в комплект автопрокладчика.
Рассмотрим, как с помощью прокладочного инструмента решаются простейшие задачи навигационной прокладки.
Задача 1. По заданным широте и долготе нанести точку на карту.
Задача решается с помощью параллельной линейки и циркуля.
На боковой рамке карты отмечают деление, соответствующее заданной широте; приложив параллельную линейку к параллели, ближайшей к этому делению, перемещают линейку так, чтобы ее срез пришелся на отмеченное деление. Затем, не сдвигая линейки, отмечают на нижней или на верхней рамке карты деление, соответствующее заданной долготе, и, сняв циркулем отрезок от этого деления до ближайшего меридиана, откладывают его вдоль среза линейки от того же меридиана.
Циркулем делается слабый укол, который и обозначит точку с заданными координатами.
Задача 2. Снять с карты широту и долготу данной точки.
Задача решается с помощью циркуля. Поставив одну ножку циркуля в данную точку, раздвигают его так, чтобы вторая ножка пришлась на ближайшую параллель. Проведя циркулем часть окружности, убеждаются, что ножка его касается этой параллели. Затем, не изменяя раствора циркуля, прикладывают одну его ножку к той же параллели на боковой рамке карты, а другую вдоль рамки к северу или к югу от данной параллели соответственно тому, севернее или южнее этой параллели находится -заданная точка. Слабый укол второй ножки циркуля отметит искомую широту данной точки. Для снятия долготы снова ставят одну ножку циркуля в данную точку и, раздвинув его до ближайшего меридиана, описывают второй ножкой дугу окружности, касательную меридиану. Не изменяя раствора циркуля, прикладывают одну ножку его к тому же меридиану на верхней или нижней рамке карты, а другую вдоль рамки к Ost или W от этого меридиана соответственно тому, с какой стороны от него находится данная точка. Слабый укол циркуля отметит искомую долготу данной точки.
Задача 3. Измерение расстояния между двумя точками.
Задача решается с помощью циркуля. Устанавливают одну ножку циркуля в первую точку, а другую— во вторую и, не изменяя раствора циркуля, переносят его на боковую рамку карты в широте, соответствующей измеряемому расстоянию, где и подсчитывается число миль, оказавшееся в растворе циркуля. Если расстояние между точками большое и не может быть снято одним раствором циркуля (угол между ножками циркуля не должен быть более 90°), то его измеряют по частям, беря каждую часть в соответствующей широте.
Задача 4. От данной точки на карте проложить заданное направление.
Задача решается с помощью линейки и транспортира. Транспортир кладут на карту вблизи данной точки так, чтобы нижний срез его линейки составил с меридианом приблизительно заданное направление, а цен тральный штрих совпал с ближайшим меридианом. Затем, не смещая центрального штриха от меридиана, поворачивают транспортир вправо или влево до тех пор, пока деление транспортира, соответствующее заданному направлению, не совпадет точно с меридианом. Добившись совпадения, проверяют, не сместился ли центральный штрих транспортира с линии меридиана, затем к буртику транспортира плотно прикладывают параллельную линейку. После этого убирают транспортир и, сохраняя заданное направление, подводят срез линейки к данной точке, от которой и проводят тонко очиненным карандашом линию. Это и будет линия заданного направления. Для проверки правильности положения линейки рекомендуется, не меняя ее направления, еще раз приложить транспортир к срезу линейки у ближайшего меридиана. Если заданное направление близко к 0 или 180°, то транспортир следует прикладывать к параллели и устанавливать его на отсчет, отличающийся от заданного направления на 90°.
Задача 5. Определить направление проложенной на карте линии.
Задача решается с помощью транспортира и линейки. Точно совместив параллельную линейку с проложенной на карте линией курса или пеленга, прикладывают к ее срезу транспортир таким образом, чтобы его центральный штрих совпал с одним из меридианов. Отсчет на транспортире покажет величину (в градусах и долях градуса) определяемого направления (курса или пеленга).
Задача 6. Перенести точку с одной карты на другую.
Задача решается с помощью линейки, транспортира и циркуля и может быть выполнена или по пеленгу и расстоянию от ориентира, или по географическим координатам точки.
По пеленгу и расстоянию. На первой карте измеряют истинный пеленг и расстояние от какого-либо приметного точечного ориентира (маяк, тригонометрический знак), нанесенного на обеих картах, до заданной точки и записывают их. Затем прокладывают от того же ориентира на второй карте по этому истинному пеленгу то же расстояние в масштабе второй карты. Для контроля те же действия повторяют еще раз, но теперь следует измерять на первой карте и прокладывать на второй карте пеленг и расстояние от другого ориентира.
По географическим координатам. На первой карте измеряют широту и долготу заданной точки и записывают их. По снятым координатам точка наносится на второй карте. Для контроля измеряются широта и долгота нанесенной точки на второй карте и сравниваются с координатами заданной точки на первой карте.
§ 48. Графический способ счисления по показаниям компаса, лага и часов
При отсутствии ветра корабль под влиянием работы движителей (гребных винтов) перемещается относительно воды в направлении своей диаметральной плоскости. Если при этом отсутствует и течение, то это направление можно считать совпадающим с направлением перемещения корабля относительно грунта (дна моря).
 Проложив на карте (рисунок) от исходной точки А прямую, составляющую с меридианом карты угол, равный истинному курсу корабля, получим линию курса, по которой перемещается корабль.
Проложив на карте (рисунок) от исходной точки А прямую, составляющую с меридианом карты угол, равный истинному курсу корабля, получим линию курса, по которой перемещается корабль.
Расстояние, проходимое кораблем, может быть рассчитано по показаниям лага или по скорости хода корабля и времени. Для этого в тот момент, когда корабль находился в исходной точке счисления A, замечаются время по часам Т1 и отсчет лага ол1. В заданный момент, т. е. по истечении некоторого промежутка времени, эти действия повторяются: вновь замечаются время по часам T2 и отсчет лага ол2.
Расстояние, пройденное кораблем за время t = T2 - T1, может быть рассчитано по лагу Sл = кл (ол2—ол1) или по скорости хода корабля и времени Sоб = Vоб * t .
Проложив это расстояние от исходной точки А по линии курса, получим точку В, соответствующую месту корабля в момент T2 при отсчете лага ол2. Полученная таким путем точка В называется счислимым местом корабля и обозначается небольшой черточкой, перпендикулярной линии курса. Аналогичными действиями можно найти место корабля на следующий момент времени Тз при отсчете лага олз и т. д.
Вдоль линии курса надписывается компасный курс корабля и затем в скобках—поправка компаса с ее знаком. Около каждой счислимой точки делается надпись дробью: в числителе—часы и минуты, в знаменателе — отсчет лага. Дробная черта всегда проводится параллельно параллели с помощью линейки, концы линии не должны выступать за стороны воображаемого прямоугольника, окаймляющего цифры дроби. Высота каждой цифры должна быть равна примерно 4 мм.
Необходимым условием точности счисления является постоянный контроль всех измерений и расчетов. Нужно твердо помнить, что на карте прокладываются только истинные курсы и истинные пеленги, а пройденное кораблем расстояние снимается циркулем с боковой рамки карты в той широте, в которой лежит измеряемое расстояние.
Графическое счисление следует вести аккуратно и чисто, без помарок, тонко очиненным карандашом; линии курсов проводить тонкие, но ясные. Слишком твердый карандаш царапает карту, слишком мягкий — размазывается на ней. Резинка должна быть мягкой, карандашной. Лучше всего для работы на карте иметь отдельные средней твердости (ТМ, Т, М) карандаши, а записи наблюдений в записной книжке штурмана (ЗКШ) и навигационном журнале производить более мягкими карандашами.
§ 49. Циркуляция корабля. Способы учета циркуляции в прокладке
Способность корабля изменять направление своего движения и двигаться по криволинейной траектории под действием руля, выведенного из диаметральной плоскости, или под действием машин, или того и другого вместе называется поворотливостью. Криволинейная траектория, которую описывает центр тяжести корабля, движущегося при выведенном из диаметральной плоскости руле, называется циркуляцией. Рассмотрим характер циркуляции корабля, а затем приемы учета циркуляции при прокладке.
Предположим, на корабле, следовавшем прямолинейным курсом, когда он находился в точке Н (рисунок), была подана команда о перекладке руля. На передачу, репетование рулевым и исполнение команды потребуется некоторое время, в течение которого корабль
 продолжает следовать прежним курсом. Как только руль будет переложен, на корабль начнут действовать гидродинамические силы, отклоняющие корму в сторону, противоположную стороне перекладки руля; в ту же сторону смещается первоначально и центр тяжести корабля (участок АВ). Курс корабля начинает изменяться в ту сторону, куда положен руль; корабль начинает поворачивать (катиться) в нужную сторону. При этом возникают гидродинамические силы, действующие на корпус корабля и вызывающие изменение направления движения. Центр тяжести корабля описывает кривую ВСД, носящую название кривой циркуляции или просто циркуляции.
продолжает следовать прежним курсом. Как только руль будет переложен, на корабль начнут действовать гидродинамические силы, отклоняющие корму в сторону, противоположную стороне перекладки руля; в ту же сторону смещается первоначально и центр тяжести корабля (участок АВ). Курс корабля начинает изменяться в ту сторону, куда положен руль; корабль начинает поворачивать (катиться) в нужную сторону. При этом возникают гидродинамические силы, действующие на корпус корабля и вызывающие изменение направления движения. Центр тяжести корабля описывает кривую ВСД, носящую название кривой циркуляции или просто циркуляции.
Промежуток времени от момента подачи команды на руль до момента, когда курс корабля начинает изменяться, называется мертвым промежутком или предварительным периодом циркуляции. Расстояние ВВ', на которое центр тяжести корабля смещается в сторону, противоположную стороне поворота, называется обратным смещением корабля на циркуляции. Обычно оно не превышает половины ширины корабля и при прокладке им пренебрегают.
Продолжительность мертвого промежутка у разных кораблей неодинакова и зависит от времени, необходимого на перекладку руля, инерции корабля, влияния ветра и волнения и при неблагоприятных условиях может достигать одной минуты.
Продолжительность мертвого промежутка циркуляции штурман должен хорошо знать и всегда учитывать, с тем чтобы начало фактического поворота корабля возможно точнее совпало с рассчитанной и нанесенной на карту точкой начала поворота.
В начальный период циркуляция несколько отличается от окружности (дуга AВС) и не имеет постоянного радиуса, но после поворота на 90—120° радиус ее становится постоянным, и установившаяся циркуляция СДЕ практически представляет собой дугу окружности. Во время циркуляции диаметральная плоскость корабля не совпадает с касательной к траектории центра тяжести корабля, а составляет с ней некоторый угол Qц, называемый углом дрейфа на циркуляции; при этом нос корабля направлен внутрь циркуляции.
Расстояние В'Д между линией первоначального курса корабля и точкой Д циркуляции, где находится центр тяжести корабля после поворота на первые 180°, называется тактическим диаметром циркуляции (Дц). Расстояние ДЕ между точками циркуляции, соответствующими повороту на последующие 180°, носит название диаметра Ду установившейся циркуляции. Время, в течение которого корабль совершает поворот на первые 180°, носит название полупериода циркуляции и обозначается t180°.
Во время циркуляции сопротивление воды движению корабля увеличивается и фактическая скорость корабля становится меньшей, чем при том же числе оборотов гребных винтов на прямолинейном курсе. Это явление носит название потери скорости на циркуляции. Она может достигать 50—60%.
Из элементов циркуляции наибольшее значение для счисления имеют тактический диаметр и полупериод циркуляции. Тактический диаметр циркуляции обычно выражается в кабельтовых или в метрах. Он зависит от ряда факторов, к которым относятся, в частности, конструктивные особенности корабля (его длина, ширина, водоизмещение, площадь пера руля и т. д.). Для данного корабля эти факторы можно считать постоянными, а тактический диаметр—зависящим главным образом от угла перекладки руля. Чем больше угол перекладки руля, тем меньше диаметр циркуляции. На величину тактического диаметра циркуляции влияют также волнение моря и ветер; кроме того, в незначительной степени оказывают влияние также скорость хода корабля, его дифферент и осадка.
Полупериод циркуляции зависит главным образом от скорости хода корабля и угла перекладки руля. С увеличением скорости, хода и угла перекладки руля он уменьшается. При графическом счислении циркуляция учитывается, если прокладка ведется на картах масштаба I : 500 000 и крупнее. Циркуляция может учитываться графическими способами или, если их точность недостаточна, с помощью специальных таблиц.
Графический учет циркуляции основан на приближенном представлении циркуляции корабля как дуги окружности с диаметром, равным тактическому диаметру циркуляции. Величина тактического диаметра циркуляции при разных углах перекладки руля определяется на основе наблюдений, выполняемых при определении маневренных элементов корабля, и заносится в справочные таблицы штурмана. При учете циркуляции могут встречаться две частные задачи.
Задача 1.
Заданы курс и линия первоначального курса; курс, на который нужно повернуть; момент времени и отсчет лага начала поворота (они замечаются в тот момент, когда корабль начал катиться).
Найти точку конца поворота, через которую должна быть проложена линия нового курса.
Эта задача решается следующим образом (рисунок внизу слева).
 На линии первоначального курса приемами, разобранными в предыдущем параграфе, наносится точка начала поворота В. Из нее в сторону поворота корабля перпендикулярно первоначальному курсу проводится прямая линия, по которой откладывается отрезок ВО, равный в масштабе карты радиусу циркуляции корабля Rц.
На линии первоначального курса приемами, разобранными в предыдущем параграфе, наносится точка начала поворота В. Из нее в сторону поворота корабля перпендикулярно первоначальному курсу проводится прямая линия, по которой откладывается отрезок ВО, равный в масштабе карты радиусу циркуляции корабля Rц.
Из полученной таким образом точки О—центра циркуляции—раствором циркуля, равным (в масштабе карты) радиусу циркуляции, проводится дуга окружности. Затем параллельная линейка с помощью транспортира устанавливается в направлении нового истинного курса корабля и подводится так, чтобы срез линейки касался проведенной ранее окружности. Из точки касания С проводится прямая, представляющая собой линию нового курса корабля. В точке С заканчивается циркуляция, начинается новый курс. Чтобы найти точку конца поворота С более точно, из центра циркуляции опускается перпендикуляр на линию нового курса — его основание и явится точкой конца поворота.
Задача 2.
3аданы линия первоначального курса корабля и линия нового курса.
Найти точку, в которой корабль должен начать поворот, чтобы после циркуляции оказаться на заданной линии курса, и точку конца поворота.
Эту задачу приходится решать при повороте на линию створа, на ось фарватера при плавании в узкостях и т. д. Она решается следующим образом (рисунок слева внизу).
 Параллельно линии первоначального курса в расстоянии от нее, равном радиусу циркуляции Rц, проводится вспомогательная прямая ЕF. На этой линии подбирается такая точка О, чтобы окружность, проведенная из нее как из центра радиусом, равным радиусу цирууляции (в масштабе карты), касалась как линии первоначального, так и линии заданного курса. Первая из найденных таким образом точек касания А есть искомая точка начала поворота; вторая В — конца поворота. Чтобы нанести эти точки более точно, из центра циркуляции О надо опустить перпендикуляры на линию первоначального курса и на линию заданного курса. Команду на руль следует подавать, не доходя до точки А на расстояние, проходимое кораблем за мертвый промежуток времени.
Параллельно линии первоначального курса в расстоянии от нее, равном радиусу циркуляции Rц, проводится вспомогательная прямая ЕF. На этой линии подбирается такая точка О, чтобы окружность, проведенная из нее как из центра радиусом, равным радиусу цирууляции (в масштабе карты), касалась как линии первоначального, так и линии заданного курса. Первая из найденных таким образом точек касания А есть искомая точка начала поворота; вторая В — конца поворота. Чтобы нанести эти точки более точно, из центра циркуляции О надо опустить перпендикуляры на линию первоначального курса и на линию заданного курса. Команду на руль следует подавать, не доходя до точки А на расстояние, проходимое кораблем за мертвый промежуток времени.
Табличные способы учета циркуляции.
При всей простоте и наглядности графического учета циркуляции он обладает существенным недостатком — низкой точностью. Поэтому в случаях, когда необходим более точный учет циркуляции, прибегают к табличным способам. Основные зависимости, лежащие в основе табличных способов учета циркуляции, также базируются на представлении циркуляции как дуги окружности, радиус которой равен половине тактического диаметра циркуляции. Для учета циркуляции этим способом, кроме радиуса, необходимо знать следующие элементы циркуляции:
a — угол поворота корабля (угол между линиями старого и нового курсов);
Кср — промежуточный курс;
Sa — длина пути поворота на угол a (плавание на циркуляции);
ta — время поворота на угол a;
q — курсовой угол промежуточного курса;
а — промежуточное плавание (длина линии промежуточного курса);
d1 — расстояние до линии нового курса по линии старого курса.
Соотношения, связывающие между собой эти величины, ясны из рисунка слева.
 Угол поворота a — разность нового и первоначального курсов:
Угол поворота a — разность нового и первоначального курсов:
Треугольник ВСМ, как образованный двумя касательными и хордой, соединяющей точки касания, является равнобедренным; следовательно, < СВМ = < СМВ = q. (< - это угол). Угол a, как внешний угол треугольника, равен сумме двух внутренних углов:
a = 2q, откуда q = a / 2. (157)
Следовательно, Кср = ИК1 ± q = ИК1 ± a / 2.
Из прямоугольного треугольника ВFО
BF = d / 2 = Rц sin a / 2.
Следовательно,
d = 2Rц sin a / 2. (159)
Дата добавления: 2015-06-22; просмотров: 2271;
