Формула Тейлора для функции многих переменных. Экстремум функции нескольких переменных. Необходимое условие экстремума. Достаточное условие экстремума.

Как известно, функцию F(T) при условии существования ее производных по порядок N+1 можно разложить по формуле Тейлора с остаточным членом в форме Лагранжа. Запишем эту формулу в дифференциальной форме:

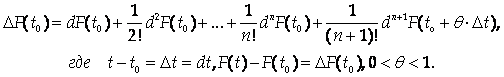
В этой форме формулу Тейлора можно распространить на случай функции нескольких переменных.

Рассмотрим функцию двух переменных F(X, Y), имеющую в окрестности точки (Х0 , у0) непрерывные производные по (N + 1)-й порядок включительно. Зададим аргументам Х И У некоторые приращения DХ и DУ и рассмотрим новую независимую переменную T:

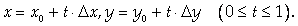
Эти формулы задают прямолинейный отрезок, соединяющий точки (Х0 ,у0) и (Х0+DХ, у0+DУ). Тогда вместо приращения DF(X0,Y0) можно рассматривать приращение вспомогательной функции

F(T) = F(X0+T DX, Y0+TDY),

Равное DF(0) = F(1) – F(0). Но F (T) является функцией одной переменной T, следовательно, к ней применима формула, приведенная в начале раздела. Получаем:

Отметим, что при Линейной замене переменных дифференциалы высших порядков обладают свойством инвариантности, то есть

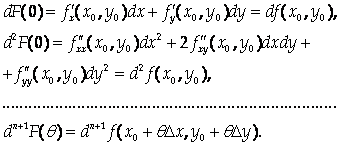
Подставив эти выражения в предыдущую формулу, получим Формулу Тейлора для функции двух переменных:

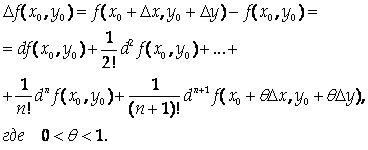
Замечание. В дифференциальной форме формула Тейлора для случая нескольких переменных выглядит достаточно просто, однако в развернутом виде она весьма громоздка. Например, даже для функции двух переменных первые ее члена выглядят так:

Максимум и минимум функции нескольких переменных

Напомним, что под окрестностью точки плоскости понимается внутренность любого прямоугольника, окружающего эту точку, исключая саму точку (проколотая окрестность).

В пространстве это будет произвольный параллелепипед, содержащий эту точку за вычетом самой точки.

Определение. Максимумом (строгим) функции f (x, y) называется такое значение f(x1, y1) этой функции, которое больше всех ее значений f(x, y), принимаемых данной функцией в точках некоторой окрестности точки О(х1, у1). (Окрестность может быть весьма малой по своим линейным размерам).

Определение. Минимумом (строгим) функции f (x, y) называется такое значение f (x2,y2), которое меньше всех ее значений f (x,y), принимаемых данной функцией в точках некоторой окрестности О (х2, у2).

Максимум или минимум функции f (x, y) называется экстремумом этой функции. Точка, в которой достигается экстремум, называется точкой экстремума (точка минимума, точка максимума).

Аналогично определяется экстремум функции f (x, y, z) и т.д.

Теорема. (Необходимый признак экстремума функции нескольких переменных). В точке экстремума функции нескольких переменных каждая ее частная производная первого порядка либо равна нулю, либо не существует.

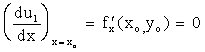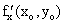Д о к а з а т е л ь с т в о. Пусть u = f (x, y) и f (xo, yo) - ее максимум (для минимума рассуждения аналогичны). Зафиксируем одну из переменных, например, у, полагая у = уо, тогда получим функцию одной переменной U1 = f (x, yo), которая, очевидно, будет иметь максимум при х = хо. Отсюда, на основании теории экстремума одной переменной, получаем, что или не существует.

Пусть теперь у=уо, а хо- фиксируем, тогда 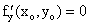или не существует.

С л е д с т в и е. В точке экстремума Мо (хо, уо) дифференцируемой функции f (x, y) выполнены равенства

Для U = f(x, y, z) в точке Мо (хо ,уо, zо) будет выполнено условие .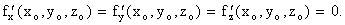

З а м е ч а н и е. Точку, в которой частные производные первого порядка либо не существуют, либо равны нулю, называют критической.

Т.е. экстремумы функции нескольких переменных могут достигаться лишь в критических точках.

Пример. Покажем, что указанные выше условия не являются достаточными. Пусть z = f(x, y) = x × y тогда имеем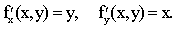

Следовательно, 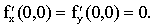Однако точка 0(0,0) не является точкой экстремума, т.к. в любой окрестности точки (о,о) имеются точки

A (e,e) и B(- e, e) " e > :

f(A) = e2 > = f(0) и f(B) = - e2 < f(0).

Абсолютный экстремум

Определение. Наименьшее или наибольшее значение функции в данной области называется абсолютным экстремумом функции. (Соответственно, абсолютный минимум, абсолютный максимум).

Теорема. (Вайерштрасс) Функция, непрерывная в ограниченной и замкнутой области, достигает в этой области своего наименьшего и своего наибольшего значения. (Без доказательства)

Теорема . Абсолютный экстремум функции в данной области достигается либо в критической точке функции, принадлежащей этой области, либо в граничной точке области. (Без доказательства)

Пример. Для функции z = x × y найти абсолютный экстремум в треугольной области S с вершинами О(0,0), А(1,0), В(0,2).

Определим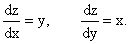

Рис. 15.1.

Критическая точка O(0,0) Î S. На участке ОА имеем у = 0 (0 £ х £ 1) и тогда z = 0.

Аналогично ОВ: х = 0 (0 £ у £ 2) Þ z = 0.

Наконец, отрезок АВ имеет уравнение 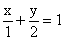или у = 2 - 2х (0 £ х £ 1).

Отсюда z = x × y = 2x - 2x2 .

Имеем 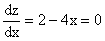, т.е. при 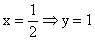и т.к. 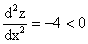, то в точке 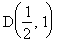функция Z достигает своего наибольшего значения на отрезке АВ.

Итак, наименьшее значение z в S есть m=0 и оно реализуется в точках отрезков ОВ и ОА, составляющих часть границы Г. достигает в точке

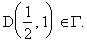
Теорема. (достаточное условие экстремума) Если 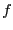дважды дифференцируема в стационарной точке 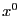, то -- то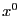чка минимума (максимума), если квадратичная форма 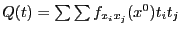положительно (отрицательно) определена. Если эта форма не определена, то экстремума в этой точке нет. Если она вырождена, то неизвестно, является ли 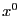точкой экстремума.

Доказательство. По формуле Тейлора приращение функции в точке 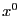можно записать в виде , поскольку, по необходимому условию экстремума, частные производные будут равны нулю. Перепишем выражение в виде 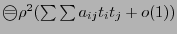, причем 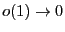при 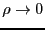. Заметим, что новые переменные 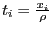изменяются на единичной сфере, т.к. . Кроме того, квадратичная форма 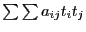непрерывна и по теореме Вейерштрасса на сфере принимает наименьшее значение, обозначим его 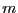. Пусть форма положительно определена. Тогда 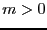. Теперь благодаря тому, что 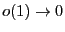при 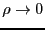можно подобрать такое 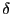, что при 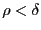выполнено 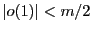, тогда выполнено 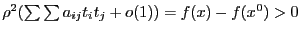в этой окрестности. Что и означает, что 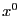-- точка минимума. Для точки максимума доказательство аналогично.

Замечание . В случае двух переменных матрица квадратичной формы имеет вид 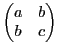. Тогда если 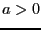, то для положительной определенности достаточно 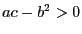-- тогда имеется минимум. Если же 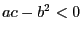, то достигается максимум. Если же , то ничего сказать нельзя.