Двойной интеграл и его свойства. Сведение двойного интеграла к повторному.
 Определение двойного интеграла. Пусть на плоскости XY задана функция
Определение двойного интеграла. Пусть на плоскости XY задана функция 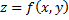 и область (P) (область задания функции f(x,y)), её площадь P. Произведём разбиение площади сеткой кривых Pi, где Pi – частичная область. Внутри частичной области возьмём произвольную точку с координатами (ξi,ηi). Составим интегральную сумму:
и область (P) (область задания функции f(x,y)), её площадь P. Произведём разбиение площади сеткой кривых Pi, где Pi – частичная область. Внутри частичной области возьмём произвольную точку с координатами (ξi,ηi). Составим интегральную сумму: 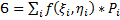 . Пусть λ – характеристика разбиения, которая равна
. Пусть λ – характеристика разбиения, которая равна 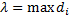 , где di – диаметр частичной области. Диаметр – максимальное расстояние между любой парой точек в области. Устремим λ к нулю. Если существует предел интегральных сумм
, где di – диаметр частичной области. Диаметр – максимальное расстояние между любой парой точек в области. Устремим λ к нулю. Если существует предел интегральных сумм 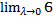 , то этот предел и называется двойным интегралом:
, то этот предел и называется двойным интегралом: 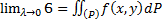 .
.
Основные свойства двойного интеграла:
Свойство аддитивности: 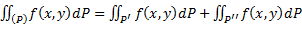
Свойства линейности:
а) 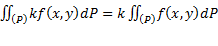
б) 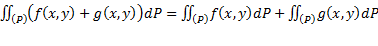
Модуль интеграла меньше или равен интегралу от модуля:
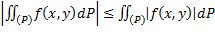
Теорема о среднем. Так как
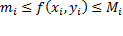
то, проинтегрировав это неравенство, получим:
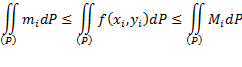
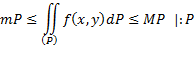
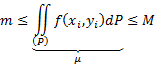
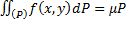
Где
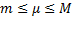
Сведение двойного интеграла к повторному.
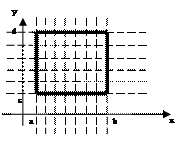 Теорема. Если функция f(x, y) интегрируема в прямоугольнике, указанном на рисунке, и если
Теорема. Если функция f(x, y) интегрируема в прямоугольнике, указанном на рисунке, и если 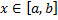 и существует интеграл
и существует интеграл 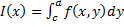 , тогда существует повторный интеграл
, тогда существует повторный интеграл 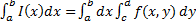 и он равен двойному:
и он равен двойному: 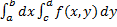 =
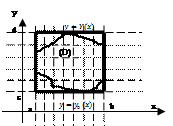
= 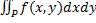 .
.
 Замечание. Если f(x, y) интегрируема в прямоугольнике, указанном на рисунке, и
Замечание. Если f(x, y) интегрируема в прямоугольнике, указанном на рисунке, и 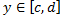 и существует интеграл
и существует интеграл 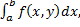 тогда существует повторный интеграл
тогда существует повторный интеграл 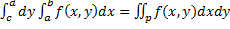 .
.
Предположим, что область D произвольного вида. Делаем разбиение и проводим параллельные линии. Заключим область (D) в прямоугольник (D*), 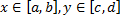 , и в нём определим функцию f*(x,y):
, и в нём определим функцию f*(x,y): 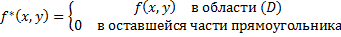 .
. 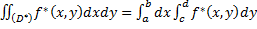
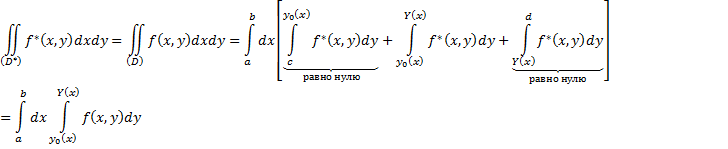
Формула в общем виде: 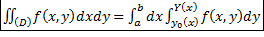 . Так же доказывается, что
. Так же доказывается, что 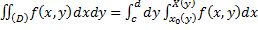
Тройной интеграл, сведение его к повторному.
 Определение тройного интеграла. Пусть в некоторой области (V) с границей (S) задана в каждой точке функция f(x,y,z). Разобьём тело (V) сеткой поверхностей на частичные области (Vi). В каждой (Vi) возьмём произвольную точку (ξi, ηi, ζi) и составим интегральную сумму:
Определение тройного интеграла. Пусть в некоторой области (V) с границей (S) задана в каждой точке функция f(x,y,z). Разобьём тело (V) сеткой поверхностей на частичные области (Vi). В каждой (Vi) возьмём произвольную точку (ξi, ηi, ζi) и составим интегральную сумму: 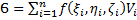 . Устремим максимальный диаметр (макс. расстояние между любой парой точек в области) к нулю:
. Устремим максимальный диаметр (макс. расстояние между любой парой точек в области) к нулю: 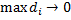 . Тогда, если существует предел интегральных сумм, то он равен тройному интегралу:
. Тогда, если существует предел интегральных сумм, то он равен тройному интегралу: 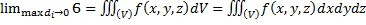 .
.
На всякий случай определение интегральной суммы. Пусть на нек-ом отрезке 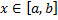 задана
задана 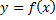 . Произведём разбиение отрезка:
. Произведём разбиение отрезка: 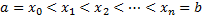 . Число
. Число 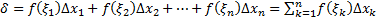 , называется интегральной суммой функции f(x), соответствующей данному разбиению T(ξi;xi) сегмента [a;b] и данному выбору промежуточных точек ξi на частичных сегментах [xi-1;xi], Δ –хар-тика разбиения:
, называется интегральной суммой функции f(x), соответствующей данному разбиению T(ξi;xi) сегмента [a;b] и данному выбору промежуточных точек ξi на частичных сегментах [xi-1;xi], Δ –хар-тика разбиения: 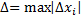
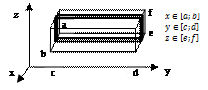 Сведение к повторному интегралу. Рассмотрим первый простейший случай. Пусть тело V – прямоугольный параллелепипед. Проведём секущую плоскость. Возьмём приращение плоскости (жирные линии). Тогда:
Сведение к повторному интегралу. Рассмотрим первый простейший случай. Пусть тело V – прямоугольный параллелепипед. Проведём секущую плоскость. Возьмём приращение плоскости (жирные линии). Тогда: 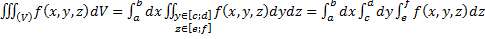 .
.
 Рассмотрим второй случай.
Рассмотрим второй случай.
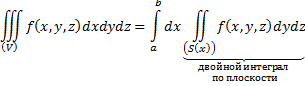
 Рассмотрим третий случай – область (V) цилиндрического типа.
Рассмотрим третий случай – область (V) цилиндрического типа.
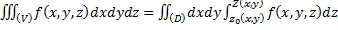
26. Замена переменных в двойном интеграле. Пример: случай полярных координат.
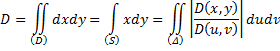
Вычислим интеграл 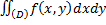 , используя замену переменных
, используя замену переменных 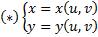 . Рассмотрим интеграл как предел интегральных сумм. Область (D) сеткой кривых разделяется на частичные области Di, внутри каждой частичной области берём произвольные точки (xi, yi). Составляем интегральную сумму:
. Рассмотрим интеграл как предел интегральных сумм. Область (D) сеткой кривых разделяется на частичные области Di, внутри каждой частичной области берём произвольные точки (xi, yi). Составляем интегральную сумму: 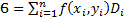 , где Di – площадь i-ой частичной области. Устремим максимальный диаметр к нулю:
, где Di – площадь i-ой частичной области. Устремим максимальный диаметр к нулю: 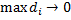 . По определению,
. По определению, 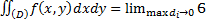 . Совершим замену переменных (*). При замене (*) площадь
. Совершим замену переменных (*). При замене (*) площадь 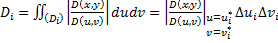 .
.
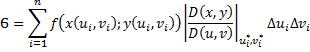
Если 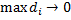 , то
, то 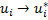 и
и 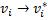 , следовательно,
, следовательно, 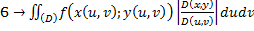
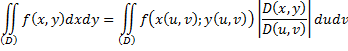
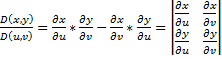 – якобиан преобразования (*).
– якобиан преобразования (*).
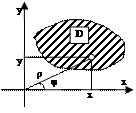 Пример с полярными координатами.
Пример с полярными координатами. 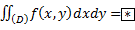
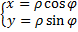
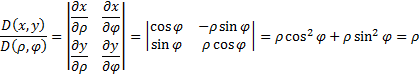
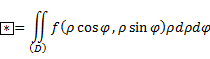
Дата добавления: 2015-05-16; просмотров: 4292;
