Определение криволинейных интегралов первого и второго рода, их основные свойства и вычисление.
 Определение криволинейного интеграла первого рода, его основные свойства и вычисление.
Определение криволинейного интеграла первого рода, его основные свойства и вычисление.
Кривая должна быть простой кривой, то есть 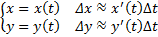 .
.
Пусть кривая будет разбита точками разбиения. Составим интегральную сумму.

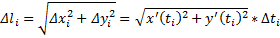



Полученный интеграл называется криволинейным интегралом первого рода.
На словах можно сказать так. Если существует предел интегральной суммы (см. выше) при стремлении к нулю наибольшей из длин Δlk (то есть  ), то этот предел называется криволинейным интегралом первого рода от функции f(x,y) по кривой L и обозначается символом
), то этот предел называется криволинейным интегралом первого рода от функции f(x,y) по кривой L и обозначается символом  или
или  .
.
Если кривая задана не параметрически, а, к примеру, так: 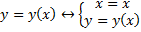 , тогда
, тогда  .
.
Основные свойства:
Линейность: 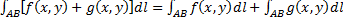
Аддитивность (если дуга AB составлена из двух дуг AC и CB): 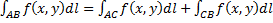
Монотонность: если f<=g на L, то: 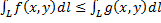
Изменение направления обхода кривой интегрирования не влияет на знак: 
Оценка модуля интеграла: 
Вычисление. Пусть L – кривая, как на рисунке, заданная параметрически. Пусть функция f(x,y) определена и интегрируема вдоль кривой l как криволинейный интеграл первого рода. Тогда:  .
.
Таким образом, для вычисления по длине дуги АВ надо, используя параметрическое уравнение кривой, выразить подынтегральную функцию через параметр t, заменить dl дифференциалом дуги в зависимости от параметра t и проинтегрировать полученное выражение по t.
Определение криволинейного интеграла второго рода, его основные свойства и вычисление. Связь с интегралом первого рода.
 Пусть кривая L на координатной плоскости Оху задана параметрически уравнениями
Пусть кривая L на координатной плоскости Оху задана параметрически уравнениями 
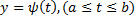 . L называется простой (плоской) незамкнутой кривой, если функции
. L называется простой (плоской) незамкнутой кривой, если функции 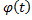 ,
, 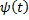 непрерывны на
непрерывны на 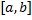 и различным значениям параметра t из сегмента
и различным значениям параметра t из сегмента 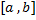 соответствуют различные точки
соответствуют различные точки  ,
, 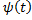 . Если точка
. Если точка  совпадает с точкой
совпадает с точкой 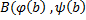 , а остальные точки не являются кратными, то L называется простой замкнутой кривой. Простая кривая L называется спрямляемой, если существует предел (длинa кривой L) длин ломаных, вписанных в кривую, при Δt → 0.
, а остальные точки не являются кратными, то L называется простой замкнутой кривой. Простая кривая L называется спрямляемой, если существует предел (длинa кривой L) длин ломаных, вписанных в кривую, при Δt → 0.
Пусть на кривой AB заданы две функции, P(x, y) и Q(x, y). Разобьем сегмент 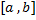 на n частей точками
на n частей точками 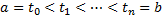 . Кривая АВ разобьется на n частей точками
. Кривая АВ разобьется на n частей точками 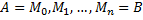 в направлении от A к B. Пусть
в направлении от A к B. Пусть 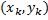 – координаты точки
– координаты точки 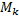 ,
, 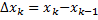 ,
, 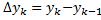 ,
, 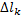 – длина дуги
– длина дуги 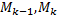 . На каждой дуге
. На каждой дуге 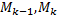 возьмем некоторую точку (координаты
возьмем некоторую точку (координаты 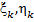 ) и составим две интегральные суммы:
) и составим две интегральные суммы:  ,
,  . Если существует предел интегральной суммы
. Если существует предел интегральной суммы 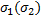 при стремлении к нулю наибольшей из длин
при стремлении к нулю наибольшей из длин 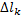 , то этот предел называется криволинейным интегралом второго рода
, то этот предел называется криволинейным интегралом второго рода  . Сумма
. Сумма 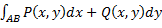 называется общим криволинейным интегралом второго рода.
называется общим криволинейным интегралом второго рода.
Из определения криволинейного интеграла второго рода следует, что при изменении направления обхода кривой AB изменяется и знак интеграла 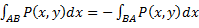 . Аналогично вводится
. Аналогично вводится  для пространственной кривой, заданной параметрически
для пространственной кривой, заданной параметрически 

Криволинейные интегралы обладают теми же свойствами, что и обычные определенные: Линейность  . Аддитивность:
. Аддитивность:  . Монотонность: если f
. Монотонность: если f  g, то
g, то  .
.
Кривая L кусочно-гладкая, если она непрерывна и распадается на конечное число не имеющих общих внутренних точек кусков, каждый из которых представляет собой гладкую кривую.
Вычисление криволинейного интеграла второго рода с помощью определенного интеграла.
Если AB – кусочно-гладкая кривая, а функции Р=Р(x,y) и Q=Q(x,y) кусочно непрерывны вдоль кривой AB, то справедливо равенство: 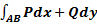 =
=  .
.
Если кривая AB задана уравнением y = у(x), a≤x≤b, и имеет кусочно-непрерывную производную, а функции P(x,y) и Q(x,y) кусочно непрерывны вдоль кривой AB, то имеет место равенство: 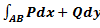 =
=  .
.
Связь между криволинейными интегралами первого и второго рода.
Пусть AB− кусочно гладкая кривая, функции Р=P(x,y) и Q=Q(x,y) кусочно непрерывны вдоль кривой AB и 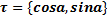 − единичный касательный вектор к кривой AB в точке M(x,y), причем направление
− единичный касательный вектор к кривой AB в точке M(x,y), причем направление  соответствует направлению движения от А к В (α − угол между вектором
соответствует направлению движения от А к В (α − угол между вектором 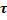 в точке M(x, y) и осью Oх).
в точке M(x, y) и осью Oх).  . Для пространственной кривой справедлива аналогичная теорема:
. Для пространственной кривой справедлива аналогичная теорема: 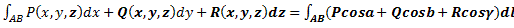 .
.
Из лекций: 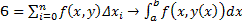
Это и есть криволинейный интеграл второго рода.
 – то же самое, только по y.
– то же самое, только по y.
Каждый интеграл второго рода может быть сведён к первому роду.

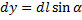
 или
или 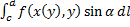
Дата добавления: 2015-05-16; просмотров: 1799;
