Предел функции нескольких переменных. Непрерывность функции. Частные производные.

Определение. Число А называется пределом функции f(M), где М(x1,x2,…xn) – точка n-мерного пространства, при стремлении точки М к точке М0(x10,x20,…xn0) любым образом, если для всякого сколь угодно малого 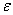>0 существует такое число 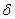>0, что из условия < 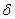, где - расстояние между точками М и М0, следует < .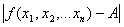

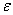Обозначается:

А .

Пусть z=f(x,y). Придадим x и y приращения и 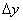. Получим приращение функции z=f(x,y). Если

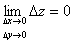, (1)

т.е. бесконечно малым аргументам соответствует бесконечно малое приращение функции, то говорят, что функция непрерывна.

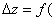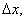Распишем x0+ y+ 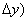-f(x0,y0) и положим x0+ x=x,y0+ 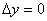,то выражение(1) можно записать в виде

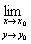f(x,y)=f(x 0,y0), (2)

т.е. непрерывность функции означает, что ее предел равен ее значению от пределов аргументов.

Функция, непрерывная в каждой точке некоторой области, называется непрерывной в области. Если в некоторой точке не выполняется условие (2), то эта точка называется точкой разрыва.

Частные производные.

Пусть z=f(x,y). Зафиксируем какую-либо точку (x,y), а затем, не меняя закрепленного значения аргумента y, придадим аргументу x приращение . Тогда z получит приращение, которое называется частным приращением z по x и обозначается 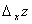и определяется формулой .

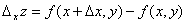Аналогично, если x сохраняет постоянное значение, а y получает приращение 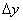, то z получает частное приращение z по y, .

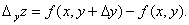Определение. Частной производной по x от функции z=f(x,y) называется предел отношения частного приращения 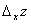по x к приращению при стремлении к нулю, т.е.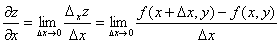

Частная производная обозначается одним из символов .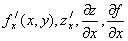

Аналогично определяется частная производная по y:

.

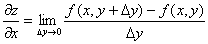Таким образом, частные производные функции двух переменных вычисляются по тем же правилам, что и производные функции одного переменного.

Пример. Найти частные производные функции z=x2e x-2y.

Решение.

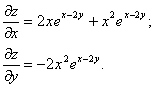
Частные производные функции любого числа переменных определяются аналогично.

4. Геометрическая интерпретация частных

производных функции двух переменных

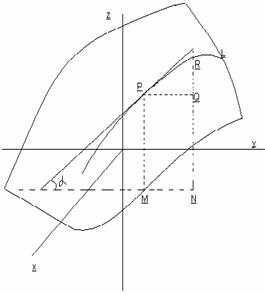
Пусть уравнение z=f(x,y) –это уравнение поверхности. Проведем плоскость x=const. L- линия пересечения поверхности с плоскостью x=const. При данном x на плоскости ХОУ возьмем точку М. На поверхности z=f(x,y) ей соответствует точка Р(x,y,z). Дадим переменному y приращение 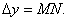Тогда функция z получит приращение 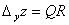Отношение 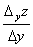равно тангенсу угла, образованного секущей RР с положительным направлением оси ОУ,

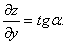
Итак, частная производная 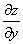численно равна тангенсу угла

наклона касательной к кривой, получающейся в сечении поверхности z=f(x,y) плоскостью x=const.

Аналогично, частная производная 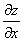численно равна тангенсу угла наклона касательной к кривой, получающейся в сечении поверхности z=f(x,y) плоскостью x=const.