Признак Вейерштрасса равномерной сходимости.

Признак Вейерштрасса:

Если числовой ряд с неотрицательными членами 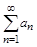сходится и для членов функционального ряда при всех и всех справедливы оценки

,

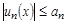то ряд сходится абсолютно и равномерно в области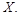

Говорят в этом случае, что числовой ряд 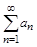«мажорирует» исходный функциональный ряд, а сам числовой ряд называют мажорантным.

Существует простой признак для проверки равномерной сходимости(принак Вейерштрасса)

Можно рассматривать 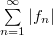и при этом сохраняется терминология числовых рядов, связанная с абсолютной и условной сходимостью.

Как и в рядах, абсолютная сходимость сильнее сходимости: из абсолютной сходимости вытекает сходимость.

Теорема (Вейерштрасс):

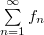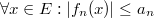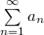, , — сходится. Тогда 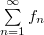равномерно сходится на .

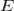Доказательство:

Применим критерий Коши:

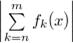
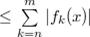
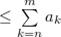
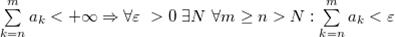
Сопоставляя с предыдущим неравенством, которое верно ,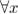

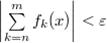. Тогда, по критерию Коши, ряд равномерно сходится.

Свойства равномерно сходящихся функциональных рядов. Теорема о непрерывности суммы равномерно сходящегося ряда из непрерывных функций. Теорема о почленном интегрировании и дифференцировании ряда (без доказательства).

Общие свойства функциональных рядов

О п р е д е л е н и е. Ряды

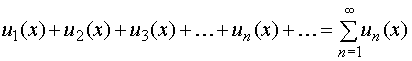, (24)

члены которых являются функциями от х, называются функциональными. Предполагается, что все функции u_n(x) определены и непрерывны в одном и том же интервале, конечном или бесконечном.

Ряд (24) может сходиться для одних значений х и расходиться для других. Значение х = х₀, при котором получающийся из (24) числовой ряд

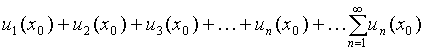(25)

сходится, называется точкой сходимости ряда (24). Совокупность всех точек сходимости ряда называется областью сходимости ряда. Областью сходимости функционального ряда обычно бывает какой-нибудь промежуток оси Ох. Говорят, что ряд (24) сходится в этой области.

Сумму n первых членов ряда (n-ю частичную сумму) обозначают через S_n(x) , а остаток ряда обозначают через R_n(x). Функциональный ряд сходится при некотором значении х, если существует конечный предел

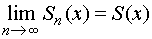и .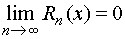

S(x) – сумма функционального ряда. Ее можно представить в виде S(x) = S_n(x) + R_n(x). Каждому значению х из области сходимости Х соответствует определенное значение S(x).

Равномерная сходимость ряда

О п р е д е л е н и е. Функциональный ряд (24) называется равномерно сходящимся в некоторой области Х, если для любого сколь угодно малого числа 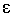> 0 можно указать такое целое число N( 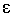) > 0, зависящее только от e и не зависящее от х, что при всех n > N( 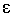) неравенство 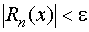выполняется для всех х из области Х.

Достаточный признак равномерной сходимости функционального ряда – признак Вейерштрасса

Если члены функционального ряда (24) u₁(x), u₂(x),u₃(x),…, u_n(x)… в некоторой области Х по абсолютной величине не превосходят соответствующих членов некоторого сходящегося числового ряда с положительными членами 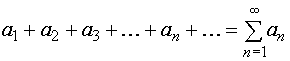, то функциональный ряд

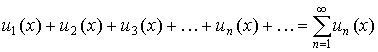
в этой области сходится равномерно.

Это значит, что во всех точках области Х должно выполняться неравенство 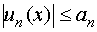, (n = 1, 2, 3, …). Ряд 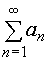называется мажорантным (усиливающим) по отношению к ряду (24).

Свойства равномерно сходящихся функциональных рядов

1. Сумма S(x) равномерно сходящегося ряда 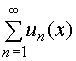в области Х, где u_n(x) (n = 1, 2, 3, …) - непрерывные функции, является непрерывной функцией в области Х.

2. Равномерно сходящийся ряд 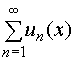, где u_n(x) (n = 1, 2, 3, …) -непрерывные функции, можно почленно интегрировать, т.е. справедливо равенство

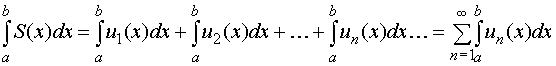. (26)

3. Если ряд

,

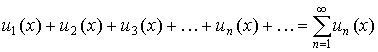составленный из функций, имеющих непрерывные производные , сходится в области C и его сумма равна S(x), а ряд из производных 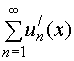сходится в этой области равномерно, то производная суммы ряда 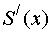равна сумме ряда из производных:

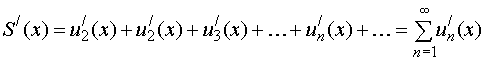. (27)

Коротко эту теорему формулируют так:

Если ряд, составленный из производных сходящегося ряда (27), сходится равномерно, то исходный ряд (24) можно почленно дифференцировать.

Отметим: здесь не предполагаются равномерная сходимость исходного ряда, а также дифференцируемость его суммы; они следуют из условий теоремы. Однако проверка равномерной сходимости ряда 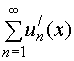является обязательной; при невыполнении этого теорема может потерять смысл (т.е. оказаться неприменимой).