Функциональный ряд. Сумма ряда. Определение равномерной сходимости ряда. Критерий Коши равномерной сходимости функционального ряда.

Определение. Ряд, члены которого являются функциями, называется функциональным рядом. Его обозначают:

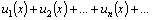
(1)

Определение. Если при ряд (1) сходится, то называется точкой сходимости ряда (1).

Определение. Множество всех значений 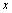, при которых функциональный ряд сходится, называется областью сходимости этого ряда.

Очевидно, что в области сходимости функционального ряда его сумма является функцией от 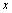. Будем ее обозначать .

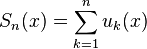— n-ная частичная сумма.

Ряд называется сходящимся равномерно, если последовательность 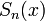его частичных сумм сходится равномерно.

Функциональный ряд называется равномерно сходящимся в некоторой области Х, если для любого сколь угодно малого числа > 0 можно указать такое целое число N( ) > 0, зависящее только от e и не зависящее от х, что при всех n > N( ) неравенство выполняется для всех х из области Х.

Свойства равномерно сходящихся рядов.

1. Сумма S(x) равномерно сходящегося ряда 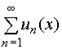в области Х, где un(x) (n = 1, 2, 3, …) - непрерывные функции, является непрерывной функцией в области Х.

2. Равномерно сходящийся ряд , где un(x) (n = 1, 2, 3, …) -непрерывные функции, можно почленно интегрировать, т.е. справедливо равенство

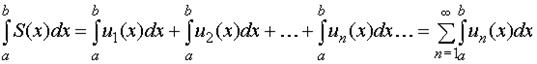. (26)

3. Если ряд

,

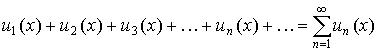составленный из функций, имеющих непрерывные производные 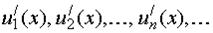, сходится в области C и его сумма равна S(x), а ряд из производных 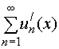сходится в этой области равномерно, то производная суммы ряда 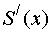равна сумме ряда из производных:

. (27)

Определение. Частными (частичными) суммами функционального ряда 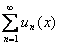называются функции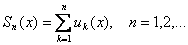

Определение. Функциональный ряд 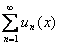называется сходящимся в точке (х=х0), если в этой точке сходится последовательность его частных сумм. Предел последовательности 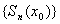называется суммой ряда 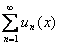в точке х0.

Определение. Совокупность всех значений х, для которых сходится ряд 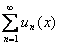называется областью сходимости ряда.

Определение. Ряд 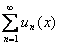называется равномерно сходящимся на отрезке [a,b], если равномерно сходится на этом отрезке последовательность частных сумм этого ряда.

Теорема. (Критерий Коши равномерной сходимости ряда)

Для равномерной сходимости ряда 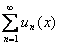необходимо и достаточно, чтобы для любого числа e>0 существовал такой номер N(e), что при n>N и любом целом p>0 неравенство

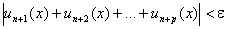
выполнялось бы для всех х на отрезке [a,b].