Волны в упругих средах и их виды. Фронт волны, плоские и сферические волны.

Волной принято называть распространение в пространстве изменений какой-либо физической величины. Изменения величины могут носить как периодический, так и непериодический характер. Для того, чтобы эти изменения могли распространяться в некоторой области пространства, необходимо наличие некоторых условий; в частности, в каждой точке рассматриваемой области физическая величина должна иметь определенное значение (принято говорить, что величина имеет полевой характер). Кроме того должна осуществляться взаимосвязь изменения физической величины в одной точке пространства с изменением этой же величины в соседних точках. Скорость распространения изменения определяется как природой изменяемой величины, так и свойствами среды, в которой распространяется это изменение. При этом определенную роль играет направление колебаний в волне. Если направление колебаний совпадает с направлением распространения волны, то такие волны называют продольными. Если же колебания происходят в плоскости, перпендикулярной направлению распространения волны, то такие волны являются поперечными.Если относительное изменение величины (т.е. изменение, деленное на саму величину) мало по сравнению с единицей, то такое изменение называют возмущениемфизической величины. Примером распространения возмущения могут служить волны на поверхности воды, возникающие при бросании в воду камешка. Образовавшиеся искажения поверхности воды (рис.6.1) начнут распространяться во все стороны, образуя своеобразные кольцевые структуры. Возникшая волна достигнет некоторой точки, отстоящей на расстояние х от места попадания камня в воду через время t = 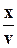, где v - скорость распространения возмущения по поверхности воды.

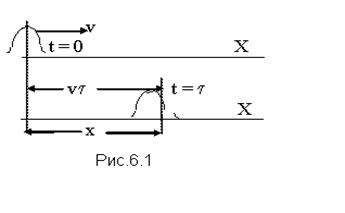
Пусть в точке попадания камня в воду профиль образовавшегося возмущения является некоторой функцией от времени f (t). Ясно, что в любой точке поверхности, куда доходит образовавшееся возмущение, величина f (t) будет зависеть не только от времени, но также и от расстояния, однако для упрощения предположим, что возмущение сохраняет свою форму вне зависимости от пройденного расстояния. Тогда в любой точке поверхности, отстоящей от начальной точки на расстояние х, профиль возмущения f(t) будет изменяться во времени с некоторым запаздыванием на величину t = x/v , т.е. аргументом функции f(t) станет величина (t - х/v). Независимость величины возмущения от координаты означает, что f(t) = f(t - х/v) . Волны, для которых имеет место последнее равенство называются плоскими. Если в начальной точке возмущение изменяется по гармоническому закону, то такая волна называется синусоидальной. Синусоидальная плоская волна записывается в таком виде:

f (х, t) = Аsinw(t - 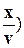= Аsin (wt - 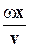) = Asin (wt - kx), (6-1)

где 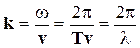- так называемое волновое число, a величина 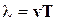называется длиной волны. Аргумент синуса в уравнении (6-1) определяет фазу волны F (x,t). Поверхность, соединяющая все точки, фазы которых одинаковы, называется волновой поверхностью или фронтом волны. Если волна плоская, то фронтом волны является плоская поверхность. Волна, распространяющаяся во все стороны от точечного источника, называется сферической; очевидно, что для такой волны волновая поверхность представляет собой сферу. Если на какой-либо поверхности фаза постоянна, т.е. Ф(x,t) = const, скорость перемещения координаты, для которой фаза постоянна можно определить дифференцируя условие постоянства фазы: 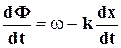= 0 , откуда

v_фаз = 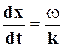, (6-2)

т.е. скорость распространения волны совпадает со скоростью распространения постоянной фазы. Направление колебаний в распространяющейся волне может совпадать с направлением волны - в этом случае волна называется продольной, но может быть и так, что распространение волны происходит в направлении, перпендикулярном плоскости, в которой совершаются колебания; тогда волны называются поперечными. Например, распространение звука - это продольные волны. Примером поперечных волн могут служить волны на поверхности воды.