Формула Бернулли

Определение. Повторные независимые испытания называются испытаниями Бернулли, если каждое испытание имеет только два исхода, и вероятности исходов остаются неизменными для всех испытаний.

Обычно эти две вероятности обозначаются через 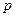и , и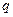сход с вероятностью 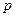называют «успехом» и обозначают символом 1, а второй – «неудачей» и обозначают символом 0. Очевидно, что 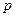и 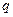должны быть неотрицательными и должно выполняться равенство

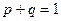. (4.1.1)

Пространство элементарных исходов каждого отдельного испытания состоит из двух исходов 1 и 0. Очевидно, пространство элементарных исходов 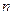испытаний Бернулли содержит 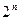последовательностей из 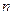символов 1 и 0. Так как испытания независимы, то вероятности перемножаются, т. е. вероятность любой конкретной последовательности есть произведение, полученное при замене символов 1 и 0 вероятности на 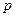и 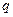соответственно. Таким образом, вероятность исхода 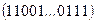равна:

.

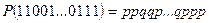Но на практике нас, как правило, интересует не порядок появления успехов в последовательности 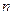испытаний Бернулли, а их общее число.

Теорема. Вероятность 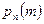того, что в 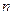испытаниях Бернулли число успехов равно 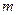, вычисляется по формуле

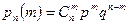, (4.1.2)

где 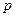— вероятность «успеха», а 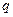— вероятность «неудачи».

Доказательство. Событие «в 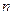испытаниях Бернулли число успехов равно 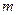и число неудач — 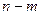» содержит столько элементарных исходов, сколько существует способов размещения 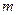символов на 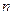местах, т.е. 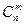. А так как вероятность конкретной последовательности, содержащей 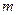символов 1, равна 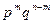,то в итоге получаем:

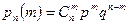. n

Число успехов в 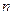испытаниях обозначают через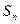, тогда 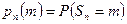. Очевидно, что 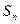есть случайная величина, а функция (4.1.2) является «распределением» этой случайной величины. Будем называть это распределение биномиальным. Слово биномиальное отражает тот факт, что (4.1.2) представляет собой m-й член биноминального разложения 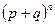. Отсюда следует, что

.

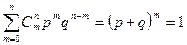Пример 1. Стрелок попадает в мишень с вероятностью 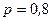. Найти вероятность того, что в результате пяти независимых выстрелов стрелок попадает:

a) ровно четыре раза;

б) не менее трех раз.

m Решение. Для решения данной задачи применим формулу (4.1.2), в которой:

.

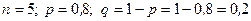а) Число успехов равно 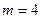. Таким образом, искомая вероятность:

.

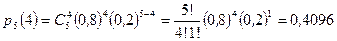б) Обозначим 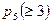— вероятность попадания не менее трех раз из пяти.

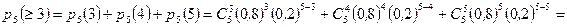
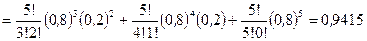. l

Пример 2.Сколько испытаний с вероятностью успеха 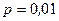нужно произвести, чтобы вероятность хотя бы одного успеха была не меньше 0,5?

m Решение. Рассмотрим следующие события:

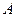— в схеме Бернулли наблюдался хотя бы один успех;

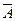— в схеме Бернулли не наблюдалось ни одного успеха.

Для решения задачи используем формулу (4.1.2), согласно которой вероятность того, что успехов не будет (т.е. число успехов равно нулю), равна:

.

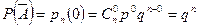Используя свойство вероятности противоположного события, получаем, что вероятность того, что будет хотя бы один успех, равна:

.

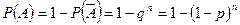Остается найти наименьшее целое 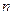, для которого выполнено неравенство:

.

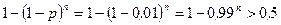Решим последнее неравенство.

.

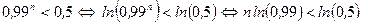Разделив последнее неравенство на 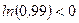, получим

.

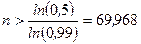Наименьшим целым числом 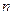, удовлетворяющим последнему неравенству, является 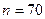. l

Пример 3.Что вероятнее выиграть у равносильного противника (ничейный исход партии исключен):

а) три партии из четырех или пять из восьми;

б) не менее трех партий из четырех или не менее пяти партий из восьми.

m Решение. Так как противники равносильны и ничейный исход партии исключен, то вероятности выигрыша и проигрыша каждой партии одинаковы и .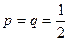

а) Вероятность выигрыша трех партий из четырех равна:

,

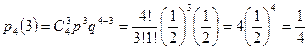а вероятность выигрыша пяти партий из восьми равна:

.

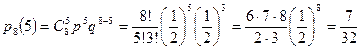Так как 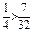, то вероятнее выиграть три партии из четырех.

б) Вероятность выигрыша не менее трех партий из четырех равна:

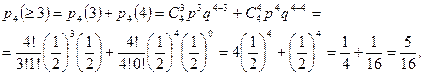
а вероятность выигрыша не менее пяти партий из восьми равна:

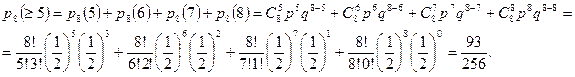
Так как 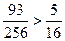, то вероятнее выиграть не менее пяти партий из восьми. l