Условная вероятность

Рассмотрим следующий пример. Бросаются две игральные кости. Найдем вероятность того, что сумма выпавших очков равна 8, если заранее известно, что сумма выпавших очков есть четное число. Всевозможные исходы запишем в виде таблицы 3.1:

Таблица 3.1

Из таблицы видно, что число всевозможных исходов равно 36, но число исходов, удовлетворяющих условию, при которых сумма очков есть четное число, равно 18. Из них ровно в 5 исходах сумма очков равна 8. Пользуясь классическим определением вероятности, находим, что искомая вероятность равна .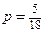

Заметим, что безусловная вероятность того, что сумма выпавших очков, равная 8, равна 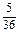, т.е. задание дополнительного условия может повлиять на вычисление вероятности.

Найдем условную вероятность 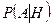события при условии, что событие 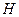уже произошло. Для простоты рассмотрим классическую схему. Естественно положить, что данная вероятность есть отношение числа исходов 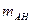, благоприятных совместному (одновременному) осуществлению событий и 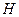, к числу исходов, благоприятных событию 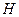, т.е.

.

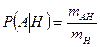Разделив числитель и знаменатель на число всевозможных исходов , получим:

.

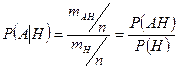Последняя формула может служить общим определением условной вероятности при аксиоматическом подходе.

Определение. Условной вероятностью 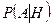события при условии, что событие уже произошло, называется отношение вероятности совместного (одновременного) осуществления событий и 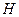к вероятности события :

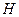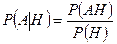. (3.1.1)

Пример 1. При трехкратном подбрасывании монеты выпало два «герба». Найти условную вероятность того, что при втором подбрасывании выпал «герб».

m Решение. Рассмотрим следующие события:

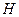— при трехкратном подбрасывании выпало два «герба»;

— при втором подбрасывании выпал «герб».

Событию 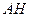соответствует два исхода: Г – Г – Р, Р – Г – Г.

Число всевозможных исходов при трехкратном подбрасывании монеты 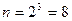. Отсюда находим:

.

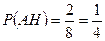Аналогично, событию 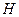соответствует три исхода, следовательно, вероятность условия равна

.

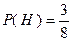Далее, применяя (3.1.1), получаем искомую вероятность

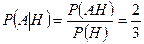. l