Классическое определение вероятности

Рассмотрим опыт с бросанием монеты. Пространство элементных исходов 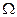содержит два элементарных исхода:

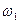— появление «герба»;

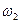— появление «решки».

В силу того, что монета симметрична, нельзя предпочесть «герб» «решке» (или наоборот). Следовательно, обоим элементарным исходам необходимо сопоставить одинаковую вероятность . Далее очевидно, что

.

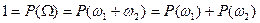Откуда получаем:

.

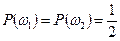Рассмотрим общий случай. Пусть пространство 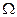состоит из 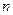всевозможных равнозначных исходов . Теперь каждому элементарному исходу поставим в соответствие вероятность .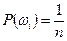

Далее рассмотрим некоторое событие , которому соответствует ровно 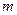(благоприятных) элементарных исходов .

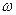Положим

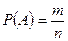. (2.1.1)

Таким образом, в классической схеме вероятность любого события определяется как отношение числа 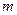благоприятных для события элементарных исходов к общему числу элементарных исходов .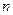

Пример 1. В урне находятся 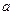белых и 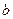черных шаров. Из урны вынимают наугад один шар. Найти вероятность того, что этот шар белый (событие ).

m Решение.Число всевозможных исходов равно

.

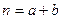Число благоприятных исходов равно

.

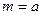Таким образом, используя классическое определение вероятности, получаем

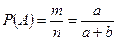. l

Пример 2. Имеются две урны: в первой – 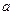белых и 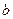черных шаров; во второй – 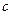белых и 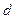черных шаров. Из каждой урны вынимается по шару. Найти вероятность того, что оба шара будут белыми (событие А).

m Решение.Каждый шар из первой урны может комбинировать с каждым шаром из второй урны. Следовательно, число всевозможных исходов:

.

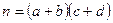Аналогично, число благоприятных исходов:

.

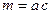Следовательно, используя классическое определение вероятности, получаем:

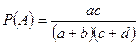. l

Пример 3.Из колоды карт (36 листов) наудачу выбирается одна карта. Определить вероятность того, что она окажется тузом (событие А).

m Решение. Число всевозможных исходов равно:

.

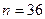Число благоприятных исходов равно числу тузов, т.е.

.

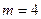Таким образом, используя классическое определение вероятности, получаем:

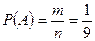. l