Геометрическое определение вероятности

Пусть теперь рассматривается непрерывная вероятностная схема, т.е. пространство элементарных исходов представляет собой некоторую ограниченную область (отрезок, круг, шар и т.д.) k‑мерного пространства (прямой, плоскости, трёхмерного пространства и т.д.). В непрерывном случае число элементарных исходов бесконечно, следовательно, при использовании принципа равновероятности каждому элементарному исходу можно приписать только нулевую вероятность. Поэтому подойдём к определению геометрической вероятности по-другому. Рассмотрим сначала отрезок 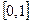и предположим, что идеальная частица равномерно бросается на данный отрезок. Каждому интервалу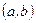 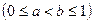поставим в соответствие вероятность попадания частицы на этот интервал, равную его длине: .

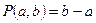В общем случае геометрическая вероятность определяется аналогично. Пусть 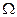— некоторая область, имеющая меру 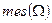(длину, площадь, объём и т.д.) такую, что 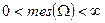. Пусть область находится внутри области .

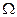Определение. Геометрической вероятностью называют отношение меры области к мере области :

.

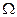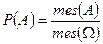Пример 8.(Задача о встрече.) Два лица и 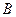договорились встретиться в определённом месте между 12 часами и часом. Пришедший первый ждёт другого в течение 20 минут, после чего уходит. Чему равна вероятность встречи лиц и 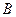, если приход каждого из них в течение указанного часа может произойти на удачу и моменты прихода независимы.

m Решение. Обозначим момент прихода лица через 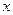, а момент прихода лица 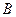через 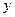. На плоскости; в качестве единицы масштаба выберем минуту. Всевозможные исходы изобразятся точками квадрата со сторонами 60. Для того, чтобы встреча произошла необходимо и достаточно, чтобы выполнялось неравенство .

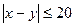Исходы, благоприятствующие встрече, изображены в заштрихованной области (рис. 2.1).

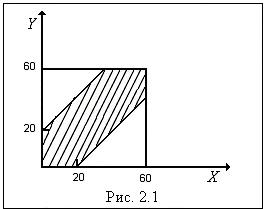
Искомая вероятность равна отношению площади заштрихованной области к площади всего квадрата 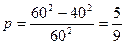. l

Пример 9. В круг радиуса 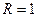случайным образом бросается точка. Найти вероятность того, что точка попадёт в круг радиуса 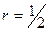с тем же центром (рис. 2.2).

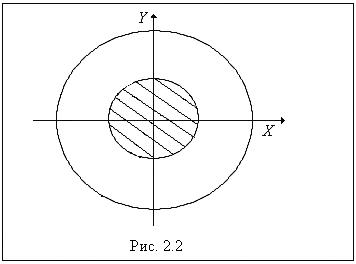
m Решение. Первый способ.

Пусть — событие, состоящее в попадании точки в малый круг. Определим вероятность 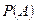как отношение площади малого круга к площади большего:

.

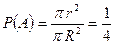Второй способ. Рассмотрим полярную систему координат, в которой положение точки определяется углом 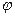между радиус‑вектором точки и осью 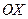и расстоянием 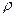от точки до начала координат. Поскольку точки, равностоящие от центра, все либо одновременно принадлежат меньшему кругу, либо нет, то вероятность попадания в этот круг равна отношению радиусов: .

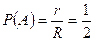Итак, мы получили в одной и той же задаче два разных ответа. Причина заключается в том, что понятие геометрической вероятности не инвариантно относительно преобразований рассматриваемой области 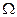и зависит от того, как задана мера .

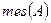Отметим, что для нас предпочтительнее первый способ решения. l