Решение. Шарик в канале совершает сложное движение, поэтому необходимо рассматривать его движение как сумму относительного и переносного движений

Шарик в канале совершает сложное движение, поэтому необходимо рассматривать его движение как сумму относительного и переносного движений. Введём подвижную (ПСО) и неподвижную (ИСО) системы отсчёта (рис. 3.8).
ИСО выбираем так, чтобы ось O1Z1 являлась осью вращения тела А. ПСО закрепляем на теле А таким образом, чтобы ось ОХ совпадала с траекторией относительного движения точки. ПСО вместе с телом А совершает вращательное движение с переносной угловой скоростью 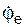 =
=  , вектор
, вектор 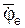 которой расположен на оси O1Z1 и направлен вверх.
которой расположен на оси O1Z1 и направлен вверх.
Изобразим точку М на траектории относительного движения в произвольный момент времени (Х = f(t) > 0). При этом текущие значения относительной скорости Vr и относительного ускорения ar направлены в сторону возрастания координаты Х. Изобразим на рис. 3.8 начальную координату Х0 и начальную относительную скорость Vr0. Так как по условию задания 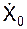 > 0, то вектор Vr0 направлен в сторону возрастания координаты Х.
> 0, то вектор Vr0 направлен в сторону возрастания координаты Х.
Траекторией переносного движения является окружность с центром О на оси O1Z1 вращения и радиусом r = OM = Х = f(t). Переносная скорость Vе направлена так, как это показано на рис. 3.8 – параллельна координатной оси OY подвижной системы отсчёта.
Поскольку переносное вращение является равномерным (I 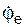 I = ωe = const, где ωе – модуль переносной угловой скорости
I = ωe = const, где ωе – модуль переносной угловой скорости 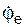 ), то переносное ускорение
), то переносное ускорение
ae = 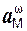 ,
,
где 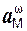 – центростремительное ускорение точки М тела А.
– центростремительное ускорение точки М тела А.
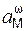 = (ωе)2·ОМ = (ωе)2·Х.
= (ωе)2·ОМ = (ωе)2·Х.
Согласно правилу векторного произведения (или правилу Жуковского) ускорение Кориолиса (ac = 2 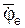 ×Vr) направлено так же, как и вектор Vе переносной скорости. Модуль ускорения ac Кориолиса равен
×Vr) направлено так же, как и вектор Vе переносной скорости. Модуль ускорения ac Кориолиса равен
ac = 2·ωe·Vr·sin( 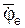 ,Vr) = 2·ωe·Vr·sin(900) = 2·ωe·Vr·1 = 2·ωe·Vr.
,Vr) = 2·ωe·Vr·sin(900) = 2·ωe·Vr·1 = 2·ωe·Vr.
Деформация Δ пружины в произвольный момент времени определяется формулой
Δ = Х – l0.
На рис. 3.8 приведены только кинематические характеристики точки М при её относительном движении.
Запишем основное уравнение динамики относительного движения.
m·ar = ΣFiЕ + ΣRiЕ + Фе + Фс.
Определим силы, действующие на материальную точку, и покажем их на рис. 3.9.

Кориолисова сила инерции Фс направлена противоположно кориолисову ускорению aс, а её модуль равен
Φс = m·ac = m·(2·ωe·Vr).
Переносная сила инерции Фе направлена противоположно переносному ускорению aе, а её модуль равен
Φе = m·ae = m·(ωe)2·Х.
К реакциям внешних связей RiЕ относятся силы: Fyn – сила упругости пружины; N1, N2 – реакции гладкой поверхности канала, по которому перемещается точка М.
Fyn = c·Δ = c·(Х – l0).
Реакция N1 направлена вертикально вверх (навстречу вектору G силы тяжести точки). Реакция N2 расположена в горизонтальной плоскости OXY и направлена противоположно вектору Фс кориолисовой силы инерции.
С учётом изложенного основное уравнение динамики относительного движения принимает вид
m·ar = G + Fyn + N1 + N2 + Фе + Фс.
Запишем дифференциальные уравнения относительного движения материальной точки. Для этого последнее векторное выражение спроецируем на координатные оси ПСО:
m· 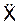 = – Fyn + Φe = – c·Δ + m·(ωe)2·Х = – c·(Х – l0) + m·(ωe)2·Х =
= – Fyn + Φe = – c·Δ + m·(ωe)2·Х = – c·(Х – l0) + m·(ωe)2·Х =
= – c·x + c·l0 + m·(ωe)2·Х; (1)
m·  = N2 – Φc = N2 – m·(2·ωe·
= N2 – Φc = N2 – m·(2·ωe· 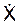 ); (2)
); (2)
m· 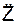 = – G + N1. (3)
= – G + N1. (3)
Поскольку относительное ускорение ar на координатные оси OY, OZ не проецируется (  = 0;
= 0; 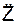 = 0), то с учётом исходных данных курсового задания уравнения (2), (3) принимают вид:
= 0), то с учётом исходных данных курсового задания уравнения (2), (3) принимают вид:
N2 = m·(2·ωe· 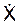 ); (2I)
); (2I)
N1 = m·g. (3I)
Дифференциальное уравнение (1) приведем к виду
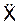 + (c/m – (ωe)2)·X = c·l0/m. (1I)
+ (c/m – (ωe)2)·X = c·l0/m. (1I)
Поскольку c/m – (ωe)2 = k2 и c·l0/m = b = const, то уравнение (1I) принимает вид
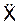 + k2·X = b. (1II)
+ k2·X = b. (1II)
Согласно положениям высшей математики общее решение дифференциального уравнения (1II) будем искать по формуле
X = X* + X**,
где X* – общее решение дифференциального уравнения вида 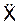 + k2·X = 0; X** – частное решение дифференциального уравнения (1II).
+ k2·X = 0; X** – частное решение дифференциального уравнения (1II).
Приступаем к определению общего решения X* дифференциального уравнения вида 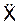 + k2·X = 0. Это решение зависит от знака величины c/m – (ωe)2 = k2. Если k2 > 0, то X* = A·sin(k·t + β). Если k2 < 0, то X* = C1·ek·t + C2·e-k·t. Определим значения k2 и k:
+ k2·X = 0. Это решение зависит от знака величины c/m – (ωe)2 = k2. Если k2 > 0, то X* = A·sin(k·t + β). Если k2 < 0, то X* = C1·ek·t + C2·e-k·t. Определим значения k2 и k:
k2 = c/m – (ωe)2 = 20/0,09 – (3,14)2 = 22,540 c-2 > 0; k = 4,747 c-1.
Поскольку k2 > 0, то X* = A·sin(4,747·t + β).
Частное решение X** дифференциального уравнения (1II) зависит от вида его правой части. Поскольку его правая часть постоянна (b = c·l0/m = const), то его частное решение будем искать в виде X**= B = const.
При частном решении уравнение (1II) принимает вид
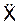 ** + k2 ·X** = b.
** + k2 ·X** = b.
Так как 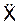 ** = (
** = ( 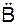 ) = 0, то имеем k2·B = c·l0/m. Отсюда получим
) = 0, то имеем k2·B = c·l0/m. Отсюда получим
B = (c·l0/m)/k2 = (20·0,1/0,09)/22,54 = 0,985 м.
Итак, общее решение дифференциального уравнения (1) имеет вид
X = X* + X** = A·sin(4,747·t + β) + 0,985,
где А и β – постоянные интегрирования, зависящие от начальных условий относительного движения.
В нашем случае: X0 = 0,2 м; 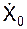 = 0,3 м/с. Для определения постоянных интегрирования А и β определим проекцию относительной скорости Vr на ось ОХ.
= 0,3 м/с. Для определения постоянных интегрирования А и β определим проекцию относительной скорости Vr на ось ОХ.
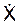 = dX/dt = A·cos(4,747·t + β)·4,747.
= dX/dt = A·cos(4,747·t + β)·4,747.
При t0 = 0 имеем:
X0 = 0,2 = A·sin(β) + 0,985;
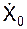 = 0,3 = A·cos(β)·4,747.
= 0,3 = A·cos(β)·4,747.
Преобразуем эту систему уравнений к виду:
0,2 – 0,985 = A·sin(β) = – 0,785;
0,3/4,747 = A·cos(β) = 0,063.
Возведя в квадратную степень левые и правые части уравнений и сложив их, получим:
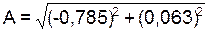 = 0,787 м;
= 0,787 м;
sin(β) = – 0,785/A = – 0,785/0,787 = – 0,997;
cos(β) = 0,063/0,787 = 0,080.
Поскольку sin(β) < 0, а cos(β) > 0, то величину угла β определим по формуле β = 2π – α, где α = arcsin(0,987) = 1,482 рад или α = arcсоs(0,080) = 1,482 рад. Тогда
β = 2·π – α = 2·3,14 – 1,482 = 4,798 рад.
В окончательном виде имеем:
X = 0,787·sin(4,747·t + 4,798);
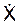 = 3,776·cos(4,747·t + 4,798).
= 3,776·cos(4,747·t + 4,798).
По условиям задания кроме значения координаты X(t1) необходимо определить модуль N(t1) нормальной реакции Nв момент времени t1.
N(t1) = 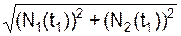 .
.
С учетом выражений (2I), (3I) имеем
N(t1) = 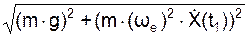 .
.
Результаты расчётов помещают в таблицу.
| Уравнение относительного движения точки | Вычисляемые величины | ||
| X(t1), м | 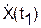 , м/с , м/с
| N(t1), H | |
| X = 0,787·sin(4,747·t + 4,798) | 0,666 | 2,006 | 1,986 |
По результатам решения желательно построить графики зависимостей X = f1(t), N = f2(t).
Вопросы и задания для самоконтроля
1. Записать основное уравнение динамики относительного движения.
2. Записать формулу для определения переносной силы инерции.
3. Записать формулу для определения кориолисовой силы инерции.
4. Записать основное уравнение динамики относительного движения точки для случая, когда переносное движение есть неравномерное вращение относительно неподвижной оси, а относительное движение прямолинейное.
5. Записать основное уравнение динамики относительного движения точки для случая, когда переносное движение есть равномерное вращение относительно неподвижной оси, а относительное движение прямолинейное.
6. Записать основное уравнение динамики относительного движения точки для случая, когда переносное движение есть поступательное неравномерное криволинейное движение, а относительное движение прямолинейное.
7. Записать основное уравнение динамики относительного движения точки для случая, когда переносное движение есть прямолинейное и равномерное движение, а относительное движение прямолинейное.
8. Сформулировать принцип относительности классической механики.
Дата добавления: 2015-05-30; просмотров: 1414;
