Характеристик центра масс механической системы
Решение задач, в которых требуется определить уравнение траектории движения центра масс, его скорость и ускорение, проводят по алгоритму, представляющему собой заданную последовательность действий исполнителя.
1. Выбрать систему отсчёта.
2. Определить массу механической системы по формуле m = ΣmCi.
3. Записать координаты центров тяжестей каждого из тел механической системы, выразив их в функции времени: XCi = XCi(t); YCi = YCi(t); ZCi = Zci(t).
4. Определить координаты центра масс механической системы по формулам: XC = ΣmCi·XCi/m; YC = ΣmCi·YCi/m; ZC = ΣmCi·ZCi/m. Полученные координаты XC, Yc, ZC окажутся функциями времени, т. е. эти координаты окажутся параметрическими уравнениями движения центра масс.
5. Для нахождения явных уравнений траектории движения центра масс системы материальных точек надо из последних уравнений исключить время t.
6. Определить проекции 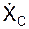 ,
,  ,
, 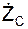 скорости центра масс и модуль этой скорости по формулам:
скорости центра масс и модуль этой скорости по формулам: 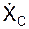 = ΣmCi·
= ΣmCi· 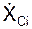 /m;
/m;  = ΣmCi·
= ΣmCi· 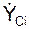 /m;
/m; 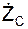 = ΣmCi·
= ΣmCi· 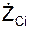 /m; VC =
/m; VC = 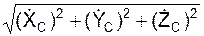 ;
;
7. .Для ориентации вектора скорости VC центра масс в пространстве определить направляющие косинусы по формулам: cos(VC, i) = 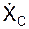 / VC; cos(VC, k) =
/ VC; cos(VC, k) = 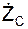 / VC; cos(VC, k) =
/ VC; cos(VC, k) = 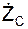 / VC.
/ VC.
8. Определить проекции 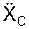 ,
, 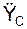 ,
, 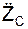 ускорения центра масс и модуль этого ускорения по формулам:
ускорения центра масс и модуль этого ускорения по формулам: 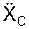 = ΣmCi·
= ΣmCi· 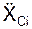 /m;
/m; 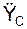 = ΣmCi·
= ΣmCi· 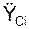 /m;
/m; 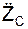 = ΣmCi·
= ΣmCi· 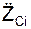 /m; aC =
/m; aC = 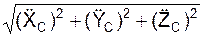 .
.
9. Определить направляющие косинусы по формулам: cos(aC, i)= 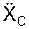 /aC; cos(aC, j)=
/aC; cos(aC, j)= 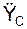 /aC; cos(aC, k)=
/aC; cos(aC, k)= 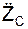 /aC.
/aC.
10. Для момента времени t1 определить кинематические характеристики центра масс. Результаты вычислений свести в таблицу и при необходимости проиллюстрировать рисунком.
Дата добавления: 2015-05-30; просмотров: 1174;
