Осевые моменты инерции однородных пластинок
| Форма тела | JOX | JOY | JOZ | Форма тела |
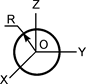
| m·R2/2 | m·R2/4 | m·R2/4 |
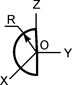
|
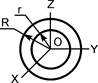
| m·(R2+r2)/2 | m·(R2+r2)/4 | m·(R2+r2)/4 |
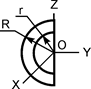
|
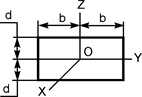
| m·(b2+d2)/3 | m·d2/3 | m·b2/3 |
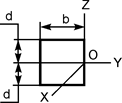
|
Окончание табл. 4.1
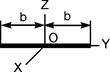
| m·b2/3 | m·b2/3 |
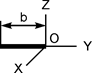
| |
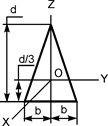
| m·(3b2+d2)/18 | m·d2/18 | m·b2/6 |
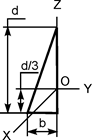
|
При выполнении курсовых заданий довольно часто требуется определить момент инерции относительно оси, которая через центр масс тела не проходит. Для этой цели используют теорему Штейнера о зависимости между моментом инерции твёрдого тела относительно параллельных осей.
Момент инерции твёрдого тела относительно оси равен сумме его момента относительно параллельной оси, проходящей через центр масс С, и произведения массы твёрдого тела на квадрат расстояния между параллельными осями.
Согласно этой теореме определим момент инерции круглой однородной пластины относительно оси ОХ (рис. 4.3).
JOX = JCX +m·(ОС)2 = JCX + m·d2 = m·R2/2 + m·d2.
Для твёрдого тела в случае неоднородного распределения масс в его поперечном сечении, перпендикулярном оси вращения, момент инерции вычисляют по формуле
JOX = m·(iOX)2,
где iOX – радиус инерции тела относительно оси вращения ОХ, м.
Радиус инерции твёрдого тела относительно оси вращения – величина, произведение квадрата которой на массу тела равно моменту инерции тела относительно этой оси.
 |
Таким образом, если поперечное сечение твёрдого тела по отношению к оси его вращения имеет сложную конфигурацию, то массу тела располагают равномерно на окружности, радиус которой равен радиусу инерции i.
Радиус инерции определяют экспериментальным путём по специальной методике.
Если надо вычислить момент инерции механической системы, состоящей из нескольких твёрдых тел, причем момент инерции каждого из порознь взятых твёрдых тел известен, то момент инерции системы определяют как сумму моментов инерции всех твёрдых тел, входящих в систему, относительно той же оси.
JОХ = ΣJiОХ,
где JiОХ – момент инерции i-го тела механической системы относительно оси вращения ОХ.
Для механических систем в теоретической механике используют понятие «радиус инерции механической системы относительно оси вращения».
Радиус инерции механической системы относительно оси вращения – величина, квадрат которой равен отношению момента инерции механической системы относительно данной оси к массе этой системы.
iОХ = 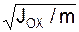 .
.
Вопросы и задания для самоконтроля
1. Сформулировать определение понятия «механическая система».
2. Сформулировать определение понятия «свободная механическая система».
3. Сформулировать определение понятия «несвободная механическая система».
4. Сформулировать определение понятия «внешние силы».
5. Сформулировать определение понятия «внутренние силы».
6. Сформулировать определение понятия «неизменяемая механическая система».
7. Сформулировать определение понятия «центр масс механической системы».
8. Записать формулу для определения радиус-вектора центра масс механической системы.
9. Записать формулу для определения главного вектора активных сил.
10. Записать формулу для определения главного вектора реакций внешних связей.
11. Записать формулу для определения главного вектора реакций внутренних связей.
12. Записать формулу для определения вектора скорости центра масс механической системы.
13. Записать формулу для определения вектора ускорения центра масс механической системы.
14. Записать формулы для определения проекций вектора скорости центра масс механической системы на координатные оси.
15. Записать формулы для определения проекций вектора ускорения центра масс механической системы на координатные оси.
16. Записать формулу для определения модуля скорости центра масс механической системы.
17. Записать формулу для определения модуля ускорения центра масс механической системы.
18. Что является мерой инертности при поступательном движении твёрдого тела?
19. Что является мерой инертности при вращательном движении твёрдого тела?
20. Сформулировать определение понятия «момент инерции тела относительно оси вращения».
21. Что характеризует момент инерции тела относительно оси вращения?
22. Сформулировать теорему Штейнера.
23. Записать формулу для определения момента инерции тела относительно вертикальной оси вращения.
24. Сформулировать определение «радиус инерции твёрдого тела относительно оси вращения».
25. Записать формулу для определения момента инерции механической системы.
Дата добавления: 2015-05-30; просмотров: 3435;
