Следствия из теоремы о движении центра масс

1. Если геометрическая сумма активных сил и реакций внешних связей постоянно равна нулю (Σ + Σ = 0), то центр масс механической системы находится в покое или движется равномерно и прямолинейно.

Таким образом, если Σ + Σ = 0, то a_С = 0, т. е. V_С = const. Если начальная скорость V_С0 центра масс равна нулю, то центр масс находится в покое. Если же V_С0 ≠ 0, то центр масс движется прямолинейно и равномерно с этой скоростью.

2. Если суммы проекций активных сил и реакций внешних связей на какую-либо ось остаются всё время равными нулю, то проекция центра масс механической системы на эту ось неподвижна или движется равномерно.

Действительно, если Σ + Σ = 0, то 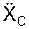= 0, т. е. 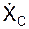= const. Если при этом в начальный момент времени 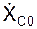= 0, то 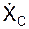= 0, Х_С = const, т. е. координата Х_С центра масс остается постоянной.

Следствия из теоремы о движении центра масс выражают закон сохранения движения центра масс механической системы.

С помощью теоремы о движении центра масс механической системы решают задачи, в которых рассматривается только поступательная часть движения тел, образующих механическую систему.

Рекомендуется следующий алгоритм решения задач.

1. Выбирается система отсчёта.

2. К механической системе прикладываются все активные силы и реакции внешних связей.

3. Записывается теорема о движении центра масс (m·a_c = Σ + Σ = F^E + R^E) в проекциях на оси системы отсчёта:

m· 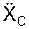= Σ + Σ ;

m· = Σ + Σ ;

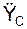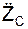m· = Σ + Σ .

4. Вычисляются суммы проекций активных сил и реакций внешних связей на оси системы отсчёта и подставляются в последние выражения.

5. В зависимости от условий решается прямая либо обратная задача динамики.

Поскольку для заочной формы обучения курсовых заданий на использование теоремы о движении центра масс механической системы не предусмотрено, то примеры решения таких задач в данном учебно-методическом пособии не приведены.

Вопросы и задания для самоконтроля

1. Сформулировать теорему о движении центра масс механической системы.

2. Записать векторную формулу, выражающую теорему о движении центра масс механической системы.

3. Записать дифференциальные уравнения движения центра масс механической системы в декартовой системе отсчёта.

4. Сформулировать первое следствие из теоремы о движении центра масс механической системы.

5. Сформулировать второе следствие из теоремы о движении центра масс механической системы.