Механической системы

5.2.1. Теорема об изменении количества движения

материальной точки

В этой теореме используются понятия «количество движения» и «импульс силы». Введём эти понятия.

Количество движения материальной точки – векторная мера механического движения, равная произведению массы точки на её скорость.

Согласно определению вектор количества движения m·V имеет такое же направление, как и вектор скорости V точки. Количество движения m·V является векторной мерой механического движения. Количество движения имеет размерность [кг·м/с].

В теоретической механике используют понятие «элементарный импульс силы».

Элементарный импульс силы – векторная мера действия силы, равная произведению силы на элементарный промежуток времени её действия.

S_i = P_i ·Δt,

где S_i – элементарный импульс силы; P_i – сила; Δt – элементарный промежуток времени.

Равнодействующая системы сил, действующих на точку, определяется по формуле P = ΣP_i.

Если постоянная по модулю и направлению сила P_i действует на точку в течение промежутка времени Δt = t₂ – t₁, то элементарнымимпульсом силы за конечный промежуток времени является вектор

S_i = P_i·Δt = P_i·(t₂ – t₁).

Направление этого вектора совпадает с направлением силы, а его модуль равен произведению модуля силы на время её действия:

S_i = P_i·(t₂ – t₁).

В общем случае импульс S_i силы P_i за промежуток времени Δt = (t₂ – t₁) определяется векторным интегралом от вектора P_i по скалярному аргументу t:

S_i = .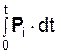

Импульс силы за конечный промежуток времени – величина, равная определённому интегралу от элементарного импульса силы, где пределами интеграла являются моменты начала и конца данного промежутка времени.

Импульс равнодействующей Р нескольких сил P_i за некоторый промежуток времени равен геометрической сумме импульсов соответствующих сил за этот же промежуток времени.

S = ΣS_i.

В проекциях на координатные оси имеем:

S_ОХ = ΣS_iОХ; S_OY = ΣS_iOY; S_OZ = ΣS_iOZ.

Проекция импульса равнодействующей на ось системы отсчета равна алгебраической сумме проекций импульсов составляющих сил на ту же ось.

Теорема об изменении количества движения материальной точки в дифференциальной форме выражается формулой

d(m·V)/dt = P.

Производная по времени от количества движения материальной точки геометрически равна равнодействующей сил, приложенных к этой точке.

Теорема об изменении количества движения материальной точки в интегральной (конечной) форме приобретает вид

m·V₂ – m·V₁ = ΣS_i,

где V₂, V₁ – скорости точки соответственно в конечный и начальный моменты времени.

Изменение количества движения материальной точки за некоторый промежуток времени равно геометрической сумме импульсов сил, приложенных к точке за тот же промежуток времени.

Эту теорему называют также теоремой импульсов.

Последнему векторному равенству соответствуют три уравнения в проекциях на оси системы отсчёта OXYZ:

m·V_2ОХ – m·V_1ОХ = ΣS_iОХ;

m·V_2OY – m·V_1OY = ΣS_iOY;

m·V_2OZ – m·V_1OZ = ΣS_iOZ,

где V_2ОХ, V_2OY, V_2OZ, V_1ОХ, V_1OY, V_1OZ – проекции конечной и начальной скоростей точки на координатные оси системы отсчёта

Изменение проекции количества движения материальной точки на координатную ось за некоторый промежуток времени равно сумме проекций на ту же ось импульсов, приложенных к точке сил за тот же промежуток времени.

Большинство практических задач решается по уравнениям в проекциях на оси координат.

5.2.2. Теорема об изменении количества движения

механической системы

Рассмотрим движение неизменяемой механической системы под действием активных сил , реакций внешних связей и внутренних сил в инерциальной системе отсчёта OXYZ (рис. 5.4).

Количество движения механической системы – величина, равная сумме количеств движения всех материальных точек, образующих механическую систему.

Количество движения K механической системы определяют по формуле

K = Σm_Ci·V_Ci = m·V_C.

Это выражение показывает, что вектор количества движения механической системы равен произведению массы системы на скорость её центра масс.

Проецируя последнее векторное равенство на координатные оси, получим:

K_OX = m·V_COX; K_OY = m·V_COY; K_OZ = m·V_COZ,

где V_COX, V_COY, V_COZ – проекции скорости центра масс механической системы на координатные оси.

Проекция количества движения механической системы на каждую координатную ось равна произведению массы системы на проекцию скорости центра масс на эту же ось.

Теорема об изменении количества движения механической системы выражается векторным равенством

dK/dt = Σ + Σ .

Производная по времени от количества движения механической системы равна геометрической сумме активных сил и реакций внешних связей.

Последнему векторному равенству соответствует три уравнения в проекциях на координатные оси:

dK_OX/dt = Σ + Σ ;

dK_OY/dt = Σ + Σ ;

dK_OZ/dt = Σ + Σ ,

где dK_OX/dt, dK_OY/dt, dK_OZ/dt – производные по времени от проекций количества движения механической системы на соответствующие координатные оси системы отсчёта.

Производная по времени от проекции количества движения механической системы на координатную ось равна сумме проекций активных сил и реакций внешних связей на ту же ось.

Необходимо отметить, что изменение количества движения механической системы вызывается только внешними силами, к которым относятся активные силы и реакции внешних связей.