Следствия из теоремы. 1. Если линия действия равнодействующей (Р= Σ +Σ + Σ ) приложенных к материальной точке сил всё время проходит через некоторый неподвижный

1. Если линия действия равнодействующей (Р= Σ +Σ + Σ ) приложенных к материальной точке сил всё время проходит через некоторый неподвижный центр, то момент количества движения материальной точки относительно этого центра остается постоянным.

Действительно, если ΣM_О( ) + ΣM_О( ) + ΣM_О( ) = 0, то dL_О/dt = 0 и, следовательно, L_О = const.

Центральная сила – сила, линия действия которой постоянно проходит через некоторую точку, неподвижную в данной системе отсчёта и называемую центром силы.

Покажем, что линия действия равнодействующей силы Р постоянно проходит через центр О. Тогда главный момент М_О активных сил , реакций внешних связей и внутренних сил равен нулю:

М_О = ΣM_О( ) + ΣM_О( ) + ΣM_О( ) = 0.

Отсюда следует, что L_О = const.

Из следствия 1 вытекает, что плоскость, в которой находятся вектор m·V количества движения точки и центр О, не изменяет своего положения, т. е. траектория лежит в одной плоскости.

2. Если момент равнодействующей приложенных к материальной точке активных сил, реакций внешних связей и внутренних сил относительно некоторой оси всё время равняется нулю, то момент количества движения материальной точки относительно этой оси остается постоянным.

Если, например, M_OX(P) = ΣM_OX( ) + ΣM_OX( ) + ΣM_OX( ) = 0, то dL_OX/dt = 0 и, следовательно, L_OX = const.

5.3.3. Кинетический момент механической

системы относительно центра и оси

Кинетический момент или главный момент количеств движения механической системы относительно данного центра – величина, равная сумме моментов количеств движения всех точек механической системы относительно этого центра.

Момент количества движения каждой материальной точки C_i системы (рис. 5.9) относительно центра О определяется по формуле

L_CiO = r_Ci×(m_Ci·V_Ci).

Кинетический момент механической системы относительно центра О равен геометрической сумме моментов количеств движения материальных точек системы:

Кинетический момент или главный момент количеств движения механической системы относительно оси – величина, равная сумме моментов количеств движения всех точек механической системы относительно этой оси.

Определим кинетический момент механической системы относительно оси OZ (рис. 5.10).

Момент количества движения L_CiOZ каждой точки C_i системы относительно оси вращения OZ определяется по формуле

L_CiOZ = (m_Ci· 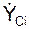)·X_Ci – (m_Ci· 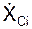)·Y_Ci.

Кинетический момент механической системы относительно оси OZ вращения равен

L_OZ = ΣL_CiOZ.

Аналогичным образом определяются кинетические моменты механической системы относительно осей вращения OX, OY:

L_CiOX = (m_Ci· 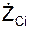)·Y_Ci – (m_Ci· 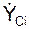)·Z_Ci;

L_OX = ΣL_CiOX;

L_CiOY = (m_Ci· 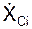)·Z_Ci – (m_Ci· 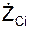)·X_Ci;

L_OY = ΣL_CiOY.

5.3.4. Теорема об изменении кинетического

момента механической системы

Рассмотрим движение неизменяемой механической системы под действием активных сил , реакций внешних связей и внутренних сил (рис. 5.11).

Выберем некоторый неподвижный центр О и определим изменение момента количества движения i-й точки относительно этого центра:

dL_CiО/dt = M_O( ) + M_O( ) + M_O( ),

где i изменяется от 1 до n.

Просуммируем полученные n уравнений:

ΣdL_CiO/dt = dL_O/dt = ΣM_O( ) + ΣM_O( ) + ΣM_O( ),

где L_O – вектор кинетического момента механической системы относительно центра О.

Как известно, для неизменяемой механической системы геометрическая сумма внутренних сил равна нулю (Σ = 0). Отсюда следует, что и геометрическая сумма моментов этих сил относительно любого центра равна нулю. Приняв за такой центр точку О, имеем ΣM_O( ) = 0. Тогда получим

dL_O/dt = ΣM_O( ) + ΣM_O( ).

Это равенство выражает теорему об изменении кинетического момента механической системы.

Производная по времени от кинетического момента механической системы относительно некоторого неподвижного центра равна геометрической сумме моментов приложенных к системе активных сил и реакций внешних связей относительно того же центра.

Последнему векторному равенству соответствуют три равенства в проекциях на оси координат:

dL_OX/dt = ΣM_OX( ) + ΣM_OX( );

dL_OY/dt = ΣM_OY( ) + ΣM_OY( );

dL_OZ/dt = ΣM_OZ( ) + ΣM_OZ( ),

где L_OX, L_OY, L_OZ – кинетические моменты механической системы относительно координатных осей; ΣM_OX( ), ΣM_OY( ), ΣM_OZ( ) – суммы моментов активных сил относительно координатных осей; ΣM_OX( ), ΣM_OY( ), ΣM_OZ( ) – суммы моментов реакций внешних связей относительно координатных осей.

Производная по времени от кинетического момента механической системы относительно некоторой оси равна сумме моментов приложенных к системе активных сил и реакций внешних связей относительно той же оси.