Следствия из теоремы
1. Если геометрическая сумма моментов, приложенных к системе активных сил и реакций внешних связей относительно некоторого неподвижного центра, остается всё время равной нулю, то кинетический момент механической системы относительно этого центра остается постоянным.
Если ΣMО(  ) + ΣMО(
) + ΣMО(  ) = 0, то dLО/dt = 0 и, следовательно, LО = const.
) = 0, то dLО/dt = 0 и, следовательно, LО = const.
2. Если алгебраическая сумма моментов, приложенных к механической системе активных сил и реакций внешних связей относительно некоторой оси, остается всё время равной нулю, то кинетический момент механической системы относительно этой же оси остается постоянным.
Действительно, например, если ΣMOX(  ) + ΣMOX(
) + ΣMOX(  ) = 0, то dLOX/dt = 0 и, отсюда следует, что LOX = const.
) = 0, то dLOX/dt = 0 и, отсюда следует, что LOX = const.
Следствия из теоремы об изменении кинетического момента механической системы выражают закон сохранения кинетического момента механической системы.
5.3.5. Варианты курсового задания Д 3
«Применение теоремы об изменении
кинетического момента к определению угловой
скорости твёрдого тела»
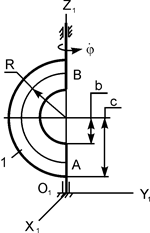
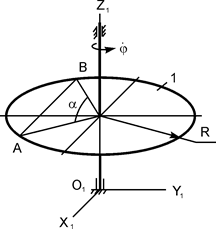
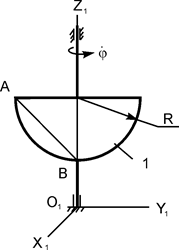
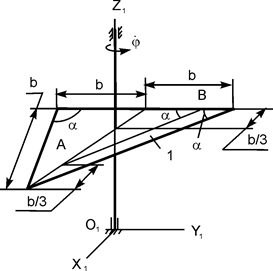
В исходном положении тело Н (тело 1) массой m1 вращается вокруг вертикальной оси O1Z1 с постоянной угловой скоростью 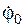 ; при этом в точке О жёлоба АВ тела 1 на расстоянии АО от точки А, отсчитываемом вдоль жёлоба, находится материальная точка К массой m2. В некоторый момент времени (t0 = 0) на систему начинает действовать пара сил с алгебраическим моментом MOZ = MOZ(t). В момент времени t = τ действие пары сил прекращается.
; при этом в точке О жёлоба АВ тела 1 на расстоянии АО от точки А, отсчитываемом вдоль жёлоба, находится материальная точка К массой m2. В некоторый момент времени (t0 = 0) на систему начинает действовать пара сил с алгебраическим моментом MOZ = MOZ(t). В момент времени t = τ действие пары сил прекращается.
Определить значение угловой скорости тела 1 в момент времени t = τ (  (τ) = ?).
(τ) = ?).
Тело 1 вращается по инерции с угловой скоростью 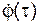 .
.
В некоторый момент времени t1 = 0 (t1 – новое начало отсчёта времени) точка К (самоходный механизм) начинает относительное движение из точки О вдоль жёлоба АВ (в направлении от точки А к точке В) по закону ОК = S = S(t1).
Определить значение угловой скорости тела 1 в момент времени t1 = T (  (Т) = ?).
(Т) = ?).
Тело 1 рассматривать как однородную пластинку. Расчётные схемы механизмов и необходимые для решения данные приведены в табл. 5.1.
Таблица 5.1
| Номер варианта | Расчётная схема механизма | Исходные данные |
|
m1 = 32 кг;
m2 = 10 кг;
 = – 1 рад/с;
b = 1, м;
с = 1, 5 м;
R = 1, 2 м;
АО = π·R/6 м;
MOZ = – 29,6·t2 Н·м;
τ = 3 с;
ОК = (5·π·R/12)·t1 м;
Т = 1 с = – 1 рад/с;
b = 1, м;
с = 1, 5 м;
R = 1, 2 м;
АО = π·R/6 м;
MOZ = – 29,6·t2 Н·м;
τ = 3 с;
ОК = (5·π·R/12)·t1 м;
Т = 1 с
| |
|
m1 = 200 кг;
m2 = 60 кг;
 = – 2 рад/с;
R = 2 м;
α = 120о;
АО = 0,866 м;
MOZ = 101 Н·м;
τ = 5 с;
ОК = 1,732·(t1)2 м;
Т = 1 с = – 2 рад/с;
R = 2 м;
α = 120о;
АО = 0,866 м;
MOZ = 101 Н·м;
τ = 5 с;
ОК = 1,732·(t1)2 м;
Т = 1 с
| |
|
m1 = 120 кг;
m2 = 40 кг;
 = 0 рад/с;
b = 2 м;
АО = 0 м;
MOZ = 120·t Н·м;
τ = 4 с;
ОК=(1,414/4)·(t1)2 м;
Т = 2 с = 0 рад/с;
b = 2 м;
АО = 0 м;
MOZ = 120·t Н·м;
τ = 4 с;
ОК=(1,414/4)·(t1)2 м;
Т = 2 с
|
Продолжение табл. 5.1

|
m1 = 16 кг;
m2 = 5 кг;
 = – 3 рад/с;
R = 1 м;
α = 30о;
АО = 0,4 м;
MOZ = 21·t Н·м;
τ = 2 с;
ОК=0,6·t1 м;
Т = 2 с = – 3 рад/с;
R = 1 м;
α = 30о;
АО = 0,4 м;
MOZ = 21·t Н·м;
τ = 2 с;
ОК=0,6·t1 м;
Т = 2 с
| |
|
m1 = 66 кг;
m2 = 10 кг;
 = 1,5 рад/с;
b = 2 м;
c = 1,5 м;
АО = 0 м;
MOZ = 15· = 1,5 рад/с;
b = 2 м;
c = 1,5 м;
АО = 0 м;
MOZ = 15·  Н·м;
τ = 4 с;
ОК=0,5·t1 м;
Т = 2,5 с Н·м;
τ = 4 с;
ОК=0,5·t1 м;
Т = 2,5 с
| |
|
m1 = 160 кг;
m2 = 80 кг;
 = – 1,25 рад/с;
b = 1,5 м;
R = 2,5 м;
α = 30о;
АО = π·b/6 м;
MOZ = – 700·t Н·м;
τ = 3 с;
ОК=(6·π·b/18)·(t1)2 м;
Т = 1 с = – 1,25 рад/с;
b = 1,5 м;
R = 2,5 м;
α = 30о;
АО = π·b/6 м;
MOZ = – 700·t Н·м;
τ = 3 с;
ОК=(6·π·b/18)·(t1)2 м;
Т = 1 с
|
Продолжение табл. 5.1
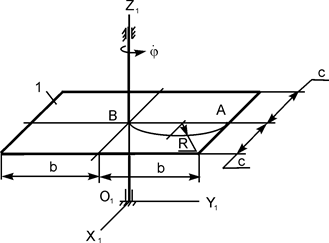
|
m1 = 300 кг;
m2 = 50 кг;
 = – 2 рад/с;
b = 1,6 м;
c = 1 м;
R = 0,8 м;
АО = 0 м;
MOZ = 968 Н·м;
τ = 1 с;
ОК=(π·R/2)·(t1)2 м;
Т = 1 с = – 2 рад/с;
b = 1,6 м;
c = 1 м;
R = 0,8 м;
АО = 0 м;
MOZ = 968 Н·м;
τ = 1 с;
ОК=(π·R/2)·(t1)2 м;
Т = 1 с
| |
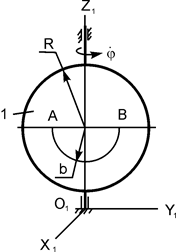
|
m1 = 80 кг;
m2 = 20 кг;
 = 0 рад/с;
b = 1,2 м;
R = 2 м;
АО = π·b/2 м;
MOZ = 240· = 0 рад/с;
b = 1,2 м;
R = 2 м;
АО = π·b/2 м;
MOZ = 240·  Н·м;
τ = 4 с;
ОК = (π·b/4)·t1 м;
Т = 2 с Н·м;
τ = 4 с;
ОК = (π·b/4)·t1 м;
Т = 2 с
| |
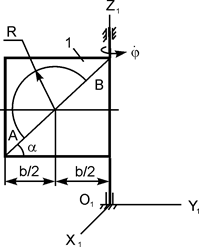
|
m1 = 20 кг;
m2 = 5 кг;
 = 5 рад/с;
b = 1,2 м;
R = 0,4 м;
α = 45о;
АО = π·R/4 м;
MOZ = – 29,2·t Н·м;
τ = 3 с;
ОК=(3·π·R/4)·(t1)2 м;
Т = 1 с = 5 рад/с;
b = 1,2 м;
R = 0,4 м;
α = 45о;
АО = π·R/4 м;
MOZ = – 29,2·t Н·м;
τ = 3 с;
ОК=(3·π·R/4)·(t1)2 м;
Т = 1 с
|
Продолжение табл. 5.1
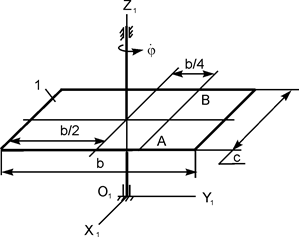
|
m1 = 100 кг;
m2 = 40 кг;
 = 2 рад/с;
b = 2 м;
с = 1,414 м;
АО =0,707 м;
MOZ = – 90· = 2 рад/с;
b = 2 м;
с = 1,414 м;
АО =0,707 м;
MOZ = – 90· 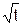 Н·м;
τ = 4 с;
ОК=(0,707/2)·(t1)2 м;
Т = 1 с Н·м;
τ = 4 с;
ОК=(0,707/2)·(t1)2 м;
Т = 1 с
| |
|
m1 = 60 кг;
m2 = 20 кг;
 = – 1 рад/с;
b = 2 м;
R = 2 м;
АО = 0 м;
MOZ = 40·t Н·м;
τ = 2 с;
ОК = 0,4·(t1)2 м;
Т = 2 с = – 1 рад/с;
b = 2 м;
R = 2 м;
АО = 0 м;
MOZ = 40·t Н·м;
τ = 2 с;
ОК = 0,4·(t1)2 м;
Т = 2 с
| |
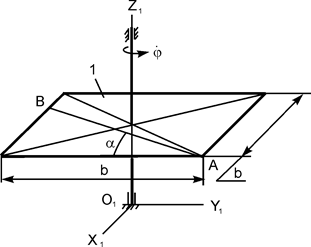
|
m1 = 40 кг;
m2 = 10 кг;
 = – 3 рад/с;
b = 1 м;
R = 2 м;
АО = 0 м;
MOZ = 50·t2 Н·м;
τ = 3 с;
ОК = (π·b/3)·(t1)2 м;
Т = 2 с = – 3 рад/с;
b = 1 м;
R = 2 м;
АО = 0 м;
MOZ = 50·t2 Н·м;
τ = 3 с;
ОК = (π·b/3)·(t1)2 м;
Т = 2 с
|
Продолжение табл..5.1
|
m1 = 24 кг;
m2 = 4 кг;
 = 4 рад/с;
b = 1 м;
АО = 0,5 м;
MOZ = – 27· = 4 рад/с;
b = 1 м;
АО = 0,5 м;
MOZ = – 27· 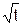 Н·м;
τ = 1 с;
ОК = 0,3·t1 м;
Т = 2 с Н·м;
τ = 1 с;
ОК = 0,3·t1 м;
Т = 2 с
| |
|
m1 = 40 кг;
m2 = 10 кг;
 = 2 рад/с;
R = 1 м;
АО = 0 м;
MOZ = 120·t Н·м;
τ = 1 с;
ОК = 0,5·t1 м;
Т = 3 с = 2 рад/с;
R = 1 м;
АО = 0 м;
MOZ = 120·t Н·м;
τ = 1 с;
ОК = 0,5·t1 м;
Т = 3 с
| |
|
m1 = 120 кг;
m2 = 50 кг;
 = – 4 рад/с;
b = 1 м;
R = 2 м;
АО = 0 м;
MOZ = 330·t2 Н·м;
τ = 2 с;
ОК = (π·b/2)·(t1)2 м;
Т = 1 с = – 4 рад/с;
b = 1 м;
R = 2 м;
АО = 0 м;
MOZ = 330·t2 Н·м;
τ = 2 с;
ОК = (π·b/2)·(t1)2 м;
Т = 1 с
|
Продолжение табл. 5.1
|
m1 = 60 кг;
m2 = 10 кг;
 = – 5 рад/с;
b = 1 м;
c = 1,2 м;
α = 30о;
АО = 0,4 м;
MOZ = 74 Н·м;
τ = 2 с;
ОК = 0,3·(t1)2 м;
Т = 2 с = – 5 рад/с;
b = 1 м;
c = 1,2 м;
α = 30о;
АО = 0,4 м;
MOZ = 74 Н·м;
τ = 2 с;
ОК = 0,3·(t1)2 м;
Т = 2 с
| |
|
m1 = 50 кг;
m2 = 10 кг;
 = – 2 рад/с;
R = 1,6 м;
α = 30о;
АО = 0,6 м;
MOZ = 69·t Н·м;
τ = 4 с;
ОК = 0,6·t1 м;
Т = 2 с = – 2 рад/с;
R = 1,6 м;
α = 30о;
АО = 0,6 м;
MOZ = 69·t Н·м;
τ = 4 с;
ОК = 0,6·t1 м;
Т = 2 с
| |
|
m1 = 120 кг;
m2 = 50 кг;
 = 3 рад/с;
b = 2 м;
c = 3 м;
R = 0,8 м;
АО = π·R/2 м;
MOZ = 324 Н·м;
τ = 3 с;
ОК = (π·R/8)·(t1)2 м;
Т = 2 с = 3 рад/с;
b = 2 м;
c = 3 м;
R = 0,8 м;
АО = π·R/2 м;
MOZ = 324 Н·м;
τ = 3 с;
ОК = (π·R/8)·(t1)2 м;
Т = 2 с
|
Продолжение табл. 5.1
|
m1 = 90 кг;
m2 = 30 кг;
 = 1 рад/с;
b = 1,5 м;
АО = 0 м;
MOZ = – 135·t Н·м;
τ = 2 с;
ОК= (π·b/4)·(t1)2 м;
Т = 1 с = 1 рад/с;
b = 1,5 м;
АО = 0 м;
MOZ = – 135·t Н·м;
τ = 2 с;
ОК= (π·b/4)·(t1)2 м;
Т = 1 с
| |

|
m1 = 50 кг;
m2 = 12 кг;
 = 3 рад/с;
b = 1 м;
R = 1,2 м;
АО = π·b/6 м;
MOZ = –14·t2 Н·м;
τ = 3 с;
ОК = (π·b/12)·(t1)2 м;
Т = 2 с = 3 рад/с;
b = 1 м;
R = 1,2 м;
АО = π·b/6 м;
MOZ = –14·t2 Н·м;
τ = 3 с;
ОК = (π·b/12)·(t1)2 м;
Т = 2 с
| |
|
m1 = 40 кг;
m2 = 10 кг;
 = – 6 рад/с;
R = 1 м;
АО = 0,707 м;
MOZ = 75· = – 6 рад/с;
R = 1 м;
АО = 0,707 м;
MOZ = 75·  Н·м;
τ = 1 с;
ОК = (1,41/16)·(t1)2 м;
Т = 2 с Н·м;
τ = 1 с;
ОК = (1,41/16)·(t1)2 м;
Т = 2 с
|
Продолжение табл..5.1
|
m1 = 150 кг;
m2 = 50 кг;
 = – 1 рад/с;
b = 1,6 м;
с = 1,2 м;
R = 0,6 м;
АО = π·R/2 м;
MOZ = 163 Н·м;
τ = 4 с;
ОК = (π·R/2)·(t1)2 м;
Т = 1 с = – 1 рад/с;
b = 1,6 м;
с = 1,2 м;
R = 0,6 м;
АО = π·R/2 м;
MOZ = 163 Н·м;
τ = 4 с;
ОК = (π·R/2)·(t1)2 м;
Т = 1 с
| |
|
m1 = 90 кг;
m2 = 20 кг;
 = 2 рад/с;
b = 1,414 м;
с = 1 м;
АО = 0,866 м;
MOZ = – 210 Н·м;
τ = 2 с;
ОК = 0,866·t1 м;
Т = 1 с = 2 рад/с;
b = 1,414 м;
с = 1 м;
АО = 0,866 м;
MOZ = – 210 Н·м;
τ = 2 с;
ОК = 0,866·t1 м;
Т = 1 с
| |
|
m1 = 50 кг;
m2 = 12 кг;
 = – 3 рад/с;
b = 0,6 м;
α = 60о;
АО = 0,2 м;
MOZ = 27·t2 Н·м;
τ = 2 с;
ОК = 0,4·t1 м;
Т = 2 с = – 3 рад/с;
b = 0,6 м;
α = 60о;
АО = 0,2 м;
MOZ = 27·t2 Н·м;
τ = 2 с;
ОК = 0,4·t1 м;
Т = 2 с
|
Продолжение табл. 5.1
|
m1 = 36 кг;
m2 = 8 кг;
 = – 5 рад/с;
R = 0,5 м;
АО = 0 м;
MOZ = 20·t Н·м;
τ = 2 с;
ОК = (π·R/6)·(t1)2 м;
Т = 2 с = – 5 рад/с;
R = 0,5 м;
АО = 0 м;
MOZ = 20·t Н·м;
τ = 2 с;
ОК = (π·R/6)·(t1)2 м;
Т = 2 с
| |
|
m1 = 150 кг;
m2 = 40 кг;
 = – 4 рад/с;
b = 1,5 м;
R = 2 м;
АО = π·b/6 м;
MOZ = 1170· = – 4 рад/с;
b = 1,5 м;
R = 2 м;
АО = π·b/6 м;
MOZ = 1170· 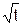 Н·м;
τ = 1 с;
ОК = (π·b/2)·(t1)2 м;
Т = 1 с Н·м;
τ = 1 с;
ОК = (π·b/2)·(t1)2 м;
Т = 1 с
| |
|
m1 = 120 кг;
m2 = 30 кг;
 = 0 рад/с;
b = 1 м;
α = 600;
АО = 0 м;
MOZ = – 25·t Н·м;
τ = 2 с;
ОК= (t1)2 м;
Т = 1 с = 0 рад/с;
b = 1 м;
α = 600;
АО = 0 м;
MOZ = – 25·t Н·м;
τ = 2 с;
ОК= (t1)2 м;
Т = 1 с
|
Окончание табл. 5.1
|
m1 = 15 кг;
m2 = 4 кг;
 = – 2 рад/с;
b = 0,6 м;
АО = 0,1 м;
MOZ = 5,6·t Н·м;
τ = 3 с;
ОК = 0,4·t1 м;
Т = 1 с = – 2 рад/с;
b = 0,6 м;
АО = 0,1 м;
MOZ = 5,6·t Н·м;
τ = 3 с;
ОК = 0,4·t1 м;
Т = 1 с
| |
|
m1 = 20 кг;
m2 = 5 кг;
 = 5 рад/с;
b = 0,6 м;
R = 0,6 м;
АО = 0 м;
MOZ = – 6,3· = 5 рад/с;
b = 0,6 м;
R = 0,6 м;
АО = 0 м;
MOZ = – 6,3· 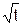 Н·м;
τ = 4 с;
ОК = (5·π·R/6)·t1 м;
Т = 1 с Н·м;
τ = 4 с;
ОК = (5·π·R/6)·t1 м;
Т = 1 с
| |
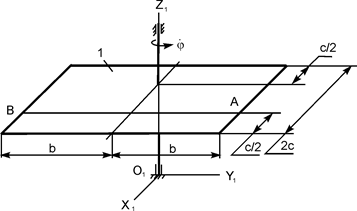
|
m1 = 150 кг;
m2 = 50 кг;
 = 0 рад/с;
b = 1,6 м;
с = 1,2 м;
АО = 1,6 м;
MOZ = 652·t Н·м;
τ = 2 с;
ОК = 0,2·(t1)2 м;
Т = 2 с = 0 рад/с;
b = 1,6 м;
с = 1,2 м;
АО = 1,6 м;
MOZ = 652·t Н·м;
τ = 2 с;
ОК = 0,2·(t1)2 м;
Т = 2 с
|
ПРИМЕЧАНИЕ. Знак минус перед MOZ и  соответствует направлению вращения часовой стрелки, если смотреть со стороны положительного направления оси OZ.
соответствует направлению вращения часовой стрелки, если смотреть со стороны положительного направления оси OZ.
5.3.6. Пример выполнения курсового задания Д 3
Условие задания.

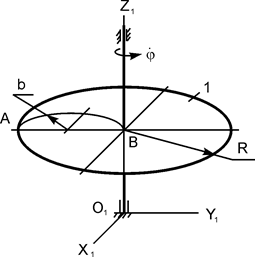
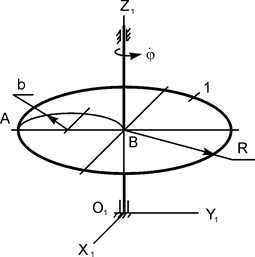
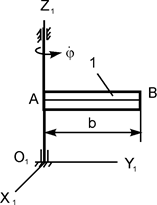
Тело Н массой m1 вращается вокруг вертикальной оси O1Z1 с постоянной угловой скоростью 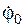 (рис. 5.12).
(рис. 5.12).
В точке О жёлоба АВ тела Н на расстоянии АО от точки А, отсчитываемом вдоль жёлоба, находится материальная точка К массой m2 (на рис. 5.12 точки О и К не показаны). В некоторый момент времени (t0 = 0) на систему начинает действовать пара сил с моментом MOZ = MOZ(t). При t = τ действие пары сил прекращается.
Определить значение угловой скорости  тела Н в момент времени t = τ (
тела Н в момент времени t = τ (  (τ) = ?).
(τ) = ?).
Тело Н вращается по инерции с угловой скоростью  (τ).
(τ).
В некоторый момент времени (t1 = 0, где t1 – новое начало отсчета времени) точка К (самоходный механизм) начинает относительное движение из точки О вдоль жёлоба АВ (в направлении от точки А к точке В) по закону ОК = S = S(t1).
Определить значение угловой скорости  тела Н в момент времени t1 = T (
тела Н в момент времени t1 = T (  (T) = ?).
(T) = ?).
Тело Н рассматривать как однородную пластинку.
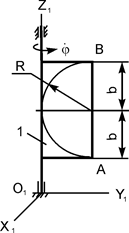
Дано: m1 = 20 кг; m2 = 5 кг; 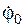 = 5 рад/с = const; b = 0,6 м; R = 0,6 м; АО = 0 м; MOZ = – 6,3·
= 5 рад/с = const; b = 0,6 м; R = 0,6 м; АО = 0 м; MOZ = – 6,3· 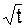 Н·м; τ = 4 с; OK = S(t1) = (5·π·R/6)·t1 м; Т = 1с.
Н·м; τ = 4 с; OK = S(t1) = (5·π·R/6)·t1 м; Т = 1с.
Решение.
К решению задачи применим теорему об изменении кинетического момента механической системы, выраженную уравнением
dLO1Z1/dt = ΣMO1Z1(  ) + ΣMO1Z1(
) + ΣMO1Z1(  ),
),
где LO1Z1 – кинетический момент механической системы относительно оси вращения; ΣMO1Z1(  ), ΣMO1Z1(
), ΣMO1Z1(  ) – соответственно суммы моментов активных сил и реакций внешних связей относительно оси вращения.
) – соответственно суммы моментов активных сил и реакций внешних связей относительно оси вращения.
Решение задачи разобьём на три этапа. На первом этапе рассмотрим движение механической системы в исходном положении; на втором этапе – движение этой системы в момент времени τ; на третьем этапе – движение механической системы в момент времени Т.
Первый этап.
В исходном положении тело Н (тело 1 массой m1), на котором неподвижно (на расстоянии АО = 0 м) установлено тело 2 (самоходный механизм массой m2), вращается с постоянной угловой скоростью  (см. рис. 5.12).
(см. рис. 5.12).
Введём неподвижную (инерциальную) систему отсчёта O1X1Y1Z1, совместив ось O1Z1 с осью вращения тела 1. Покажем на рис. 5.13 направление вращения тела 1 с произвольной угловой скоростью  .
.
Дата добавления: 2015-05-30; просмотров: 1302;
