Динамика движений твёрдого тела
5.4.1. Динамика поступательного движения твёрдого тела
Поступательным движением твёрдого тела называют такое его движение, при котором любая прямая линия, проведённая на теле, остается во всё время движения параллельной своему начальному положению.
Рассмотрим поступательное движение твёрдого тела на плоскости в инерциальной системе отсчёта OXYZ под действием активных сил  и реакций
и реакций  внешних связей (рис. 5.16).
внешних связей (рис. 5.16).

Из курса кинематики известно, что при поступательном движении твёрдого тела траектории всех его точек одинаковы (при наложении друг на друга траектории движения точек совпадают), а скорости и ускорения всех точек геометрически равны.
Эти свойства позволяют свести изучение поступательного движения твёрдого тела к изучению движения его отдельной точки. За такую точку, как правило, выбирают центр масс твёрдого тела.
Выражения XC = f1(t), YC = f2(t), ZC = f3(t), описывающие движение центра С масс твёрдого тела в пространстве, называют уравнениями поступательного движения твёрдого телав пространстве.
Твёрдое тело рассматривается как неизменяемая механическая система, в которой геометрическая сумма внутренних сил Σ  (главный вектор RJ внутренних сил) всегда равна нулю (Σ
(главный вектор RJ внутренних сил) всегда равна нулю (Σ  = RJ = 0).
= RJ = 0).
Таким образом, центр С масс твёрдого тела при его поступательном движении движется под действием активных сил  и реакций
и реакций  внешних связей.
внешних связей.
Основное уравнение динамики движения центра масс твёрдого тела имеет вид
m·aС = Σ  + Σ
+ Σ  =
= 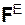 +
+ 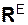 ,
,
где 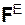 = Σ
= Σ  ,
, 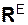 = Σ
= Σ  – главные векторы активных сил
– главные векторы активных сил  и реакций
и реакций  внешних связей.
внешних связей.
Главные векторы 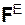 ,
, 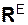 прикладывают в центре масс твёрдого тела.
прикладывают в центре масс твёрдого тела.
Как правило, основное уравнение динамики поступательного движения твёрдого тела записывают в виде
m·aС = Σ  + Σ
+ Σ  .
.
Произведение массы тела на ускорение его центра масс равно геометрической сумме активных сил и реакций внешних связей, приложенных к нему.
Спроецируем это векторное равенство на координатные оси неподвижной (инерциальной системы отсчёта) OXYZ:
m· 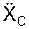 = Σ
= Σ  + Σ
+ Σ  ;
;
m· 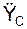 = Σ
= Σ  + Σ
+ Σ  ;
;
m· 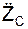 = Σ
= Σ  + Σ
+ Σ  ,
,
где m – масса тела; 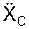 ,
, 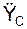 ,
, 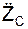 – проекции ускорения центра масс тела на координатные оси; Σ
– проекции ускорения центра масс тела на координатные оси; Σ  , Σ
, Σ  , Σ
, Σ  , Σ
, Σ  , Σ
, Σ  , Σ
, Σ  – суммы проекций соответственно активных сил и реакций внешних связей на координатные оси инерциальной системы отсчёта.
– суммы проекций соответственно активных сил и реакций внешних связей на координатные оси инерциальной системы отсчёта.
Последние выражения называют дифференциальными уравнениями поступательного движения твёрдого тела в пространстве.
По дифференциальным уравнениям поступательного движения твёрдого тела решают прямые и обратные задачи динамики. Алгоритмы решения таких задач не отличаются от алгоритмов решения задач динамики точки, приведённых в подразделах данного учебно-методического пособия, поэтому здесь они подробно не приводятся.
Так как курсовых заданий на решение дифференциальных уравнений поступательного движения твёрдого тела по учебной программе не предусмотрено, то и примеры решения таких задач здесь не приведены.
5.4.2. Динамика вращательного движения твёрдого тела
Вращательным движением твёрдого тела называется такое его движение, при котором все точки, находящиеся на прямой, неизменно связанной с телом и называемой осью вращения, остаются неподвижными.
Рассмотрим вращательное движение твёрдого тела в инерциальной системе отсчёта OXYZ под действием активных сил  и реакций
и реакций  внешних связей (рис. 5.17).
внешних связей (рис. 5.17).
При вращении тела угол его поворота φ изменяется в зависимости от времени t.
φ = f(t).
Эту аналитическую зависимость называют уравнением вращательного движения твёрдого тела. При вращательном движении твёрдого тела все его точки описывают окружности с центром на оси вращения и радиусом ri.
По известному уравнению φ = f(t) вращательного движения тела определяют его угловую скорость  и угловое ускорение
и угловое ускорение  .
.
 = dφ/dt;
= dφ/dt;  = d2φ/dt2.
= d2φ/dt2.
Согласно рис. 5.17 на рассматриваемую механическую систему (твёрдое тело) кроме активных сил  действуют реакции
действуют реакции  внешних связей. К этим реакциям отнесены: XA, YA, ZA, XB, YB,
внешних связей. К этим реакциям отнесены: XA, YA, ZA, XB, YB, 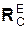 – соответственно реакции подпятника А, цилиндрического шарнира В и реакция тела другой механической системы в точке С.
– соответственно реакции подпятника А, цилиндрического шарнира В и реакция тела другой механической системы в точке С.
RE = Σ  = XA + YA + ZA + XB + YB +
= XA + YA + ZA + XB + YB + 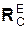 ,
,

где RE = Σ  – главный вектор реакций внешних связей.
– главный вектор реакций внешних связей.
Необходимо отметить, что в динамике твёрдое тело рассматривается как неизменяемая механическая система, в которой геометрическая сумма внутренних сил  (главный вектор RJ внутренних сил) всегда равна нулю (Σ
(главный вектор RJ внутренних сил) всегда равна нулю (Σ  = RJ = 0).
= RJ = 0).
С учетом этого дифференциальное уравнение вращательного движения твёрдого тела относительно оси вращения OZ имеет вид
JOZ·  = ΣMOZ(
= ΣMOZ(  ) + ΣMOZ(
) + ΣMOZ(  ),
),
где JOZ – момент инерции твёрдого тела относительно оси вращения; ΣMOZ(  ), ΣMOZ(
), ΣMOZ(  ) – соответственно суммы моментов активных сил и реакций внешних связей относительно оси вращения.
) – соответственно суммы моментов активных сил и реакций внешних связей относительно оси вращения.
Сравним дифференциальное уравнение вращательного движения твёрдого тела (JOZ·  = ΣMOZ(
= ΣMOZ(  ) + ΣMOZ(
) + ΣMOZ(  )) с одним из дифференциальных уравнений поступательного движения твёрдого тела (m·
)) с одним из дифференциальных уравнений поступательного движения твёрдого тела (m· 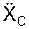 = Σ
= Σ  + Σ
+ Σ  ).
).
Очевидно, что момент инерции JOZ твёрдого тела при вращательном движении имеет то же значение, что и масса m при его поступательном движении.
Таким образом, момент инерции является мерой инертности тела при его вращательном движении.
По дифференциальному уравнению вращательного движения твёрдого тела (JOZ·  = ΣMOZ(
= ΣMOZ(  ) + ΣMOZ(
) + ΣMOZ(  )) решают следующие задачи:
)) решают следующие задачи:
1. По заданному уравнению движения φ = f(t) и его моменту инерции JOZ определяют главный момент 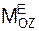 внешних сил, действующих на тело:
внешних сил, действующих на тело:
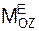 = ΣMOZ(
= ΣMOZ(  ) + ΣMOZ(
) + ΣMOZ(  ).
).
2. По заданным активным силам  и реакциям
и реакциям  внешних связей, а также по начальным условиям вращения (
внешних связей, а также по начальным условиям вращения ( 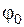 ,
, 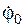 ) и по моменту инерции JOZ тела относительно оси вращения определяют уравнение движения φ = f(t).
) и по моменту инерции JOZ тела относительно оси вращения определяют уравнение движения φ = f(t).
3. Определяют момент инерции JOZ относительно оси вращения по известным величинам углового ускорения  и главного момента
и главного момента 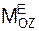 внешних сил, действующих на тело.
внешних сил, действующих на тело.
Поскольку учебной программой выполнение курсовых заданий на применение дифференциальных уравнений вращательного движения твёрдого тела не запланировано, то и примеры решения задач на эту тему в данном учебно-методическом пособии не приведены.
5.4.3. Динамика плоскопараллельного движения
твёрдого тела
Плоскопараллельным (плоским) движением твёрдого тела называется такое движение, при котором каждая точка тела движется в плоскости, параллельной некоторой неподвижной плоскости.

Рассмотрим плоскопараллельное движение твёрдого тела в инерциальной системе отсчёта OXY, происходящее под действием активных сил  и реакций
и реакций  внешних связей (рис. 5.18).
внешних связей (рис. 5.18).
Поскольку твёрдое тело рассмотрено как неизменяемая механическая система, то главный вектор RJ внутренних сил  , приложенных к точкам тела, всегда равен нулю (RJ = Σ
, приложенных к точкам тела, всегда равен нулю (RJ = Σ  = 0). Так как внутренние силы
= 0). Так как внутренние силы  не влияют на движение центра С масс тела, то они на рис. 5.18 не показаны.
не влияют на движение центра С масс тела, то они на рис. 5.18 не показаны.
Из курса кинематики известно, что плоскопараллельное движение можно рассматривать как сложное движение, представляющее собой сумму двух движений: 1 – поступательное движение со скоростью VC центра масс в неподвижной системе отсчёта OХY; 2 – вращательное движение относительно подвижной оси CZ1, проходящей через центр масс, при этом подвижная система отсчёта CX1Y1Z1 совершает поступательное движение.
Необходимо отметить, что начало системы отсчёта CX1Y1Z1 всегда располагают в центре С масс тела.
Уравнения плоскопараллельного движения твёрдого тела в динамике, как правило, записывают в следующем виде:
XC = f1(t); YC = f2(t); φ = f3(t).
С использованием этих уравнений движения дифференциальные уравнения плоскопараллельного движения твёрдого тела имеют вид:
m· 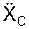 = Σ
= Σ  + Σ
+ Σ  ;
;
m· 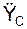 = Σ
= Σ  + Σ
+ Σ  ;
;
JСZ1·  = ΣMСZ1(
= ΣMСZ1(  ) + ΣMСZ1(
) + ΣMСZ1(  ),
),
где m – масса тела; 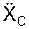 ,
, 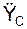 – проекции ускорения центра С масс тела на координатные оси неподвижной системы отсчёта OXY; Σ
– проекции ускорения центра С масс тела на координатные оси неподвижной системы отсчёта OXY; Σ  , Σ
, Σ  – суммы проекций активных сил
– суммы проекций активных сил  на координатные оси OX, OY; Σ
на координатные оси OX, OY; Σ  , Σ
, Σ  – суммы проекции реакций
– суммы проекции реакций  внешних связей на координатные оси OX, OY;
внешних связей на координатные оси OX, OY;  – угловое ускорение тела; JСZ1 – момент инерции твёрдого тела относительно подвижной оси CZ1 вращения, проходящей через центр масс; ΣMСZ1(
– угловое ускорение тела; JСZ1 – момент инерции твёрдого тела относительно подвижной оси CZ1 вращения, проходящей через центр масс; ΣMСZ1(  ), ΣMСZ1(
), ΣMСZ1(  ) – соответственно суммы моментов активных сил и реакций внешних связей относительно подвижной оси CZ1 вращения, проходящей через центр масс тела.
) – соответственно суммы моментов активных сил и реакций внешних связей относительно подвижной оси CZ1 вращения, проходящей через центр масс тела.
С помощью этих дифференциальных уравнений движения твёрдого тела можно решать как прямые (первые), так и обратные (вторые) задачи динамики.
При решении обратных задач динамики (определение движения по заданным силам) приходится интегрировать систему дифференциальных уравнений плоскопараллельного движения твёрдого тела. Для определения шести постоянных интегрирования (С1,…, С6) должны быть заданы шесть начальных условий движения: XC0, YC0, ZC0, 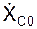 ,
, 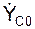 ,
, 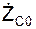 .
.
В учебной программе могут быть предусмотрены курсовые задания по излагаемой теме, поэтому необходимо привести алгоритм решения таких задач.
Решение задач динамики плоскопараллельного движения твёрдого тела рекомендуется выполнять по следующему алгоритму.
1. Выбрать неподвижную (инерциальную) систему отсчёта OXY.
2. Изобразить тело в системе отсчёта OXY в произвольный момент времени.
3. В центре С масс твёрдого тела разместить начало подвижной системы отсчёта.
4. Изобразить на рисунке все внешние силы (  ,
,  ), приложенные к твёрдому телу.
), приложенные к твёрдому телу.
5. Составить дифференциальные уравнения плоскопараллельного движения твёрдого тела:
m· 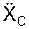 = Σ
= Σ  + Σ
+ Σ  ;
;
m· 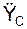 = Σ
= Σ  + Σ
+ Σ  ;
;
JСZ1·  = ΣMСZ1(
= ΣMСZ1(  ) + ΣMСZ1(
) + ΣMСZ1(  ).
).
Дальнейший ход решения зависит от того, какая задача динамики должна быть решена – прямая или обратная.
5.4.4. Динамика сферического движения твёрдого тела
Рассмотрим движение тела, одна из точек которого во всё время движения остается неподвижной. При таком движении все остальные точки тела движутся по сферическим поверхностям, центры которых совпадают с неподвижной точкой. Такое движение называют сферическим движением твёрдого тела.
Сферическое движение твёрдого тела – движение, при котором скорость одной точки тела равна нулю, а остальные точки движутся по сферическим поверхностям, центры которых совпадают с этой неподвижной точкой.
Примером сферического движения тела служит движение волчка, имеющего неподвижную точку О1 (рис. 5.19).
Для определения положения тела в каждый момент времени используют две системы отсчёта: неподвижную систему отсчёта O1X1Y1Z1 и подвижную систему отсчёта OXYZ, которая жёстко закреплена на теле. При этом начало отсчёта ПСО совпадает с началом отсчёта НСО.
На рис. 5.19 стрелками показаны положительные направления отсчёта углов Ψ, θ и φ. Рассмотрим подробнее порядок отсчёта этих углов. Плоскость OXY подвижной системы отсчёта OXYZ пересекается с плоскостью O1X1Y1 неподвижной системы отсчёта O1X1Y1Z1 по линии O1L. Эту линию называют осью узлов. Введём единичный вектор р, направленный от точки О1 к точке L оси узлов. Единичные векторы i1, p лежат в горизонтальной плоскости O1X1Y1 и образуют угол Ψ, величина которого зависит от времени. Ψ = f1(t). Положительное направление отсчёта угла Ψ определяют по правилу: смотря навстречу вектору k1, поворот вектора i1 к вектору р должны увидеть происходящим против хода часовой стрелки.

Единичные векторы k1, k образуют плоскость, в которой находится угол θ, который также зависит от времени: θ = f2(t). Положительное направление отсчёта угла θ определяют по правилу: смотря навстречу вектору i, поворот вектора k1 к вектору k должны увидеть происходящим против хода часовой стрелки.
Единичные векторы р, i образуют плоскость, в которой лежит угол φ, величина которого зависти от времени: φ = f3(t). Правило положительного направления отсчёта угла φ: смотря навстречу вектору j, поворот вектора р к вектору i должны увидеть происходящим против хода часовой стрелки.
Углы Ψ, θ, φ называют также эйлеровыми углами:
угол Ψ – угол прецессии;
угол θ – угол нутации;
угол φ – угол собственного вращения.
Так как положение тела, имеющего одну неподвижную точку, определяется тремя эйлеровыми углами, т. е. тремя параметрами, то оно имеет три степени свободы.
Таким образом, сферическое движение тела описывается тремя уравнениями движения:
Ψ = f1(t); θ = f2(t); φ = f3(t).
На твёрдое тело, совершающее сферическое движение, действуют активные силы  , реакция опоры
, реакция опоры 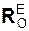 и внутренние силы
и внутренние силы 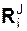 . Следует отметить, что активные силы
. Следует отметить, что активные силы  и реакцию опоры
и реакцию опоры 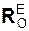 относятся к разряду внешних сил. При этом моменты реакции
относятся к разряду внешних сил. При этом моменты реакции 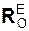 относительно координатных осей ОХ, OY, OZ системы отсчета OXYZ равны нулю.
относительно координатных осей ОХ, OY, OZ системы отсчета OXYZ равны нулю.
Для абсолютно твёрдого тела геометрическая сумма реакций внутренних связей всегда равна нулю ( 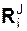 = 0). Исходя из этого утверждения, дифференциальные уравнения сферического движения твёрдого тела имеют вид:
= 0). Исходя из этого утверждения, дифференциальные уравнения сферического движения твёрдого тела имеют вид:
JОX· 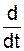 (
(  ·sin(θ)·sin(φ) +
·sin(θ)·sin(φ) +  ·cos(φ)) +
·cos(φ)) +
+ (  ·sin(θ)·cos(φ) –
·sin(θ)·cos(φ) –  ·sin(φ))·(
·sin(φ))·(  ·cos(θ) +
·cos(θ) +  )·(JОZ – JОY) =
)·(JОZ – JОY) =
= Σ MОX(  ); (1)
); (1)
JОY· 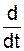 (
(  ·sin(θ)·cos(φ) –
·sin(θ)·cos(φ) –  ·sin(φ)) +
·sin(φ)) +
+ (  ·cos(θ) +
·cos(θ) +  )·(
)·(  ·sin(θ)·sin(φ) +
·sin(θ)·sin(φ) +  ·cos(φ)) (JОX – JОZ) =
·cos(φ)) (JОX – JОZ) =
= Σ MОY(  ); (2)
); (2)
JОZ· 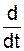 (
(  ·cos(θ) +
·cos(θ) +  ) +
) +
+ (  ·sin(θ)·sin(φ) +
·sin(θ)·sin(φ) +  ·cos(φ))·(
·cos(φ))·(  ·sin(θ)·cos(φ) –
·sin(θ)·cos(φ) –  ·sin(φ))×
·sin(φ))×
× (JОY – JОX) = Σ MОZ(  ), (3)
), (3)
где JОX, JОY, JОZ – моменты инерции тела относительно соответствующих координатных осей OX, OY, OZ системы отсчёта OXYZ;  – угловая скорость прецессии;
– угловая скорость прецессии;  – угловая скорость нутации;
– угловая скорость нутации;  – угловая скорость собственного вращения; Σ MOX(
– угловая скорость собственного вращения; Σ MOX(  ), Σ MOY(
), Σ MOY(  ),Σ MOZ(
),Σ MOZ(  ) – суммы моментов активных сил относительно координатных осей OX, OY, OZ системы отсчёта OXYZ.
) – суммы моментов активных сил относительно координатных осей OX, OY, OZ системы отсчёта OXYZ.
Дифференциальные уравнения сферического движения твёрдого тела называют динамическими уравнениями Эйлера.
Целью решения дифференциальных уравнений сферического движения твёрдого тела является получение зависимостей:
Ψ = f1(t); θ = f2(t); φ = f3(t).
Интегрирование динамических уравнений Эйлера связано с большими трудностями, поэтому выполнение студентами курсовых заданий на эту тему не предусмотрено.
5.4.5. Динамика общего случая движения твёрдого тела
В теоретической механике движение свободного тела в пространстве рассматривают как сложное, состоящее из поступательного движения со скоростью некоторой точки тела, принятой за полюс, и сферического движения вокруг этого полюса. Как правило, за полюс принимают центр С масс твёрдого тела (рис. 5.20).
Примем центр С масс за полюс и поместим в него начала двух подвижных систем отсчёта СXYZ, O2X2Y2Z2. Координатные оси CX, CY, CZ направляют по главным центральным осям инерции тела. При этом система отсчёта OXYZ неподвижно закреплена на теле, а система отсчёта O2X2Y2Z2 совершает поступательное движение таким образом, что её координатные оси параллельны координатным осям неподвижной системы отсчёта O1X1Y1Z1.
Плоскости OXY, O2X2Y2 подвижных систем отсчёта пересекаются по линии OL. Введением единичного вектора р эту линию преобразуют в ось узлов.
На рис. 5.20 показаны углы Ψ, φ, θ, величины которых зависят от времени. Эти углы называют эйлеровыми углами.
Таким образом, свободное движение тела определяется шестью уравнениями движения свободного твёрдого тела.
X1С = f1(t); Y1С = f2(t); Z1С = f3(t);
Ψ = f4(t); φ = f5(t); θ = f6(t),
где X1С, Y1С, Z1С – координаты центра масс тела в неподвижной системе отсчёта O1X1Y1Z1.

Свободное движение твёрдого тела осуществляется под действием активных сил  и реакций
и реакций 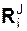 внутренних связей. Известно,, что для абсолютно твёрдого тела геометрическая сумма реакций внутренних связей равна нулю (
внутренних связей. Известно,, что для абсолютно твёрдого тела геометрическая сумма реакций внутренних связей равна нулю ( 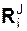 = 0). Исходя из этого утверждения, дифференциальные уравнения поступательной части свободного движения твёрдого тела имеют вид:
= 0). Исходя из этого утверждения, дифференциальные уравнения поступательной части свободного движения твёрдого тела имеют вид:
m· 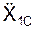 = Σ
= Σ 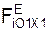 ; (1)
; (1)
m· 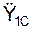 = Σ
= Σ  ; (2)
; (2)
m· 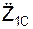 = Σ
= Σ 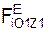 , (3)
, (3)
где m – масса тела; 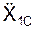 ,
, 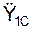 ,
, 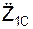 – проекции ускорения центра С масс тела на координатные оси системы отсчёта O1X1Y1Z1; Σ
– проекции ускорения центра С масс тела на координатные оси системы отсчёта O1X1Y1Z1; Σ 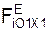 , Σ
, Σ  , Σ
, Σ 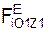 – суммы проекций активных сил
– суммы проекций активных сил  на координатные оси O1X1, O1Y1, O1Z1.
на координатные оси O1X1, O1Y1, O1Z1.
Сферическая часть движения твёрдого тела относительно центра масс описывается тремя дифференциальными уравнениями:
JCX· 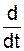 (
(  ·sin(θ)·sin(φ) +
·sin(θ)·sin(φ) +  ·cos(φ)) +
·cos(φ)) +
+ (  ·sin(θ)·cos(φ) –
·sin(θ)·cos(φ) –  ·sin(φ))·(
·sin(φ))·(  ·cos(θ) +
·cos(θ) +  )·(JCZ – JCY) =
)·(JCZ – JCY) =
= Σ MCX(  ); (4)
); (4)
JCY· 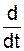 (
(  ·sin(θ)·cos(φ) –
·sin(θ)·cos(φ) –  ·sin(φ)) +
·sin(φ)) +
+ (  ·cos(θ) +
·cos(θ) +  )·(
)·(  ·sin(θ)·sin(φ) +
·sin(θ)·sin(φ) +  ·cos(φ)) (JCX – JCZ) =
·cos(φ)) (JCX – JCZ) =
= Σ MCY(  ); (5)
); (5)
JCZ· 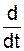 (
(  ·cos(θ) +
·cos(θ) +  ) +
) +
+ (  ·sin(θ)·sin(φ) +
·sin(θ)·sin(φ) +  ·cos(φ))·(
·cos(φ))·(  ·sin(θ)·cos(φ) –
·sin(θ)·cos(φ) –  ·sin(φ))×
·sin(φ))×
×(JCY – JCX) = Σ MCZ(  ), (6)
), (6)
где JCX, JCY, JCZ – моменты инерции тела относительно главных центральных осей инерции;  – угловая скорость прецессии;
– угловая скорость прецессии;  – угловая скорость нутации;
– угловая скорость нутации;  – угловая скорость собственного вращения; Σ MCX(
– угловая скорость собственного вращения; Σ MCX(  ),Σ MCY(
),Σ MCY(  ),Σ MCZ(
),Σ MCZ(  ) – суммы моментов активных сил относительно главных центральных осей.
) – суммы моментов активных сил относительно главных центральных осей.
Интегрирование дифференциальных уравнений (1) – (6) представляет большие трудности, поэтому для студентов заочной и дистанционной форм обучения выполнение курсовых заданий на свободное движение тела не предусмотрено.
Вопросы и задания для самоконтроля
1. Записать дифференциальные уравнения поступательного движения твёрдого тела в пространстве.
2. Записать дифференциальное уравнение вращательного движения твёрдого тела относительно вертикальной оси.
3. Записать дифференциальные уравнения плоскопараллельного движения твёрдого тела в системе отсчёта OXY.
Дата добавления: 2015-05-30; просмотров: 1885;
