Теорема об изменении кинетической энергии
5.5.1. Работа силы на перемещении точки её приложения
 |
Рассмотрим прямолинейное перемещение точки на горизонтальной плоскости OXY из положения М1 в положение М2, происходящее под действием постоянной силы F (рис. 5.21).
Работой A(F) постоянной силы на прямолинейном перемещении точки её приложения называется скалярное произведение вектора силы F на вектор U перемещения её точки приложения.
A(F) = F·U = F·U·cos(F, U) = F·U·cos(α),
где F – модуль силы F; U – модуль вектора U перемещения точки приложения силы F; α – угол, составленный направлениями векторов F и U.
Единица измерения работы [Н·м] = [Дж].
Согласно последнему равенству работа постоянной силы F на перемещении U точки её приложения равна произведению трёх сомножителей: модуля силы на модуль вектора перемещения точки приложения силы и на косинус угла, составленного направлениями векторов F и U.
 |
В зависимости от величины угла α работа A(F) силы F на перемещении U точки её приложения может быть положительной, отрицательной или равной нулю (рис. 5.22).
Анализ рис. 5.20 позволяет сделать следующие выводы:
1) если векторы F и U направлены в одну полуплоскость, то A(F) > 0;
2) если векторы F и U направлены в разные полуплоскости, то A(F) < 0;
3) если векторы F и U взаимно перпендикулярны, то A(F) = 0.
 |
Как правило, в задачах инженерной практики силы являются переменными, а точки их приложения описывают криволинейные траектории (рис. 5.23).
В этом случае используют понятие «элементарная работа силы».
Элементарная работа силы – скалярная мера действия силы, равная скалярному произведению силы на элементарное перемещение точки её приложения.
Рассмотренное понятие базируется на другом понятии – «элементарное перемещение точки».
Элементарное перемещение точки – перемещение точки из данного положения в положение, бесконечно близкое к нему.
Это перемещение изображается вектором, начало и конец которого совпадают соответственно с положениями точки в начале и конце перемещения. Элементарное перемещение dU направляется по касательной к траектории движения в данной точке. Так как вектор dU и вектор V скорости точки имеют одинаковое направление, то равенство для определения элементарной работы δA(F) имеет вид
δA(F) = F·dU = F·dU·cos(F, dU).
Работа переменной силы F на конечном перемещении U точки её приложения по произвольной траектории равна криволинейному интегралу, взятому вдоль кривой от точки М1 до точки М2 от элементарной работы δA.
А(F) = ∫F·dU = ∫F·dU·cos(F, dU).
Работа силы на конечном перемещении точки её приложения – величина, равная криволинейному интегралу от элементарной работы силы, действующей на данную материальную точку, взятому вдоль дуги кривой, описанной точкой при этом перемещении.
Если сила последовательно действует на разные точки механической системы (тела), то её работа при конечном перемещении системы определяется как предел суммы соответствующих элементарных работ.
Выражение работы переменной силы на конечном перемещении точки её приложения по криволинейной траектории через проекции FOX, FOY, FOZ силы F и проекции dX, dY, dZ вектора dU элементарного перемещения на оси декартовой системы отсчёта имеет вид
A(F) = ∫(FOX·dX + FOY·dY + FOZ·dZ).
 |
Рассмотрим движение i-й точки неизменяемой механической системы в инерциальной системе отсчёта OXYZ (рис. 5.24).
Как известно, точки механической системы осуществляют движение под действием активных сил  , реакций
, реакций  внешних связей и внутренних сил
внешних связей и внутренних сил  . В этом случае элементарная работа δAS внешних сил (
. В этом случае элементарная работа δAS внешних сил (  ,
,  ) и внутренних сил
) и внутренних сил  , приложенных к точке, будет равна
, приложенных к точке, будет равна
δAS = (  +
+  +
+  )·dU =
)·dU =
= 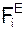 ·dU·cos(
·dU·cos(  , dU) +
, dU) + 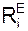 ·dU·cos(
·dU·cos(  , dU) +
, dU) + 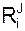 ·dU·cos(
·dU·cos(  , dU).
, dU).
 |
Определим работу силы тяжести G при перемещении точки из положения М1 в положение М2 в инерциальной системе отсчёта OXYZ (рис. 5.25).
Работу A(G) силы тяжести G определяют по формуле
A(G) = ± G·H,
где G – модуль силы тяжести (вес); Н – изменение высоты точки при её перемещении из положения М1 в положение М2.
Знак (+) соответствует перемещению точки вниз, а знак (–) соответствует перемещению точки вверх.
Таким образом, работа силы тяжести равна взятому со знаком (+) или (–) произведению модуля силы тяжести на вертикальное перемещение точки её приложения.
Работа силы тяжести не зависит от вида траектории, по которой перемещается точка её приложения, а зависит лишь от расстояния между горизонтальными плоскостями, проходящими через начальное и конечное положения точки.
В данном учебно-методическом пособии рассматриваются только неизменяемые механические системы. Для таких систем элементарная работа δAS(  ) внутренних сил, определяемая как сумма элементарных работ внутренних сил, действующих на точки, равна нулю.
) внутренних сил, определяемая как сумма элементарных работ внутренних сил, действующих на точки, равна нулю.
δAS(  ) = Σ
) = Σ 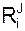 ·dU·cos(
·dU·cos(  , dU) = 0.
, dU) = 0.
Исходя из этого, элементарную работу δAS при перемещении неизменяемой механической системы определяют по формулам:
δAS = Σ(  +
+  )·dU;
)·dU;
δAS = Σ 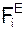 ·dU·cos(
·dU·cos(  , dU) + Σ
, dU) + Σ 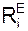 ·dU·cos(
·dU·cos(  , dU).
, dU).
В процессе движения механической системы её тела осуществляют три вида движений: поступательное, вращательное, плоскопараллельное.
При поступательном движении твёрдого тела, рассматриваемого как неизменяемая механическая система, элементарная работа δАS внешних сил, приложенных к нему, равна
δAS = Σ 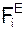 ·dU·cos(
·dU·cos(  , dU) + Σ
, dU) + Σ 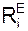 ·dU·cos(
·dU·cos(  , dU).
, dU).
При вращательном движении тела относительно оси OZ имеем
δAS = ΣMOZ(  )·δφ + ΣMOZ(
)·δφ + ΣMOZ(  )·δφ,
)·δφ,
где ΣMOZ(  ), ΣMOZ(
), ΣMOZ(  ) – соответственно моменты активных сил
) – соответственно моменты активных сил  и реакций
и реакций  внешних связей относительно оси OZ вращения тела; δφ – элементарный угол поворота тела (приращение угла поворота тела).
внешних связей относительно оси OZ вращения тела; δφ – элементарный угол поворота тела (приращение угла поворота тела).
Так как плоскопараллельное движение твёрдого тела есть сумма поступательного движения со скоростью полюса (как правило, за полюс принимают центр масс твёрдого тела) и вращательного движения с угловой скоростью  относительно оси, проходящей через полюс, то элементарную работу δAS определяют по формуле
относительно оси, проходящей через полюс, то элементарную работу δAS определяют по формуле
δAS = Σ 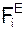 ·dUС·cos(
·dUС·cos(  , dUС) + Σ
, dUС) + Σ 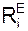 ·dUС·cos(
·dUС·cos(  , dUС) +
, dUС) +
+ ΣMCZ(  )·δφ +ΣMCZ(
)·δφ +ΣMCZ(  )·δφ,
)·δφ,
где ΣMCZ(  ), ΣMCZ(
), ΣMCZ(  ) – соответственно суммы моментов активных сил и реакций внешних связей относительно оси CZ , проходящей через центр масс тела; dUC – элементарное перемещение центра масс тела.
) – соответственно суммы моментов активных сил и реакций внешних связей относительно оси CZ , проходящей через центр масс тела; dUC – элементарное перемещение центра масс тела.
В инженерных дисциплинах широко используется понятие «мощность силы». Определим это понятие.
Мощность силы – величина, равная скалярному произведению силы на скорость точки её приложения.
Мощность обозначают символом N и находят по формуле
N = F·V = F·V·cos(F, V).
Так как мощность силы характеризует быстроту выполнения работы, то величину мощности можно находить по формуле
N = δA(F)/dt,
где δA(F) – элементарная работа силы; dt – промежуток времени, за который совершена элементарная работа.
Единица измерения мощности [Дж/с] = [Вт], (Bатт).
Для поступательного движения твёрдого тела мощность определяют по формуле
N = Σ 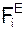 ·VС·cos(
·VС·cos(  , VС) + Σ
, VС) + Σ 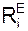 ·VС·cos(
·VС·cos(  , VС),
, VС),
где VС = dUС/dt – скорость центра масс.
При вращательном движении твёрдого тела имеем
N = ΣMOZ(  )·
)·  + ΣMOZ(
+ ΣMOZ(  )·
)·  ,
,
где  – угловая скорость вращения тела.
– угловая скорость вращения тела.
Вычисление суммы работ сил осуществляют по следующему алгоритму.
1. Изобржают на рисунке силы, приложенные к материальной точке либо к системе материальных точек.
2. Изображают элементарные перемещения точек системы.
3. Вычисляют элементарную работу сил, т. е. сумму работ всех сил на элементарных перемещениях точек системы.
4. Вычисляют искомую сумму работ сил на конечных перемещениях как сумму определённых интегралов, взятых в соответствующих пределах от элементарных работ. При наличии сил тяжести вычисляют работу этих сил на конечных перемещениях по формуле A(Gi) = ±Gi·HСi, где HСi – высота, на которую перемещается центр Сi масс i-го тела.
5.5.2. Кинетическая энергия механической системы
В динамике рассматриваются два случая преобразования механического движения материальной точки или системы точек.
1. Механическое движение переносится с одной механической системы на другую в качестве механического движения.
2. Механическое движение превращается в другую форму движения материи (в форму потенциальной энергии, теплоты, электричества и т. д.).
Каждый из этих случаев преобразования механического движения имеет свои измерители как механического движения, так и действия силы.
Когда рассматривается преобразование механического движения без перехода его в другую форму движения, мерой механического движения является вектор количества движения материальной точки K = m·V или механической системы K = m·VС. Мерой действия силы в этом случае является вектор S импульса силы.
Когда механическое движение превращается в другую форму движения материи, в качестве меры механического движения выступает кинетическая энергия материальной точки или механической системы.
Кинетическая энергия материальной точки – скалярная мера механического движения, равная половине произведения массы точки на квадрат её скорости движения.
Кинетическую энергию Т точки определяют по формуле
T = m·V2/2.
Мерой действия силы при превращении механического движения в другую форму движения является работа силы.
 |
Рассмотрим движение неизменяемой механической системы в инерциальной системе отсчёта OXYZ (рис. 5.26).
На рис. 5.26 использованы следующие обозначения: mCi, VCi – соответственно масса и скорость центра масс i-й точки механической системы; m, VC – масса и скорость центра масс механической системы.
Кинетическая энергия системы – величина, равная сумме кинетических энергий всех материальных точек механической системы.
Кинетическую энергию механической системы ТS определяют по формуле
ТS = Σ Тi,
где Тi – кинетическая энергия i-й точки механической системы.
Тела, входящие в механическую систему, осуществляют следующие виды движений: поступательное, вращательное, плоскопараллельное. Определим кинетические энергии тел, находящихся в этих движениях.
Рассмотрим поступательное движение твёрдого тела в инерциальной системе отсчёта OXYZ (рис. 5.27).
Кинетическую энергию тела при таком движении определяют по формуле
T = m·(VC)2/2,
где VC – скорость центра С масс тела.
Кинетическая энергия твёрдого тела, совершающего поступательное движение, равна половине произведения массы тела на квадрат скорости его центра масс.

При вращательных движениях тел (рис. 5.28) относительно различных осей (OX, OY, ОZ) кинетическую энергию определяют по формулам:
T = JOX· 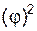 /2; T = JOY·
/2; T = JOY· 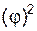 /2; T = JOZ·
/2; T = JOZ· 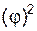 /2,
/2,
где JOX, JOY, JOZ – соответственно моменты инерции относительно осей вращения OX, OY, OZ;  – угловая скорость вращения тела.
– угловая скорость вращения тела.

Кинетическая энергия твёрдого тела, совершающего вращательное движение, равна половине произведения его момента инерции относительно соответствующей оси на квадрат угловой скорости.
 |
Как известно из кинематики, плоскопараллельное движение состоит из двух простейших движений: 1 – поступательное движение со скоростью VС центра масс в неподвижной (инерциальной) системе отсчёта OXY; 2 – вращательное движение с угловой скоростью
 относительно подвижной оси CZ1 вращения, проходящей через центр масс (рис. 5.29).
относительно подвижной оси CZ1 вращения, проходящей через центр масс (рис. 5.29).
Исходя из изложенного, кинетическую энергию тела при плоскопараллельном движении определяют по формуле
T = m·(VC)2/2 + JCZ1· 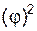 /2,
/2,
где JCZ1 – момент инерции тела относительно оси CZ1, проходящей через его центр масс.
Зависимость между изменением кинетической энергии неизменяемой механической системы и работой приложенных к её точкам сил на некотором перемещении определяется формулой
ТSk – ТSn = Σ 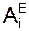 = ΣА(FiE) + ΣA(RiE),
= ΣА(FiE) + ΣA(RiE),
где ТSk – кинетическая энергия механической системы в конечном положении;ТSn – кинетическая энергия механической системы в исходном положении; Σ 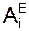 – сумма работ внешних сил (активных сил и реакций внешних связей) на перемещении механической системы из начального положения в конечное положение; ΣА(FiE) – сумма работ активных сил на перемещении механической системы; ΣA(RiE) – сумма работ реакций внешних связей на перемещении механической системы.
– сумма работ внешних сил (активных сил и реакций внешних связей) на перемещении механической системы из начального положения в конечное положение; ΣА(FiE) – сумма работ активных сил на перемещении механической системы; ΣA(RiE) – сумма работ реакций внешних связей на перемещении механической системы.
Эта формула выражает теорему об изменении кинетической энергии механической системы.
Изменение кинетической энергии неизменяемой механической системы на некотором перемещении равно сумме работ активных сил и реакций внешних связей, приложенных к системе, на этом же перемещении.
Для закрепления изложенного теоретического материала учебным планом рекомендуется выполнить курсовое задание Д 4.
5.5.3. Варианты курсового задания Д 4
«Применение теоремы об изменении
кинетической энергии к изучению движения
механической системы»
Механическая система под действием сил тяжести приходит в движение из состояния покоя; начальное положение системы показано в табл. 5.2. Учитывая трение скольжения тела 1 (варианты 1 – 3, 5, 6, 8 –1 2, 17 – 23, 29, 30) и пренебрегая другими силами сопротивления и массами нитей, предполагаемых нерастяжимыми, определить скорость центра масс С1 тела 1 в тот момент времени, когда пройденный им путь станет равным SС1.
В задании приняты следующие обозначения: m1, m2, m3, m4 – массы тел 1, 2, 3, 4; R2, r2, R3, r3 – радиусы больших и малых окружностей; iС2X2, iС3X3, iС4X4 – радиусы инерции ступенчатых колёс 2. 3 и 4 относительно горизонтальных осей, проходящих через их центры масс; α, β – углы наклона плоскостей к горизонту; f – коэффициент трения скольжения.
Расчётные схемы механизмов и необходимые для решения данные приведены в табл. 5.2. Блоки и катки, для которых радиусы инерции в таблице не указаны, считать сплошными однородными дисками.
Наклонные участки нитей параллельны соответствующим наклонным плоскостям.
Примечания к вариантам.
Вариант 4 – массами звеньев АВ, ВС3 и ползуна В пренебречь.
Вариант 5 – массой водила 5 пренебречь.
Вариант 14 – массы каждого из четырёх колес одинаковы.
Вариант 16 – массой водила 5 пренебречь.
Вариант 17 – шатун 3 рассматривать как тонкий однородный стержень.
Вариант 18 – массой водила 4 пренебречь.
Вариант 20 – массами звеньев АВ, ВС3 и ползуна В пренебречь.
Вариант 22 – массой водила 4 пренебречь.
Вариант 24 – массами звеньев АВ, ВС3 и ползуна В пренебречь.
Вариант 25 – массой водила пренебречь.
Вариант 26 – массы и моменты инерции колёс 2 и 5 одинаковы. Шатун 3 рассматривать как тонкий однородный стержень.
Вариант 28 – шатун 3 рассматривать как тонкий однородный стержень.
Таблица 5.2
| Номер варианта | Расчётная схема механизма | Исходные данные |
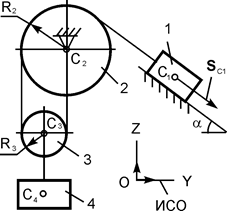
| m1 = m кг; m2 = 4·m кг; m3 = m/5 кг; m4 = 4·m/3 кг; α = 60о; f = 0,1; SС1 = 2 м | |
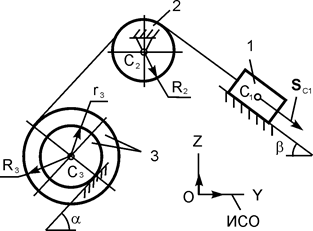
| m1 = m кг; m2 = m/2 кг; m3 = m/3 кг; R3 = 30 см; r3 = (2/3)·R3; iC3X3 = 20 см; α = 30о; β = 45о; f = 0,22; SС1 = 2 м | |
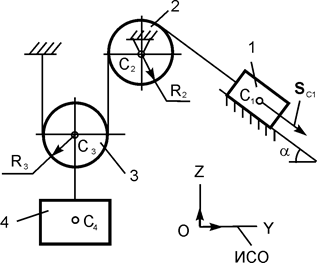
| m1 = m кг; m2 = m кг; m3 = m/10 кг; m4 = m кг; α = 45о; f = 0,10; SС1 = 2 м |
Продолжение табл..5.2
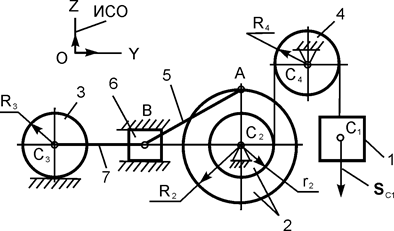
| m1 = m кг; m2 = 2·m кг; m3 = 40·m кг; m4 = m кг; R2 = 20 см; AB = 5·R2; R3 = 40 см; r2 = 0,5·R2; R4 = r2; iC2X2 = 18 см; SС1 = 0,1·π м | |
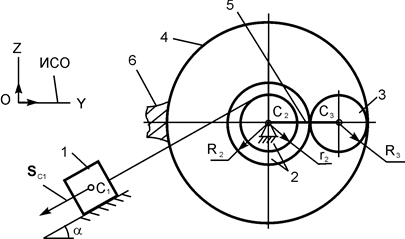
| m1 = m кг; m2 = 2·m кг; m3 = m кг; R3 = 20 см; R2 = 20 см; r2 = 0,8·R2; iC2X2 = 18 см; α = 60о; f = 0,12; SС1 = 0,28·π м | |
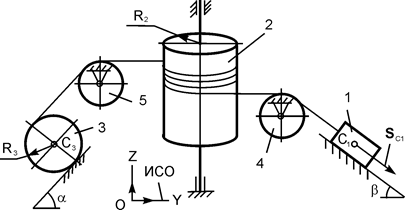
| m1 = m кг; m2 = 3·m кг; m3 = m кг; R3 = 28 см; α = 30о; β = 45о; f = 0,10; SС1 = 1,5 м |
Продолжение табл..5.2
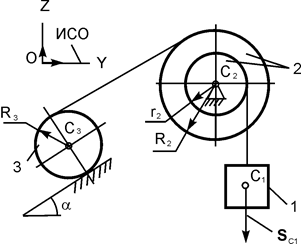
| m1 = m кг; m2 = 2·m кг; m3 = 2·m кг; R2 = 16 см; r2 = (3/4)·R2; R3 = 25 см; iC2X2 = 14 см; α = 30о; SС1 = 2 м | |

| m1 = m кг; m2 = m/2 кг; m3 = m/3 кг; R3 = 30 см; α = 30о; β = 45о; f = 0,15; SС1 = 1,75 м | |

| m1 = m кг; m2 = 2·m кг; m3 = 9·m кг; R3 = 30 см; r3 = 0,5·R3; iC3X3 = 20 см; α = 30о; f = 0,12; SС1 = 1,5 м |
Продолжение табл..5.2
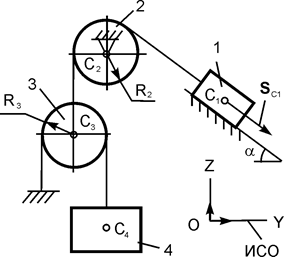
| m1 = m кг; m2 = m/4 кг; m3 = m/4 кг; m4 = m/5 кг; α = 60о; f = 0,10; SС1 = 3 м | |
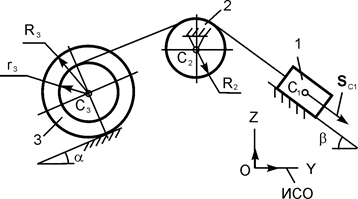
| m1 = m кг; m2 = m/2 кг; m3 = m/4 кг; R3 = 30 см; r3 = (2/3)·R3; iC3X3 = 25 см; α = 30о; β = 45о; f = 0,17; SС1 = 2,5 м | |
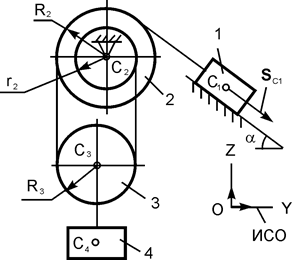
| m1 = m кг; m2 = m/2 кг; m3 = m/5 кг; m4 = m кг; R2 = 30 см; r2 = 20 см; iC2X2 = 25 см; α = 30о; f = 0,20; SС1 = 2,5 м |
Продолжение табл..5.2
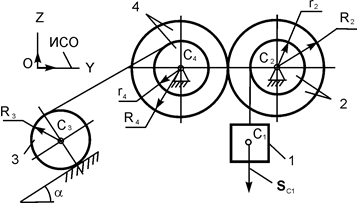
| m1 = m кг; m2 = 2·m кг; m3 = 5·m кг; m4 = 2·m кг; R2 = 30 см; R3 = 20 см; r2 = 0,8·R2; R4 = R2; r4 = 0,2·R4; iC2X2 = 26 см; iC4X4 = 0,5·iC2X2; α = 30о; SС1 = 2 м | |
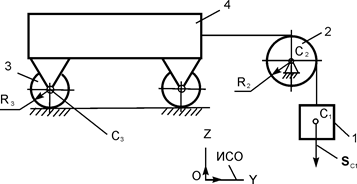
| m1 = m кг; m2 = m/2 кг; m3 = 5·m кг; m4 = 4·m кг; R3 = 25 см; SС1 = 2 м | |
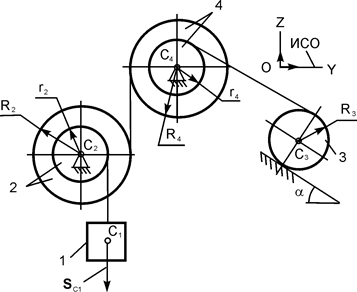
| m1 = m кг; m2 = m/2 кг; m3 = 4·m кг; m4 = m/2 кг; R2 = 20 см; R3 = 15 см; R4 = R2; r4 = r2 = 0,5·R2; iC4X4 = iC2X2; iC2X2 = 18 см; α = 60о; SС1 = 1,5 м |
Продолжение табл..5.2
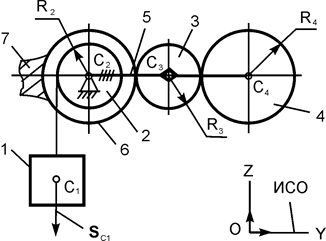
| m1 = m кг; m2 = 0,1·m кг; m3 = 0,2·m кг; m4 = 0,1·m кг; R2 = 10 см; R3 = 12 см; OC = 6 R3; R4 = 2·R3; SС1 = 0,05·π м | |
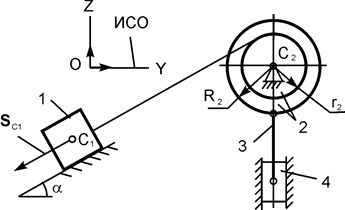
| m1 = m кг; m2 = m/4 кг; m3 = m/5 кг; m4 = 0,1·m кг; R2 = 20 см; r2 = 0,8·R2; iC2X2 = 15 см; α = 60о; f = 0,10; SС1 = 0,16·π м | |
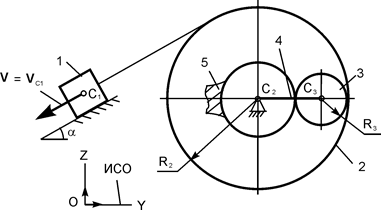
| m1 = m кг; m2 = 3·m кг; m3 = m кг; R3 = 20 см; R2 = 30 см; α = 60о; f = 0,15; SС1 = 0,2·π м |
Продолжение табл..5.2
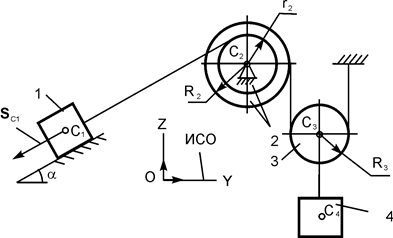
| m1 = m кг; m2 = m/3 кг; m3 = 0,1·m кг; m4 = m кг; R2 = 24 см; r2 = 0,8 R2; iC2X2 = 20 см; α = 60о; f = 0,15; SС1 = 1,5 м | |
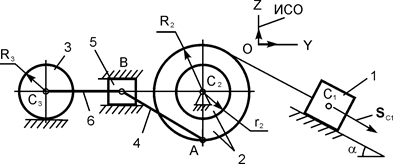
| m1 = m кг; m2 = 2·m кг; m3 = 20·m кг; R2 = 24 см; r2 = 0,5·R2; R3 = 15 см; iC2X2 = 16 см; AB = 6·R2; α = 30о; f = 0,10; SС1 = 0,2·π м | |
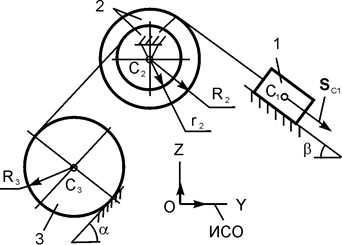
| m1 = m кг; m2 = m кг; m3 = 2·m кг; R2 = 20 см; r2 = (3/4)·R2; R3 = 20 см; iC2X2 = 16 см; α = 30о; β = 45о; f = 0,20; SС1 = 1,2 м |
Продолжение табл..5.2
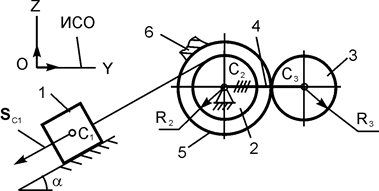
| m1 = m кг; m2 = m/2 кг; m3 = m/4 кг; R2 = 20 см; OC = 2·R2; R3 = 10 см; α = 60о; f = 0,17; SС1 = 0,1·π м | |
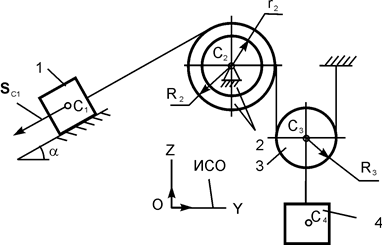
| m1 = m кг; m2 = m кг; m3 = 0,1·m кг; m4 = 0,8·m кг; R2 = 20 см; r2 = 0,8·R2; iC2X2 = 18 см; α = 30о; f = 0,10; SС1 = 1 м | |
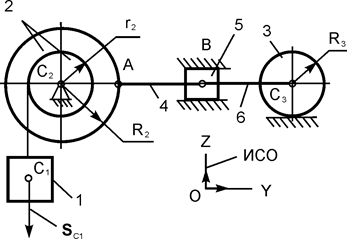
| m1 = m кг; m2 = 3·m кг; m3 = 20·m кг; R2 = 20 см; r2 = 0,8·R2; R3 = 30 см; iC2X2 = 18 см; AB = 4·R2; SС1 = 0,08·π м |
Продолжение табл..5.2
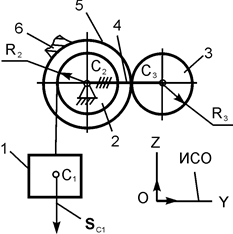
| m1 = m кг; m2 = m/3 кг; m3 = m/4 кг; R2 = 16 см; OC = 2,5·R2; R3 = 20 см; SС1 = 0,04·π м | |
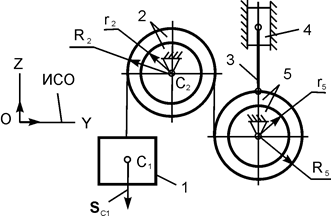
| m1 = m кг; m2 = m/2 кг; m3 = m кг; m4 = m/3 кг; R2 = 30 см; iC2X2 = 20 см; iC5X5 = 20 см; R2 = R5; r2 = r5 = 0,5·R2; SС1 = 0,6·π м | |
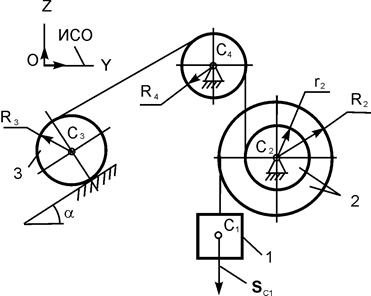
| m1 = m кг; m2 = m кг; m3 = 6·m кг; m4 = m/2 кг; R2 = 20 см; R3 = 20 см; iC2X2 = 16 см; α = 30о; SС1 = 2 м |
Окончание табл. 5.2
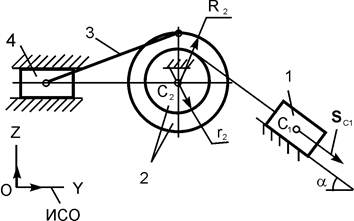
| m1 = m кг; m2 = 2·m кг; m3 = 3·m кг; R2 = 20 см; r2 = 0,5·R2; iC2X2 = 14 см; α = 60о; f = 0,10; SС1 = 0,1·π м | |
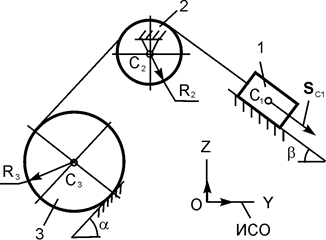
| m1 = m кг; m2 = m/5 кг; m3 = m/8 кг; R3 = 35 см; α = 15о; β = 30о; f = 0,20; SС1 = 2,4 м | |
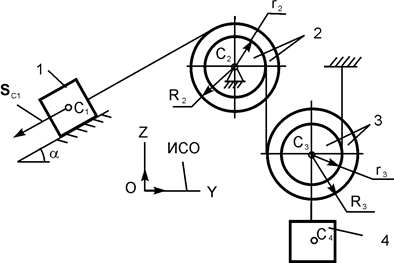
| m1 = m кг; m2 = m/2 кг; m3 = 0,3·m кг; m4 = 1,5·m кг; R2 = 26 см; R3 = 20 см; iC2X2 = 20 см; iC3X3 = 18 см; α = 30о; f = 0,12; SС1 = 2 м |
5.5.4. Пример выполнения курсового задания Д 4
Рассмотрим пример выполнения задания Д 4.
Условие задания.

Механическая система под действием сил тяжести приходит в движение из состояния покоя. Начальное положение системы показано на рис. 5.30.
Учитывая трение скольжения тела 1, пренебрегая силами сопротивления и массами нитей, предполагаемых нерастяжимыми, определить модуль скорости центра масс тела 1 в тот момент времени, когда пройденный им путь станет равным SС1.
В задании приняты следующие обозначения: m1, m2, m3, m4 – массы тел 1, 2, 3, 4; R2, r2, R3, r3 – радиусы больших и малых окружностей; iC2X2, iC3X3 – радиусы инерции тел 2 и 3 относительно горизонтальных осей, проходящих через их центры масс; α – угол наклона шероховатой поверхности к горизонту; f – коэффициент трения скольжения.
Дано: m1 = m; m2 = m/2; m3 = 0,3·m; m4 = 1,5·m; R2 = 26 см; r2 = 0,5·R2; R3 = 20 см; r3 = 0,5·R3; iC2X2 = 20 см; iC3X3 = 18 см; α = 30о; f = 0,12; SС1 = 2 м.
Курсовое задание рекомендуется выполнять по следующему алгоритму.
1. Записать теорему об изменении кинетической энергии неизменяемой механической системы на конечном перемещении.
TSk – TSn = Σ 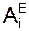 = ΣA(FiE) + ΣA(RiE),
= ΣA(FiE) + ΣA(RiE),
где TSk – значение кинетической энергии механической системы в конечный момент времени; TSn – значение кинетической энергии механической системы в начальный момент времени; Σ 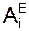 – сумма работ внешних сил, приложенных к механической системе на её конечном перемещении; ΣA(FiE) – сумма работ активных сил; ΣA(RiE) – сумма работ реакций внешних связей.
– сумма работ внешних сил, приложенных к механической системе на её конечном перемещении; ΣA(FiE) – сумма работ активных сил; ΣA(RiE) – сумма работ реакций внешних связей.
2. Определить кинетическую энергию TSn механической системы в начальный момент времени. Поскольку механическая система движется из состояния покоя (см. рис. 5.30), то во всех вариантах заданий имеем TSn = 0.
3. Изобразить на рисунке механическую систему в момент времени, когда центр С1 масс тела 1 проходит расстояние S (см. рис. 5.31).

4. Провести кинематический анализ безаварийной работы исследуемой механической системы.
Согласно рис. 5.31 тела механической системы осуществляют следующие виды движений. Тело 1 – поступательное движение со скоростью VC1 центра С1 его масс; тело 2 – вращательное движение с угловой скоростью  относительно оси вращения С2Х2, проходящей через центр масс С2; тело 3 – плоскопараллельное движение; тело 4 – поступательное движение со скоростью VC4 центра С4 его масс.
относительно оси вращения С2Х2, проходящей через центр масс С2; тело 3 – плоскопараллельное движение; тело 4 – поступательное движение со скоростью VC4 центра С4 его масс.
5. Выразить модули скоростей центров масс и угловых скоростей тел механической системы в зависимости от VC1 модуля скорости центра С1 масс тела 1.
С целью сокращения формы записи введём обозначение V = VC1. При определении кинематических характеристик тел механической системы учтём, что в точках контакта тел модули скоростей этих точек должны быть одинаковыми из условия их принадлежности соприкасающимся телам.
Итак, необходимо определить зависимости: I  I = ω2 = f1(V), VC3 = f2(V), I
I = ω2 = f1(V), VC3 = f2(V), I 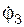 I = ω3 = f3(V), VC4 = f4(V), где ω2, ω3 – модули угловых скоростей
I = ω3 = f3(V), VC4 = f4(V), где ω2, ω3 – модули угловых скоростей  ,
, 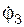 тел 2 и 3 .
тел 2 и 3 .
Так как тело 1 совершает поступательное движение, а нить нерастяжима, то справедливо равенство
VC1 = V = VA = VB,
где VA – модуль скорости точки А контакта тела 1 с нитью; VB – модуль скорости точки В контакта нити с телом 2.
Из условия принадлежности точки В телу 2, совершающему вращательное движение с угловой скоростью  относительно оси вращения С2Х2, проходящей через центр масс С2, имеем
относительно оси вращения С2Х2, проходящей через центр масс С2, имеем
VВ = V = ω2·BC2 = ω2·R2.
Отсюда получим
ω2 =  =
= 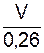 = 3,846·V.
= 3,846·V.
Зная модуль ω2 угловой скорости  , несложно определить модуль VE скорости точки Е соприкосновения тела 2 с участком ЕК нерастяжимой нити.
, несложно определить модуль VE скорости точки Е соприкосновения тела 2 с участком ЕК нерастяжимой нити.
VE = ω2·EC2 = ω2·r2 =  ·r2 =
·r2 =  ·0,5·R2 = 0,5·V.
·0,5·R2 = 0,5·V.
Зависимости, связывающие модули скоростей точек B, C, E, несложно получить и из рассмотрения подобия треугольников на рис. 5.31.
Модуль VK скорости точки К контакта нити с телом 3 равен модулю VE скорости точки Е нити.
VK = VE = 0,5·V.
Из условия принадлежности точки К телу 3, совершающему плоскопараллельное движение, справедливо равенство
VK = 0,5·V = ω3·КР3,
где ω3 – модуль угловой скорости 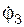 тела 3; КР3 – расстояние от точки К до мгновенного центра скоростей – точки Р3.
тела 3; КР3 – расстояние от точки К до мгновенного центра скоростей – точки Р3.
Согласно рис. 5.31 имеем KP3 = R3 + r3. Тогда
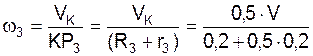 = 1,666·V.
= 1,666·V.
Модуль VC3 скорости центра С3 масс тела 3 равен
VC3 = ω3·C3P3 = ω3·r3 = 1,666·V·(0,5·0,2) = 0,166·V.
Так как по условию задания нити нерастяжимы, то легко видеть, что модуль VC3 скорости центра масс тела 3 равна модулю VC4 скорости центра С4 масс тела 4.
VC4 = VC3 = 0,166·V.
Таким образом, зависимости ω2 = f1(V), VC3 = f2(V), ω3 = f3(V), VC4 = f4(V) получены.
6. Определить кинетическую энергию TSk неизменяемой механической системы в её конечном положении по формуле
TSk = ΣTSki,
где TSki – кинетическая энергия i-го тела системы в конечном положении.
Кинетическая TSk1 энергия тела 1, совершающего поступательное движение,
TSk1 = 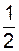 ·m1·(VC1)2 =
·m1·(VC1)2 = 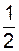 ·m·V2 = 0,5·m·V2.
·m·V2 = 0,5·m·V2.
Кинетическая TSk2 энергия тела 2 при его вращательном движении находится по формуле
TSk2 = 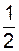 ·JC2X2·(ω2)2 =
·JC2X2·(ω2)2 = 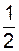 ·(m2·(iC2X2)2)·(ω2)2 =
·(m2·(iC2X2)2)·(ω2)2 =
= 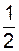 ·((m/2)·(iC2X2)2)·(V/R2)2 =
·((m/2)·(iC2X2)2)·(V/R2)2 =
= 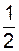 ·((m/2)·(0,2)2)·(V/0,26)2 = 0,147·m·V2.
·((m/2)·(0,2)2)·(V/0,26)2 = 0,147·m·V2.
Кинетическая энергия тела 3 при его плоскопараллельном движении равна
TSk3 = 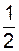 ·m3·(VC3)2 +
·m3·(VC3)2 + 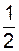 ·JC3X3·(ω3)2 =
·JC3X3·(ω3)2 =
= 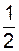 ·(0,3·m)·(0,166·V)2 +
·(0,3·m)·(0,166·V)2 + 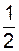 ·(m3·(i3X)2)·(1,666·V)2 =
·(m3·(i3X)2)·(1,666·V)2 =
= 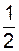 ·(0,3·m)·(0,166·V)2 +
·(0,3·m)·(0,166·V)2 + 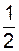 ·((0,3·m)·(0,18)2)·(1,666·V)2 = 0,03·m·V2.
·((0,3·m)·(0,18)2)·(1,666·V)2 = 0,03·m·V2.
Кинетическая энергия тела 4
TSk4 = 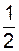 ·m4·(VC4)2 =
·m4·(VC4)2 = 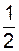 ·(1,5·m)·(0,166·V)2 = 0,02·m·V2.
·(1,5·m)·(0,166·V)2 = 0,02·m·V2.
Определим кинетическую энергию TSk механической системы:
TSk = 0,5·m·V2 + 0,147·m·V2 + 0,03·m·V2 + 0,02·m·V2 = 0,697 m·V2.
Таким образом, имеем TSk = 0,697 m·V2.
7. Показать внешние силы, действующие на точки механической системы при её движении (рис. 5.32).

Согласно рис. 5.32 на механическую систему действуют активные силы (G1, G2, G3, G4) и реакции (N1, F1, ZC2, YC2, TL) внешних связей, которые наложены на эту систему.
По условию задания сила F1 трения скольжения тела 1 при его движении по шероховатой поверхности связана с нормальной реакцией N1 соотношением F1 = f·N1, где f – коэффициент трения скольжения, N1 – модуль нормальной реакции N1.
Для определения модуля N1 реакции N1 рассмотрим поступательное движение тела 1, приняв его за материальную точку, в системе отсчёта O1X1Y1, происходящее под действием силы тяжести G1, нормальной реакции N1, силы трения F1 и реакции TА растянутой нити (рис. 5.33).
 |
Основное уравнение динамики для поступательно движущегося груза 1 имеет вид
m·aC1 = Σ  + Σ
+ Σ 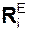 = G1 + N1 + F1 + TА,
= G1 + N1 + F1 + TА,
где aC1 – ускорение центра масс тела 1; TА – натяжение нити в точке А тела 1 (см. рис. 5.33).
Составим дифференциальное уравнение движения центра С1 масс груза 1, спроецировав последнее векторное равенство на координатную ось O1Y1.
m· 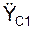 = Σ
= Σ  + Σ
+ Σ 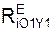 = – G1·cos(α) + N1.
= – G1·cos(α) + N1.
Поскольку проекция 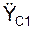 ускорения aC1 центра масс тела 1 на координатную ось O1Y1 равна нулю, то имеем
ускорения aC1 центра масс тела 1 на координатную ось O1Y1 равна нулю, то имеем
N1 = G1 ·cos(α) = m1·g·cos(α) = m·g·cos(α).
Тогда модуль силы трения находится по формуле
F1 = f·m·g·cos(α).
8. Определить перемещения SCi центров Ci масс тел механической системы в зависимости от перемещения SC1 центра С1 масс тела 1.
При решении рассматриваемого варианта курсового задания были определены зависимости, связывающие модуль скорости VC1 = V центра С1 масс тела 1 с модулями скоростей VC3, VC4 центров С3, С4 масс тел 3, 4.
VC3 = VC4 = 0,166·V.
Интегрируя эти выражения, получим
SC3 = SC4 = 0,166·SC1.
9. Определить сумму работ (Σ 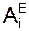 ) внешних сил, приложенных к механической системе, при перемещении центра С1 масс тела 1 на расстояние SC1.
) внешних сил, приложенных к механической системе, при перемещении центра С1 масс тела 1 на расстояние SC1.
Σ 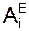 = Σ A(FiE) + Σ A(RiE),
= Σ A(FiE) + Σ A(RiE),
где ΣA(FiE) – сумма работ активных сил FiE на конечном перемещении механической системы; ΣA(RiE) – сумма работ реакций RiE внешних связей, наложенных на механичекую систему.
Сумму работ активных сил определим по формуле
ΣA(FiE) = A(G1) + A(G2) + A(G3) + A(G4),
где A(Gi) – работа силы тяжести i-го тела механической системы.
Согласно теоретическому материалу, изложенному в подразделе 5.5.1 данного учебно-методического пособия, справедливы следующие равенства:
A(G1) = G1·HC1 = m1·g·(SC1)·sin(α) =
= m·g·(SC1)·sin(α) = m·g·2·0,5 = m·g,
где HC1 – перемещение центра С1 масс тела 1 по высоте.
Работа A(G2) силы тяжести тела 2 равна нулю (A(G2) = 0), так как при движении механической системы центр масс С2 не изменяет своего положения.
Работу A(G3) силы тяжести G3 тела 3 определим по формуле
A(G3) = – G3·HC3 = – m3·g·SC3 = – 0,3·m·g·0,166·SC1 =
= – 0,3·m·g·0,166·2 = – 0,099 m·g,
где HC3 – перемещение центра С3 масс тела 3 по высоте.
Работа A(G4) силы тяжести G4 равна
A(G4) = – G4·HC4 = – m4·g·SC4 = – 1,5·m·g·0,166·SC1 =
= – 1,5·m·g·0,166·2 = – 0,5·m·g,
где HC4 – изменение положения центра С4 масс тела 4 по высоте.
Сумму работ ΣA(RiE) реакций RiE внешних связей определим по формуле
ΣA(RiE) = A(N1) + A(F1) + A(YC2) + A(ZC2) + A(TL),
где A(N1), A(F1), A(YC2), A(ZC2), A(TL) – работа соответствующей реакции внешней связи.
Работа A(N1) нормальной реакции N1 равна нулю (A(N1)=0), так как направление реакции N1 перпендикулярно направлению вектора SC1 перемещения точки её приложения.
Работа A(F1) силы трения F1 определяется по формуле
A(F1) = F1·SC1 = – F1·S = – (f·m·g·cos(α))·SC1 =
= – 0,12·m·g·0,866·2·= – 0,207·m·g.
Работы A(YC2), A(ZC2) реакций YC2, ZC2 шарнирно-неподвижной опоры в точке С2 соответственно равны нулю: (A(YC2) = 0; A(ZC2) = 0), так как при вращении тела 2 точки приложения реакций YC2, ZC2 не изменяют своего положения (SC2 = 0).
Работа A(TL) реакции TL растянутой нити равна нулю (A(TL)= 0), так как точка L приложения этой реакции не изменяет своего положения при движении механической системы.
Вычислим сумму работ Σ 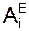 внешних сил, приложенных к механической системе, при перемещении центра С1 масс тела 1 на расстояние SC1.
внешних сил, приложенных к механической системе, при перемещении центра С1 масс тела 1 на расстояние SC1.
Σ 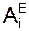 = ΣA(FiE) + ΣA(RiE) =
= ΣA(FiE) + ΣA(RiE) =
= m·g – 0,099·m·g – 0,5·m·g – 0,207·m·g = 0,194·m·g.
10. Определим скорость центра масс тела 1 в тот момент времени, когда пройденный им путь станет равным SC1.
TSk = 0,697·m·V2 = Σ 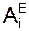 = 0,194·m·g.
= 0,194·m·g.
Решая последнее выражение, получим
V = 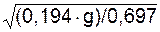 =
= 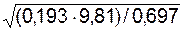 = 1,652 м/с.
= 1,652 м/с.
Таким образом, ответ на вопрос, поставленный в курсовом задании, получен:
VC1 = V = 1,652 м/с.
Вопросы и задания для самоконтроля
1. Сформулировать определение понятия «работа постоянной силы на прямолинейном перемещении точки её приложения».
2. Сформулировать определение понятия «элементарная работа переменной силы».
3. Записать формулу для определения работы силы тяжести.
4. Сформулировать определение понятия «мощность силы».
5. Сформулировать определение понятия «кинетическая энергия».
6. Записать формулу для определения кинетической энергии материальной точки.
7. Записать формулу для определения кинетической энергии поступательно движущегося твёрдого тела.
8. Записать формулу для определения кинетической энергии вращающегося тела относительно вертикальной оси.
9. Записать формулу для определения кинетической энергии для твёрдого тела, совершающего плоскопараллельное движение.
10. Записать формулу для определения кинетической энергии механической системы.
11. Записать формулу, выражающую теорему об изменении кинетической энергии неизменяемой механической системы.
Дата добавления: 2015-05-30; просмотров: 3221;
