Перемещения тел и точек механической системы

Перемещения точек механической системы не могут быть независимыми, так как на них наложены внешние и внутренние связи. Положение точек механической системы определяется только заданием независимых координат. Такие координаты называют обобщёнными координатами.

Обобщённые координаты механической системы – независимые между собой параметры, однозначно определяющие положение механической системы.

Число независимых координат равно числу степеней свободы механической системы. Так, например, для материальной точки, перемещающейся в пространстве, обобщёнными координатами (X = f₁(t), Y = f₂(t), Z = f₃(t)) являются уравнения движения точки. Точка в пространстве имеет три степени свободы. Для тела, совершающего вращательное движение, обобщённой координатой является зависимость φ = f(t) – угловой путь тела. Для плоскопараллельного движения твёрдого тела число обобщённых координат равно трём: X_C = f₁(t); Y_C = f₂(t); φ = f₃(t), где X_C, Y_C – координаты центра масс тела: φ – угол поворота тела относительно оси, проходящей через его центр масс.

Координаты любой точки механической системы являются функциями обобщённых координат (рис. 6.1).

Положение всех точек кривошипно-ползунного механизма вполне определяется заданием только угла поворота φ кривошипа. Этот угол и примем за обобщённую координату механизма. Таким образом, рассматриваемый механизм имеет одну степень свободы. Покажем, что координата точки В ползуна зависит от обобщённой координаты.

Х_B = OK + КB = r·cos(φ) + .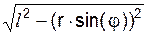

Нетрудно показать, что и координаты других точек (А, С) также зависят от обобщённой координаты φ:

Возможное (виртуальное) перемещение точки – любое допускаемое наложенными связями перемещение материальной точки из положения, занимаемого ею в данный момент времени, в бесконечно близкое положение, которое она может занимать в тот же момент времени.

Другими словами, возможные (или виртуальные) перемещения механической системы – воображаемые бесконечно малые перемещения, допускаемые в данный момент времени наложенными на систему связями.

Для иллюстрации этого понятия рассмотрим рычаг АВ, который может совершать вращательное движение (рис. 6.2).

Рычаг АВ рассматривается как механическая система, на которую наложена связь – шарнирно-неподвижная опора. В качестве обобщённой координаты используем угол φ поворота тела. Зададим углу φ бесконечно малое перемещение δφ, которое называют возможным угловым перемещением или приращением угловой координаты φ. При повороте рычага на угол δφ точки А и В переместятся по дугам АА^I, ВВ^I.

Возможные перемещения точек А и В рассматривают как величины первого порядка малости, поэтому криволинейные перемещения точек замещают направленными прямолинейными отрезками (векторами δS_A, δS_B), отложенными по касательным к траекториям точек. Модули возможных перемещений δS_A, δS_B точек А и В определяют по формулам:

δS_A = АО·δφ; δS_В = ВО·δφ.

Размерность возможных перемещений определяется размерностью обобщённой координаты: δφ [рад]; δS_A, δS_В [м]. Направления возможных перемещений точек механической системы совпадает с направлениями скоростей V_A, V_B этих точек.

В данном учебно-методическом пособии рассматриваются неизменяемые механические системы с одной степенью свободы. Материальные тела, входящие в такие механические системы, совершают следующие виды движений: поступательное, вращательное, плоскопараллельное. Рассмотрим подробнее эти движения.

Поступательное движение (рис. 6.3).

При поступательном движении возможные перемещения всех точек тела геометрически равны:

δS_A = δS_B = δS_С.

Так как тело при поступательном движении не поворачивается, то его возможное угловое перемещение равно нулю (δφ =0).

δS_A = V_A·δt; δS_B= V_B·δt; δS_C= V_C·δt,

где δt – бесконечно малый промежуток времени.

Вращательное движение (рис. 6.4).

За обобщённую координату в таком движении принимают угол поворота φ, а за возможное перемещение δφ – приращение угла поворота. Модули возможных перемещений δS_A, δS_A, δS_С точек А, В, С определяют по формулам:

δS_A = АО·δφ; δS_В= ВО·δφ; δS_С= СО·δφ.

Следует отметить, что при вращательном движении твёрдого тела возможные перемещения точек тела геометрически различны:

δS_A ≠ δS_A ≠ δS_С.

Согласно определению при плоскопараллельном движении тело имеет три степени свободы и, следовательно, этому соответствует три обобщённые координаты Х_С, Y_C, φ, где X_C, Y_C – координаты центра масс; φ – угол поворота тела относительно оси CZ₁, проходящей через его центр масс.

Из курса кинематики известно, что плоскопараллельное движение твёрдого тела можно представить как вращательное движение относительно оси, проходящей через мгновенный центр скоростей (МЦС). В этом случае в качестве обобщённой координаты используют только угол поворота φ.

Как правило, в инженерной практике возможные перемещения точек механической системы определяют с помощью мгновенного центра вращения (мгновенного центра поворота), положение которого всегда совпадает с положением мгновенного центра скоростей.

Мгновенный центр вращения – точка неподвижной плоскости, поворотом вокруг которой плоская фигура перемещается из данного положения в положение, бесконечно близкое к данному.

Рассмотрим частные случаи определения возможных перемещений точек тела при его плоскопараллельном движении.

Случай 1 (рис. 6.6).

Положение мгновенного центра вращения (точка Р) определяют так же, как и положение МЦС. Так как методика определения положения МЦС подробно рассмотрена в курсе кинематики, то здесь она не приводится. Модули возможных перемещений δS_A, δS_A, δS_С точек А, В, С определяют по формулам:

δS_A = АР·δφ;

δS_В = ВР·δφ;

δS_С = СР·δφ,

где АР, ВР, СР – соответственно расстояния от точек А, В, С до мгновенного центра вращения.

Необходимо еще раз напомнить, что возможные перемещения δS_A, δS_A, δS_С точек А, В, С связаны с их скоростями V_A, V_B, V_C следующими соотношениями:

δS_A = V_A·δt;

δS_B= V_B·δt;

δS_C= V_C·δt.

Таким образом, направления возможных перемещений точек и их скоростей совпадают.

Случаи 2, 3, 4 (рис. 6.7).

Формулы для определения модулей возможных перемещений точек А, В, С в случаях 2, 3, 4 остаются такими же, как и формулы для случая 1 (см. рис. 6.6).

Рассмотрим частный случай плоскопараллельного движения – мгновенно поступательное движение (рис. 6.8).

Из курса кинематики известно, что при мгновенно поступательном движении скорости всех точек тела геометрически равны:

V_A = V_B = V_C.

Так как δS_A = V_A·δt; δS_B = V_B·δt; δS_C = V_C·δt, то отсюда следует, что равны и возможные перемещения этих точек:

δS_A = δS_B = δS_C.

Возможные перемещения δS_A, δS_B точек А и В тела при его плоскопараллельном движении связаны соотношением

δS_A·cos(α) = δS_B·cos(β).

При решении задач аналитической механики все возможные перемещения точек механической системы выражают через приращение обобщённой координаты рассматриваемого механизма (рис. 6.10).

Согласно рис. 6.10 механическая система (кривошипно-ползунный механизм) состоит из трёх звеньев: 1 – кривошип; 2 – шатун; 3 – ползун. Механизм имеет одну степень свободы. В качестве обобщённой координаты используем угол φ₁ поворота тела 1. В заданном положении механизма обобщённой координате φ₁ зададим приращение δφ₁. Таким образом, δφ₁ – возможное угловое перемещение звена 1, которое совершает вращательное движение. Исходя из этого, определим модуль возможного перемещения δS_A.

δS_A = AO·δφ₁.

Кинематический анализ работы механизма показывает, что звено 2 совершает плоскопараллельное движение, а звено 3 совершает поступательное движение вдоль координатной оси ОХ. Из условия принадлежности точки В звену 3 возможное перемещение δS_В направлено вдоль координатной оси ОХ. Спроецировав возможные перемещения точек А и В на прямую, соединяющую эти точки, получим

δS_A = δS_В·cos(30^о).

Отсюда имеем

δS_В = δS_А/cos(30^о) = AO·δφ₁/cos(30^о).

Таким образом, установлено, что линейные возможные перемещения точек А и В зависят от возможного углового перемещения δφ₁ звена 1 механизма.

δS_A = AO·δφ₁ = f₁(δφ₁);

δS_B = AO·δφ₁/cos(30^о) = f₂(δφ₁).