Принцип возможных перемещений

При решении задач на равновесие механических систем, например, для составной конструкции применяются соответствующие уравнения равновесия. Как правило, такие задачи являются статически неопределимыми. Для их решения требуется рассматривать равновесие каждого из тел системы под действием активных сил, реакций внешних связей и реакций внутренних связей. В результате того, что для каждого из тел системы составляются уравнения равновесия, приходится решать большие системы уравнений. Такой подход к решению задачи становится громоздким и потому малопригодным. В этих случаях целесообразно использовать принцип возможных перемещений, который существенно облегчает решение поставленной задачи.

Формулировкапринципа возможных перемещений.

Для равновесия механической системы, на которую наложены стационарные идеальные связи, необходимо и достаточно, чтобы сумма работ активных (задаваемых) сил на любых возможных перемещениях механической системы равнялась нулю.

Этот принцип выражается формулой

δA = ΣδA(F_i) = ΣF_i·δS_i = ΣF_i·δS_i·cos(F_i, δS_i) = 0,

где F_i – активная сила, приложенная к i-й точке механической системы; δS_i – возможное перемещение точки приложения силы F_i.

Принцип возможных перемещений в декартовой системе отсчёта имеет вид

Σ(F_iOX·δS_iOX + F_iOY·δS_iOY + F_iOZ·δS_iOZ) = 0,

где F_iOX, F_iOY, F_iOZ – проекции задаваемых (активных) сил на координатные оси; δS_iOX, δS_iOY, δS_iOZ – проекции возможных перемещений δS_i точки приложения сил F_i на координатные оси.

Если предыдущую формулу (ΣF_i·δS_i = ΣF_i·δS_i·cos(F_i, δS_i) = 0) продифференцировать по времени, то получим

ΣF_i·V_i = ΣF_i·V_i·cos(F_i, V_i) = 0,

где V_i = d(δS_i)/dt – возможная скорость точки приложения силы F_i.

Так как по определению F·V = F·V·cos(F, V) = N, где N – мощность, то последнее равенство трактуют как принцип возможных скоростей или принцип возможных мощностей.

Для равновесия механической системы, на которую наложены стационарные идеальные связи, необходимо и достаточно, чтобы сумма мощностей активных сил на любых возможных скоростях точек этой системы равнялась нулю.

Для закрепления изложенного теоретического материала рекомендуется выполнить курсовые задания Д 6, Д7.

6.3.1. Варианты курсового задания Д 6

«Применение принципа возможных перемещений

к решению задач о равновесии сил, приложенных

к механической системе с одной степенью свободы»

Схемы механизмов, находящихся под действием взаимно уравновешивающихся сил, и необходимые для расчёта данные приведены в табл. 5.4. В расчётах использовать следующие условные обозначения: с – коэффициент жёсткости пружины (Н/см); h – деформация пружины (см); Q, P – силы (Н); М – момент пары сил (Н·м).

Примечания:

Вариант 6. Вес рукоятки О₁А не учитывать.

Вариант 7. Пружина сжата.

Вариант 8. Пружина сжата.

Вариант 10. Вес рукоятки ОА не учитывать.

Вариант 14. Вес стержней ОА и ОВ не учитывать; пружина растянута.

Вариант 16. Вес стержней О₁А и О₂В не учитывать.

Вариант 18. Р – вес блока радиуса R₃.

Вариант 19. Вес звена АВ не учитывать.

Вариант 24. Пружина сжата.

Вариант 25. Вес стержней АО и ВО не учитывать. Пружина растянута.

Вариант 26. Пружина растянута.

Применяя принцип возможных перемещений и пренебрегая силами сопротивления, определить величину, указанную в последнем столбце табл. 5.4.

Таблица 5.4

Номер варианта	Расчётная схема механизма	Исходные данные, определяемая величина
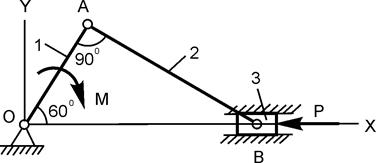
		ОА = 10 см; М = 20 Н·м; P = ?
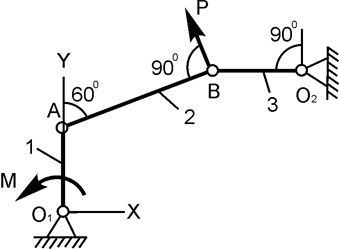
		О1А = 20 см; Р = 100 Н; M = ?
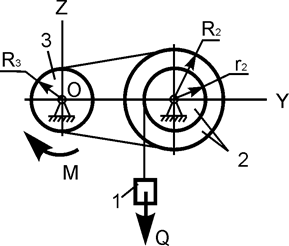
		R2 = 40 см; r2 = 30 см; R3 = 20 см; M = 100 Н·м; Q = ?

Продолжение табл. 5.4

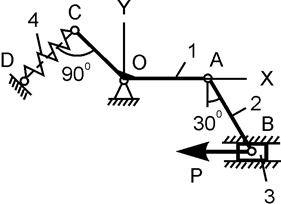
		ОС/ОА = 4/5; Р = 200 Н; h = 4 см; с = ?
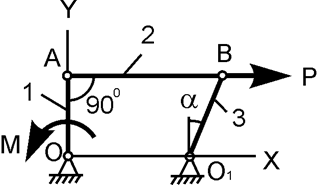
		ОА = 100 см; М = 10 Н·м; P = ?
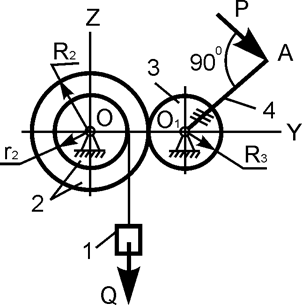
		R2 = 50 см; r2 = 15 см; R3 = 20 см; О1А = 80 см; Q = 200 H; P = ?

Продолжение табл. 5.4

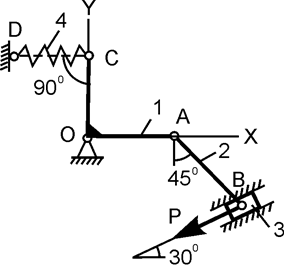
		OC = OA; с = 10 Н/см; h = 3 см; P = ?
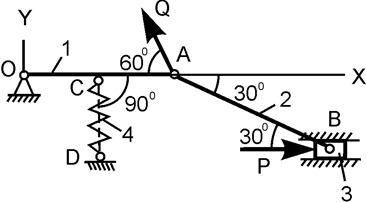
		ОС = АС; Р = 200 Н; с = 10 Н/см; h = 2 см; Q = ?
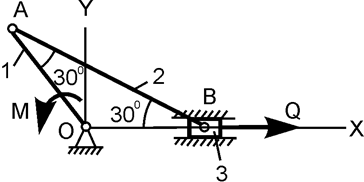
		ОА = 20 см; Q = 200 H; M = ?

Продолжение табл. 5.4

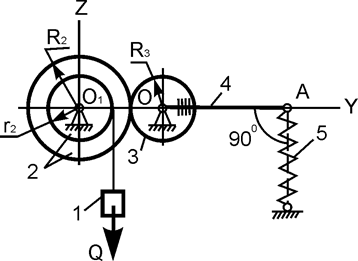
		R2 = 40 см; r2 = 15 см; R3 = 20 см; ОА = 100 см; Q = 2000 H; h = 4 см; с = ?
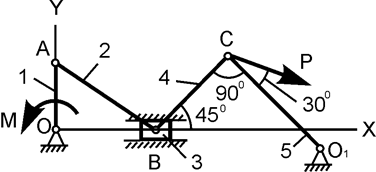
		ОА = 20 см; М = 300 Н·м; P = ?
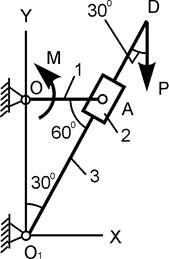
		O1D = 60 см; АО = 20 см; М = 100 Н·м; P = ?

Продолжение табл. 5.4

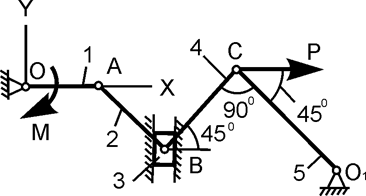
		ОА = 40 см; М = 200 Н·м; P =?
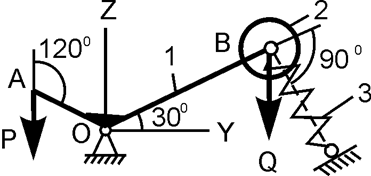
		ОВ = 2ОА; Q = 20 H; с = 25 Н/см; h = 3 см; P = ?
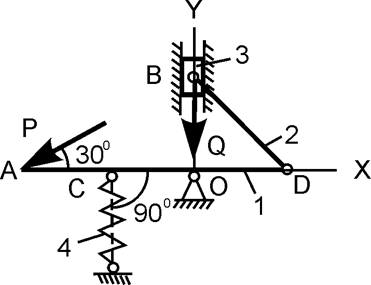
		АС = ОС = ОD; Q = 3000 H; с = 250 Н/см; h = 3 см; P = ?

Продолжение табл. 5.4

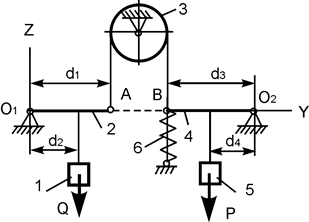
		d1 = 100 см; d2 = 60 см; d3 = 80 см; d4 = 40 см; Q = 5000 H; c = 100 Н/см; h = 4 см; P = ?
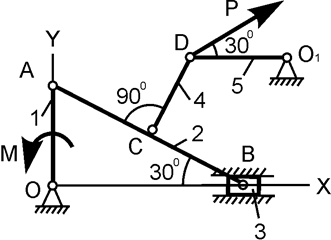
		ОА = 20 см; М = 200 Н·м; P = ?
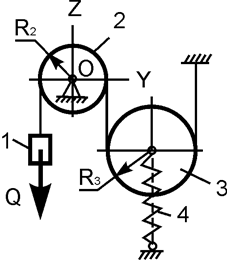
		Q = 200 H; P = 200 H; с = 100 H/см; h = ?

Продолжение табл. 5.4

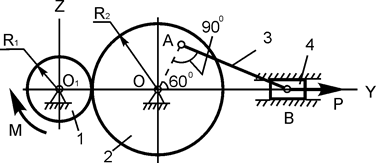
		R1 = 20 см; R2 = 30 см; ОА = 25 см; М = 100 Н·м; P = ?
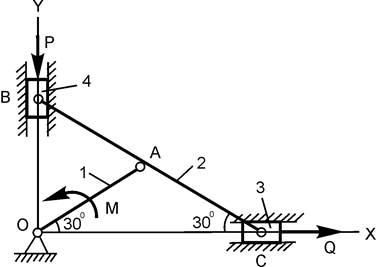
		ОА=АВ =50 см; АС = 50 см; Q = 50 H; P = 100 H; M = ?
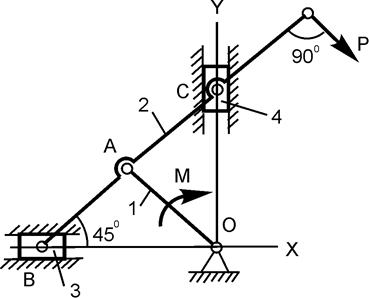
		ОА=АВ= 25 см; АС=DC= 25 см; Р = 200 Н; M = ?

Продолжение табл. 5.4

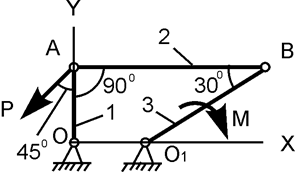
		ОА = 40 см; М = 400 Н/см; P = ?
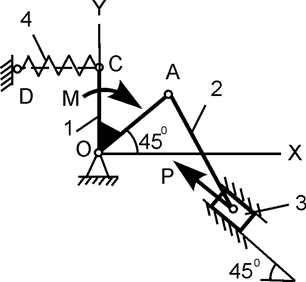
		ОС =2ОА = 1 м; Р = 200 Н; М = 50 Н·м; с = 50 Н/см; h = ?
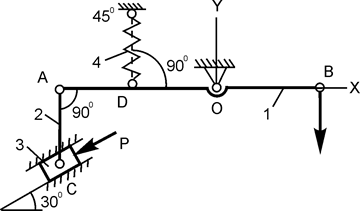
	Q	AD = OD = OB; P = 250 H; c = 150 H/см; h = 2,5 см; Q = ?

Продолжение табл. 5.4

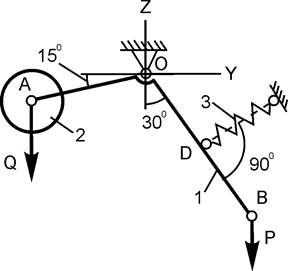
		OD=DB=0,8AO; Q = 400 H; c = 120 H/см; h = 3 см; P = ?
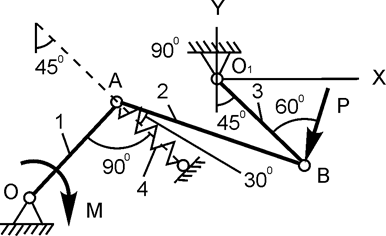
		ОА = 25 см; Р = 500 Н; М = 120 Н·м; h = 2 см; с = ?
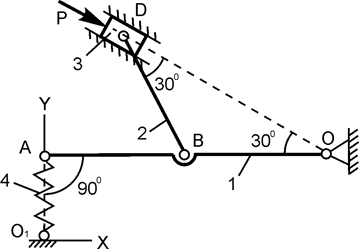
		ОВ = АВ; c = 180 Н/см; h = 2 см; P = ?

Окончание табл. 5.3

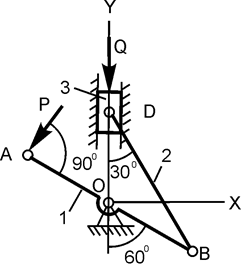
		ОВ = (5/4)ОА; Р = 450 Н; Q = ?
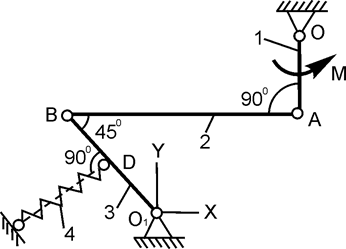
		AO = 30 см; BD = O1D; M = 120 H·м; с = 100 Н/см; h = ?
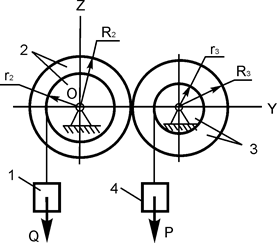
		R2 = 36 см; r2 = 15 см; R3 = 20 см; r3 = 10 см; Р = 600 Н; Q =?

6.3.2. Пример выполнения курсового задания Д 6

При выполнении курсовых заданий Д 6, Д 7 необходимо учесть следующие замечания.

1. Если не все связи, наложенные на рассматриваемую механическую систему, являются идеальными, например, имеются шероховатые поверхности (неидеальные связи), то к активным нагрузкам следует добавить силы трения. Таким приёмом силы трения переносят в разряд активных сил и, следовательно, шероховатую поверхность можно рассматривать как идеальную связь (рис. 6.14).

Таким образом, при решении задачи рис. 6.14,а и рис. 6.14,б эквивалентны.

2. Если требуется определить какую-либо реакцию идеальной связи, то, применив аксиому связей, отбрасывают соответствующую связь и заменяют её реакцией связи. Таким образом, исходная связь заменяется другой связью, допускающей возможные перемещения. Тем самым искомая реакция переносится в разряд активных сил. Этот приём решения задач является черезвычайно эффективным, так как искомая реакция связи непосредственно определяется из уравнения, выражающего принцип возможных перемещений.

В исходном положении (см. рис. 6.15) на механическую систему, состоящую из двух тел, в точке А наложена связь – жёсткая заделка. Снимем ограничение на перемещение тела 1 в горизонтальном направлении, сохранив остальные ограничения. Варианты такой замены показаны на рис. 6.15,б, 6.15,в.

При таких заменах тело 1 может совершить только поступательное движение, параллельное координатной оси ОХ. Если задать возможное перемещение δS_A точке А механической системы, то её точки В и С получат возможные перемещения δS_В, δS_С, зависящие от δS_A.

При определении реактивного момента М_А для механической системы, приведённой на рис 6.15, жёсткую заделку заменяют шарнирно-неподвижной опорой (см. рис. 6.16).

При такой замене тело 1 может совершать вращательное движение. Зададим этому телу возможное угловое перемещение δφ₁. Точки В и С механической системы получат линейные возможные перемещения δS_В, δS_С, зависящие от перемещения δφ₁.