Общее уравнение динамики

6.4.1. Общее уравнение динамики механической системы

Принцип возможных перемещений, дающий общий метод решения задач статики, можно применить и к решению задач динамики, если его дополнить принципом Даламбера.

Рассмотрим движение несвободной неизменяемой механической системы, на которую наложены идеальные связи, в инерциальной системе отсчёта OXYZ (рис. 6.25).

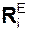Согласно принципу Даламбера i-я точка механической системы совершает движение под действием активной силы , реакции внешней связи, реакции 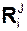внутренней связи и силы инерции Ф_i. Этот принцип выражается формулой

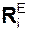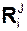+ + + Ф_i = 0.

Пусть точка С_i механической системы получит возможное перемещение δS_С_i. Очевидно, что элементарная работа δА сил, приложенных к точке, равна нулю.

δА = ( + + 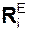+ 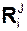Ф_i)·δS_С_i = 0.

Просуммируем последние выражения и получим

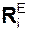Σ ·δS_С_i +Σ ·δS_С_i + Σ 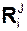·δS_С_i + ΣФ_i·δS_С_i = 0.

Для движущейся механической системы сумма работ активных сил, реакций внешних связей, внутренних сил и сил инерции, приложенных к её точкам, на любых возможных перемещениях этой системы равна нулю.

Поскольку на механическую систему наложены идеальные связи, то сумма работ реакций этих связей равна нулю.

Σ 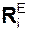·δS_С_i = 0.

Так как рассматривается неизменяемая механическая система, то сумма работ реакций внутренних связей также равна нулю.

Σ 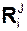·δS_С_i = 0.

Исходя из того, что Σ 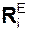·δS_С_i = 0 и Σ 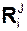·δS_С_i = 0, получим

Σ ·δS_С_i + ΣФ_i·δS_С_i = 0.

Последнее уравнение называют общим уравнением динамики.

В любой момент времени работа активных сил и сил инерции материальных точек несвободной механической системы с идеальными связями на её любом возможном перемещении равна нулю.

Общее уравнение динамики (Σ ·δS_С_i + ΣФ_i·δS_С_i = 0) можно преобразовать к следующим видам:

Σ( + Ф_i)·δS_С_i = 0;

Σ 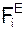·δS_С_i·cos( , δS_С_i) + ΣФ_i·δS_С_i·cos(Ф_i, δS_С_i) = 0;

Σ( ·δS_i_ОХ + ·δS_iOY + ·δS_iOZ) +

+ Σ(Ф_iOX·δS_iOX + Ф_iOY·δS_iOY + Ф_iOZ·δS_iOZ) = 0;

Σ( ·δS_iOX + ·δS_iOY + ·δS_iOZ) +

+ Σ(– m· 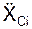·δS_iOX – m· 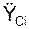·δS_iOY – m· 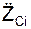·δS_iOZ) = 0,

где , , – проекции активных сил на координатные оси; Ф_iOX, Ф_iOY, Ф_iOZ – проекции сил инерции на координатные оси; δS_iOX, δS_iOY, δS_iOZ – проекции возможных перемещений точек приложения сил на координатные оси, 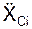, , 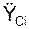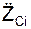– проекции ускорений материальных точек механической системы на координатные оси.

Общее уравнение динамики позволяет составить дифференциальные уравнения движения любой механической системы.

Если среди связей системы имеются односторонние связи, то для применения общего уравнения динамики необходимо, чтобы возможные перемещения системы не разрушали эти связи, а обеспечивали их функциональное назначение.

Для закрепления изложенного теоретического материала рекомендуется выполнить курсовое задание Д 8.

6.4.2. Варианты курсового задания Д 8

«Применение общего уравнения

динамики к исследованию движения механической

системы с одной степенью свободы»

Для заданной механической системы определить ускорения центров масс грузов 1. Массами нитей пренебречь. Трение качения и силы сопротивления в подшипниках не учитывать. Система движется из состояния покоя.

Варианты механических систем и необходимые для решения данные приведены в табл. 5.6.

Блоки и катки, для которых радиусы инерции в табл. 5.6 не указаны, считать сплошными однородными цилиндрами.

Примечания:

Радиусы инерции даны относительно центральных осей, перпендикулярных плоскости чертежа.

Коэффициенты трения принимать одинаковыми при скольжении тел по плоскостям.

Таблица 5.6

Номер варианта	Расчётная схема механизма	Исходные данные

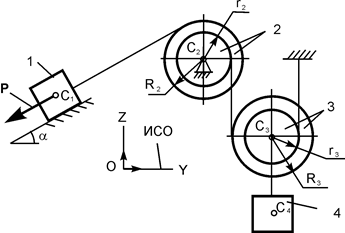
		P = 10G; G₁ = G; G₂ = 2G; G₃ = 3G; G₄ = 4G; r₂ = r; R₂ = 2r; r₃ = r; R₃ = 2r; i_C2X2 = r ; i_C3X3 = r ; a = 30^о; f = 0,1
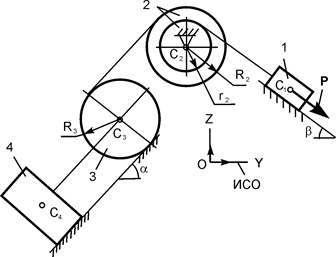
		P = 10G; G₁ = G; G₂ = 2G; G₃ = 3G; G₄ = 4G; R₂ = r; R₃ = 2r; a = 45^о; b = 45^о; f = 0,1
		P = 10G; G₁ = G; G₂ = 2G; G₃ = 3G; G₄ = 4G; r₂ = r; R₂ = 2r; R₄ = r; i_C2X2 = r ; a = 30^о; f = 0,1

Продолжение табл. 5.6


		P = 10G; G₁ = G; G₂ = 2G; G₃ = 3G; G₄ = 4G; r₂ = r; R₂ = 2r; R₃ = r; R₄ = r; i_C₂_X₂ = r ; a = 30^о
		P = 10G; G₁ = G; G₂ = 2G; G₃ = 3G; G₄ = 4G; r₂ = r; R₂ = 2r; r₃ = r; R₃ = 2r; i_C2X2 = r ; i_C3X3 = r ; f = 0,1
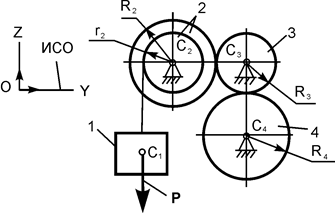
		P = 10G; G₁ = G; G₂ = 2G; G₃ = 3G; G₄ = 4G; r₂ = r; R₂ = 2r; R₃ = r; R₄ = 2r; i_C2X2 = r

Продолжение табл. 5.6


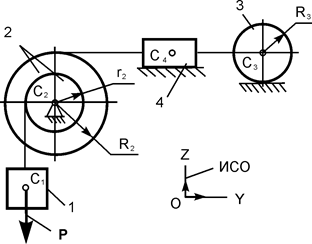
		P = 10G; G₁ = G; G₂ = 2G; G₃ = 3G; G₄ = 4G; r₂ = r; R₂ = 2r; R₃ = r; i_C₂_X₂ = r ; f = 0,1
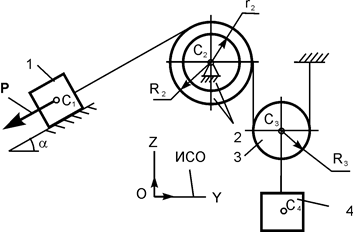
		P = 10G; G₁ = G; G₂ = 2G; G₃ = 3G; G₄ = 4G; r₂ = r; R₂ = 2r; R₃ = r; i_C2X2 = r ; a = 30^о; f = 0,1
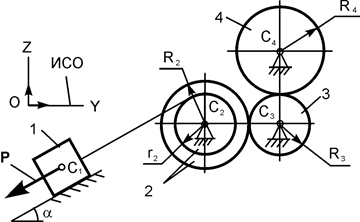
		P = 10G; G₁ = G; G₂ = 2G; G₃ = 3G; G₄ = 4G; r₂ = r; R₂ = 2r; R₃ = r; R₄ = 2r; i_C2X2 = r ; a = 30^о; f = 0,1

Продолжение табл. 5.6


		P = 10G; G₁ = G; G₂ = 2G; G₃ = 3G; G₄ = 4G; r₂ = r; R₂ = 2r; R₃ = 2r; i_C2X2 = r ; a = 45^о; b = 45^о; f = 0,1
		P = 10G; G₁ = G; G₂ = 2G; G₃ = 3G; G₄ = 4G; r₂ = r; R₂ = 2r; R₃ = r; i_C2X2 = r ; a = 30^o; f = 0,1
		P = 10G; G₁ = G; G₂ = 2G; G₃ = 3G; G₄ = 4G; r₂ = r; R₂ = 2r; R₃ = r; i_C2X2 = r ; a = 30^о; f = 0,1

Продолжение табл. 5.6


		P = 10G; G₁ = G; G₂ = 2G; G₃ = 3G; G₄ = 4G; R₂ = 2r; R₃ = r; i_C₂_X₂ = r ; a = 30^о; f = 0,1
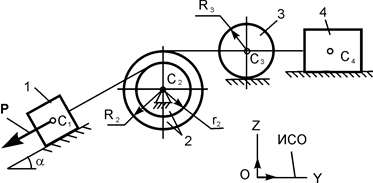
		P = 10G; G₁ = G; G₂ = 2G; G₃ = 3G; G₄ = 4G; r₂ = r; R₂ = 2r; R₃ = r; i_C2X2 = r ; a = 30^о; f = 0,1
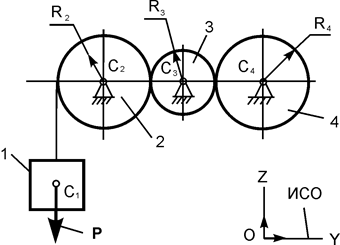
		P = 10G; G₁ = G; G₂ = 2G; G₃ = 3G; G₄ = 4G; R₂ = 2r; R₃ = r; R₄ = 2r

Продолжение табл. 5.6


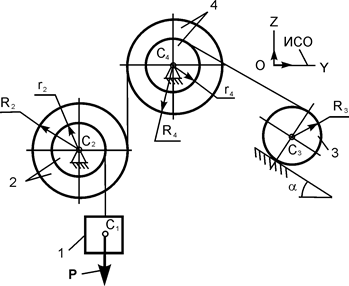
		P = 10G; G₁ = G; G₂ = 2G; G₃ = 3G; G₄ = 4G; r₂ = r; R₂ = 2r; R₃ = r; r₄ = r; R₄ = 2r; i_C2X2 = r ; i_C4X4 = r
		P = 10G; G₁ = G; G₂ = 2G; G₃ = 3G; G₄ = 4G; R₂ = r; R₃ = r
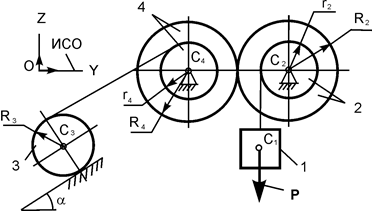
		P = 10G; G₁ = G; G₂ = 2G; G₃ = 3G; G₄ = 4G; r₂ = r; R₂ = 2r; R₃ = r; r₄ = r; R₄ = 2r; i_C2X2 = r ; i_C4X4 = r ; a = 30^о

Продолжение табл. 5.6


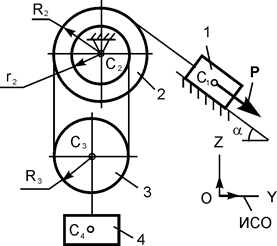
		P = 10G; G₁ = G; G₂ = 2G; G₃ = 3G; G₄ = 4G; r₂ = r; R₂ = 2r; R₃ = 1,5r; i_C2X2 = r ; a = 45^о; f = 0,1
		P = 10G; G₁ = G; G₂ = 2G; G₃ = 3G; G₄ = 4G; R₂ = r; r₃ = r; R₃ = 2r; i_C3X3 = r ; i_C4X4 = r ; a = 30^о; b = 45^о; f = 0,1
		P = 10G; G₁ = G; G₂ = 2G; G₃ = 3G; G₄ = 4G; R₂ = r; R₃ = r; a = 45^о; f = 0,1

Продолжение табл. 5.6


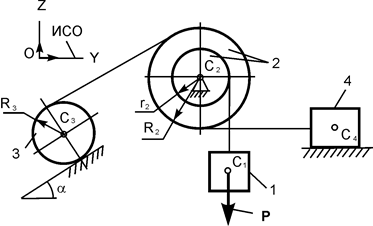
		P = 10G; G₁ = G; G₂ = 2G; G₃ = 3G; G₄ = 4G; r₂ = r; R₂ = 2r; R₃ = r; i_C2X2 = r ; a = 30^о; f = 0,1
		P = 10G; G₁ = G; G₂ = 2G; G₃ = 3G; G₄ = 4G; r₂ = r; R₂ = 2r; R₃ = 2r; i_C2X2 = r ; a = 45^о_; b = 45^о; f = 0,1
		P = 10G; G₁ = G; G₂ = 2G; G₃ = 3G; G₄ = 4G; r₂ = r; R₂ = 2r; R₃ = 2r; i_C2X2 = r ; a = 45^о; f = 0,1

Продолжение табл. 5.6


		P = 10G; G₁ = G; G₂ = 2G; G₃ = 3G; G₄ = 4G; R₂ = r; R₃ = r; a = 45^о_; b = ; f = 0,1
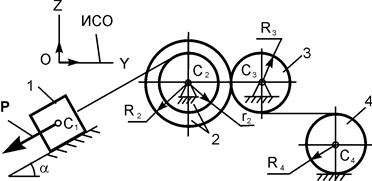
		P = 10G; G₁ = G; G₂ = 2G; G₃ = 3G; G₄ = 4G; r₂ = r; R₂ = 2r; R₃ = r; R₄ = r; i_C2X2 = r ; a = 30^о; f = 0,1
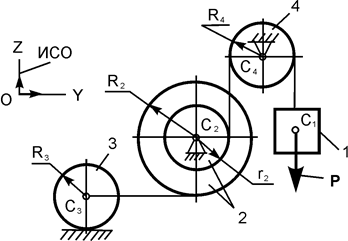
		P = 10G; G₁ = G; G₂ = 2G; G₃ = 3G; G₄ = 4G; r₂ = r; R₂ = 2r; R₃ = r; R₄ = r; i_C2X2 = r

Окончание табл. 5.6


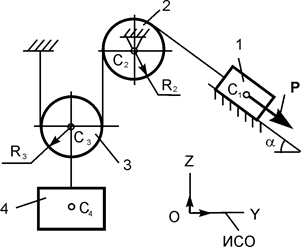
		P = 10G; G₁ = G; G₂ = 2G; G₃ = 3G; G₄ = 4G; R₂ = r; R₃ = r; a = 45^о; f = 0,1
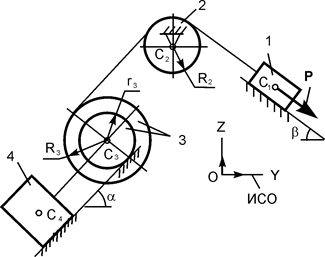
		P = 10G; G₁ = G; G₂ = 2G; G₃ = 3G; G₄ = 4G; R₂ = r; r₃ = r; R₃ = 2r; i_C3X3 = r ; a = 45^о; b = 45^о; f = 0,1
		P = 10G; G₁ = G; G₂ = 2G; G₃ = 3G; G₄ = 4G; R₂ = 2r; R₃ = r; a = 45^о; f = 0,1

6.4.3. Пример выполнения курсового задания Д 8

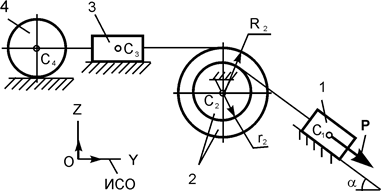
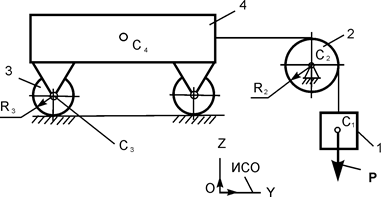
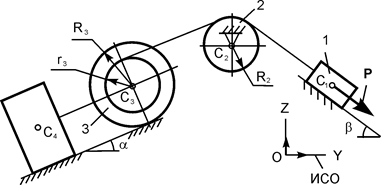
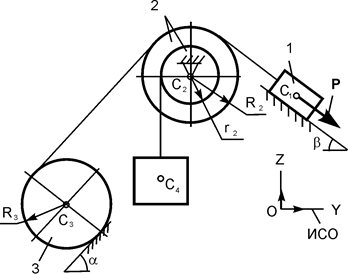
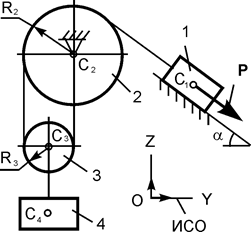
Для заданной механической системы (рис. 6.26) определить ускорение груза 1 при его опускании.

Дано: G₁ = 8G; G₂ = 4G; G₃ = 2G; P = G; f₃ = 0,1; i_C₂_X₂ = 0,1 м; f₄ = 0,1; α = 30^o; b = 0,5 м; d = 0,4 м; r₂ = 0,2 м; R₂ = 0,5 м, где G₁, G₂, G₃ – вес соответствующих тел механической системы; f₃ – коэффициент трения скольжения тела 3 при его движении по шероховатой поверхности; f₄ – коэффициент трения скольжения между телами 2 и 4; i_C₂_X₂ – радиус инерции тела 2 относительно оси, проходящей через его центр масс; α, b, d, r₂, R₂ – геометрические параметры. Механическая система начинает движение из состояния покоя.

Решение.

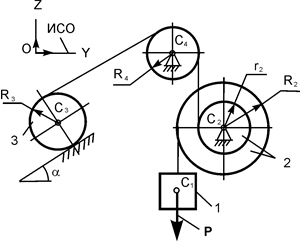
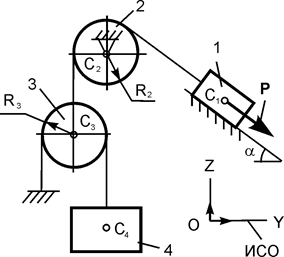
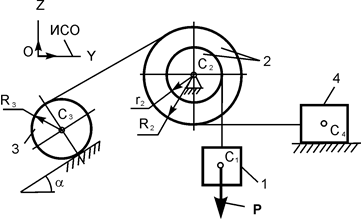
Рассмотрим движение механической системы, состоящей из тел 1, 2, 3 (рис. 6.27), предположив, что груз 1 опускается ускоренно.

Согласно общему уравнению динамики механическая система совершает движение под действием активных сил: G₁, G₂, G₃ – силы тяжести тел 1, 2, 3; F₃ – сила трения при движении груза 3 по шероховатой поверхности; F_4-2 – сила трения при скольжении цилиндрической поверхности тела 2 по тормозной колодке тела 4 и инерционных нагрузок: Ф₁, Ф₃ – силы инерции тел 1, 3; 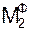– момент сил инерции при вращении тела 2 относительно оси С₂Х₂.

Как это отмечалось ранее, при наличии неидеальных связей, наложенных на механическую систему, эти связи необходимо преобразовать в идеальные путём переноса сил трения в разряд активных сил.

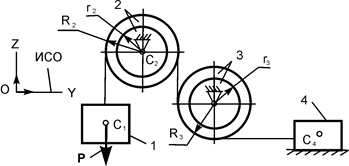
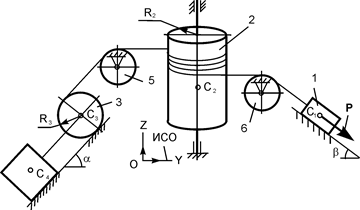
Для определения силы трения F_4-2 механическую систему, показанную на рис. 6.26, расчленим по внутренней связи и рассмотрим равновесие рычага 4 (рис. 6.28).

На тело 4 действуют: активная сила Р; реакции Y_A, Z_A внешней связи в точке А (шарнирно-неподвижная опора); реакции N_2-4, F_2-4 внутренней связи. Направления сил N_2-4, F_2-4 показывают, как тело 2 действует на тело 4. Составим уравнение равновесия.

ΣM_A( 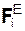) + ΣM_A( 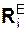) = N_2-4·b – P·(b + d) = 0.

Из этого уравнения определим модуль нормальной реакции

N_2-4 = P·(b + d)/b = G·(b + d)/b.

Согласно закону сухого трения (закону Кулона) сила трения F_2-4 связана с нормальной реакцией N_2-4 соотношением

F_2-4 = f₄·N_2-4 = f₄·G·(b + d)/b.

По известному закону динамики (закон равенства действия и противодействия) имеем

F_4-2 = F_2-4 = f₄·G·d/b.

Таким образом, сила F_4-2 трения, приложенная к телу 2 со стороны тела 4 (см. рис. 6.27), определена.

Для определения силы F₃ трения рассмотрим поступательное движение груза 3 (рис. 6.29) в инерциальной системе отсчёта O₃Y₃X₃. Используя известные положения динамики, примем груз 3 за материальную точку.

На рис. 6.29 использованы условные обозначения: N₃ – нормальная реакция шероховатой поверхности; V_С3, a_С3 – соответственно скорость и ускорение центра масс тела 3.

Составим дифференциальное уравнение поступательного движения тела 3.

m· 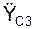= – G₃·cos(α) + N₃,

где 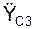– проекция ускорения a_С3 на координатную ось O₃Y₃.

Так как 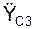= 0, то получим

N₃ = G₃·cos(α).

Тогда имеем

F₃ = f₃·N₃ = f₃·G₃·cos(α) = f₃·2·G·cos(α).

Таким образом, сила трения F₃ определена.

Вернёмся к рис. 6.27. Зададим возможное перемещение δS_С1 центру масс тела 1. При этом тело 2 получит возможное угловое перемещение δφ₂ = δS_С1/R₂, а центр С₃ масс тела 3 получит возможное линейное перемещение, модуль которого δS_С3 = δS_С1·(r₂/R₂). Двойным дифференцированием по времени возможных перемещений δφ₂, δS_С3 определим угловое ускорение 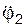тела 2 и модуль a_С3 ускорения центра масс тела 3.

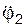= a_С₁/R₂; a_С₃ = a_С₁·(r₂/R₂).

К рассматриваемой механической системе приложим активные силы G₁, G₂, G₃, F₃, F_4-2 и инерционные нагрузки Ф₁, Ф₂, .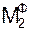

Модули сил инерции Ф₁, Ф₃ и момента 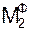сил инерции определяют по формулам:

Ф₁ = m₁·a_С1 = (G₁/g)·a_С1 = (8·G/g)·a_С1;

Ф₃ = m₁·a_С3 = (G₃/g)·a_С3 = (2·G/g)·a_С1·(r₂/R₂);

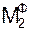= J_С2Х2· 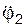= m₂·(i_С2Х2)²· 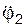= (G₂/g)·(i_С2Х2)²· =

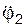= (4·G/g)·(i_С2Х2)²·(a_С1/R₂).

Запишем общее уравнение динамики для рассматриваемой механической системы:

Σ 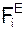·δS_С_i·cos( , δS_С_i) + ΣФ_i·δS_С_i·cos(Ф_i, δS_С_i) = 0.

Определим первое слагаемое правой части этого уравнения.

Σ 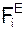·δS_С_i·cos( , δS_С_i) =

= G₁·δS_С1 – F_4-2·δS_С1 – G₃·δS_С3·sin(α) – F₃·δS_С3 =

= 8·G·δS_С1 – f₄·G·((b + d)/b)·δS_С1 – 2·G·δS_С1·(r₂/R₂)·sin(α) –

– f₃·2·G·cos(α)·δS_С₁·(r₂/R₂) =

= G·(8 – f₄·((b + d)/b) – 2·(r₂/R₂)·sin(α) – f₃·2·G·cos(α)·(r₂/R₂))·δS_С₁.

Определим второе слагаемое правой части общего уравнения динамики:

ΣФ_i·δS_С_i·cos(Ф_i, δS_Ci) = – Ф₁·δS_С1 – 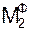·δφ₂ – Ф₃·δS_С3 =

= – (8·G/g)·a_С1·δS_С1 – (4·G/g)·(i_С2Х2)²·(a_С1/R₂)·(δS_С1/R₂) –

– (2·G/g)·a_С1·(r₂/R₂)·δS_С1·(r₂/R₂) =

= – (G/g)·(8 + 4·(i_С2Х2/R₂)² + 2·(r₂/R₂)²)·a_С1·δS_С1.

Внося эти слагаемые в общее уравнение динамики, получим

G·(8 – f₄·((b + d)/b) – 2·(r₂/R₂)·sin(α) – f₃·2·G·cos(α)·(r₂/R₂))·δS_С1 –

– (G/g)·(8 + 4·(i_С2Х2/R₂)² + 2·(r₂/R₂)²)·a_С1·δS_С1 = 0.

Отсюда определим модуль a_С1 ускорения центра масс груза 1:

a_C1 = g·(8 – f₄·((b + d)/b) – 2·(r₂/R₂)·sin(α) – f₃·2·cos(α)·(r₂/R₂))/

/(8 + 4·(i_С2Х2/R₂)² + 2·(r₂/R₂)²) =

= 9,81·(8 – 0,1·((0,5 + 0,4)/0,5) – 2·(0,2/0,5)·0,5 –

– 0,1·2·0,866·(0,2/0,5))/

/(8 + 4·(0,1/0,5)² + 2·(0,2/0,5)²) = 9,584 м/с².

Таким образом, ответ на вопрос (a_С1 =?), поставленный в курсовом задании Д 8, получен.

Вопросы и задания для самоконтроля

1. Записать формулу, выражающую общее уравнение динамики, в векторной форме.

2. Записать формулу, выражающую общее уравнение динамики, в скалярной форме.

3. Записать формулу, выражающую общее уравнение динамики, в координатной форме.

<49 50 515253 54 55 >

Дата добавления: 2015-05-30; просмотров: 2424;