Гироскопический момент
При изменении положения оси гироскопа (рис. 7.8) формируется гироскопический момент 
относительно точки О, который определяют по формуле
= JO1Z1· 
× 
,
где JO1Z1 – момент инерции гироскопа относительно оси O1Z1; – вектор угловой скорости вращения гироскопа относительно оси O1Z1; – вектор угловой скорости вращения гироскопа относительно оси прецессии OZ.
На рис. 7.8 оси OZ, O1Z1 расположены в плоскости OYZ. Согласно правилу векторного произведения вектор одновременно перпендикулярен векторам , и направлен в сторону, откуда виден поворот вектора к вектору , происходящий против хода часовой стрелки. Исходя из этого правила, вектор лежит на оси ОХ и направлен в сторону увеличения координаты Х. Модуль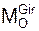 
гироскопического момента определяют по формуле
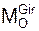= JO1Z1·I I·I I = JO1Z1·ω·ω1·sin(θ),
где ω = I I, ω1 = I I – модули векторов , ; θ – угол, составленный векторами , .
Гироскопический момент стремится совместить ось гироскопа с осью прецессии.
Рассмотрим быстрое вращение тела 1 с угловой скоростью 
в рамке 2, которая вращается относительно угловой оси OY с угловой скоростью 
(рис. 7.9).
При этом выполняется неравенство I I >> I I. По отношению к рамке 2 цилиндрические шарниры в точках А и В являются внешними связями. В этих связях формируются гироскопические (динамические) реакции RA, RB, противодействующие моменту . Реакции RA, RB образуют пару сил, алгебраический момент MSopr которой равен
MSopr = RA·h.
| |
Вектор MSopr этой пары сил направлен противоположно вектору
гироскопического момента (рис. 7.10).
Вектор MSopr момента реакций опор А и В и его модуль MSopr можно также определять по формулам:
MSopr = – = × JOХ· ·= – JOХ· × ;
MSopr = JOХ·ω·ω1·= – JOХ·I I×I I.
Задачи на определение гироскопических реакций опор рекомендуется решать по следующему алгоритму.
1. Изобразить на рисунке векторы угловой скорости собственного вращения гироскопа и его кинетического момента LO = JOХ· .
2. Определить и изобразить на рисунке вектор угловой скорости прецессии оси гироскопа.
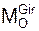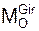3. Найти гироскопический момент и его модуль по формулам: = JO1Z1· × ; = JO1Z1·I I·I I = JO1Z1·ω·ω1·sin(θ),
где ω = I I, ω1 = I I – модули векторов , ; θ – угол, составленный векторами , .
4. Определить вектор MSopr момента реакций опор А и В и его модуль MSopr по формулам:
MSopr = – = × JOХ· ·= – JOХ· × ;
MSopr = JOХ·ω·ω1·= – JOХ·I I×I I.
5. Определить модуль реакции одной из опор гироскопа по формуле RA = JOХ·ω·ω1/h.
УДАР
Дата добавления: 2015-05-30; просмотров: 2323;