Удар шара о неподвижную плоскость
Рассмотрим удар поступательно движущегося шара о неподвижную плоскость (рис. 8.6).
Шар массой m движется поступательно и скорость VC направлена по нормали к неподвижной массивной поверхности в точке А. В момент времени, когда шар достигает этой поверхности, происходит прямой центральный удар. Различают две фазы этого удара. В течение первой фазы шар деформируется до тех пор, пока скорость его не станет равной нулю. Во время этой фазы кинетическая энергия шара обращается в потенциальную энергию сил упругости деформируемых тел и частично расходуется на их нагревание. В течение второй фазы под действием сил упругости шар частично восстанавливает свою первоначальную форму. Из-за остаточных деформаций и нагревания шара первоначальная кинетическая энергия шара полностью не восстанавливается. Поэтому шар отделяется от неподвижной поверхности с абсолютной скоростью UС, модуль которой меньше модуля его скорости VC до удара.
 |
Согласно рис. 8.6, шар падает на неподвижную горизонтальную плоскость с высоты h1, при этом начальная скорость его центра масс равна нулю (VC0 = 0). В начале процесса удара скорость его центра масс равна VC. В конце удара шар со скоростью центра масс UС отрывается от неподвижной поверхности и поднимается на высоту h2max, где скорость его центра масс равна нулю.
По известным величинам h1, h2max определяют коэффициент восстановления при ударе по формуле
k = 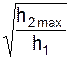 .
.
Эта формула используется при экспериментальном определении коэффициента восстановления.
В случае абсолютно неупругого удара шар от плоскости не отделяется, т е. h2 = 0. Тогда k = 0.
При абсолютно упругом ударе шар отскакивает от неподвижной плоскости и возвращается в исходное положение, т. е. h2max = h1. В этом случае k = 1.
При упругом ударе h2max < h1 и, следовательно, 0 < k < 1.
В случае прямого центрального удара тела о неподвижную поверхность модули скоростей связаны соотношением
UС = k·VC.
 |
Рассмотрим косой удар шара о неподвижную горизонтальную плоскость (рис. 8.7).
Шар ударяется о неподвижную плоскость со скоростью VC, которая направлена к этой плоскости под углом α. После удара шар отскакивает от неподвижной плоскости со скоростью UС, под углом β к плоскости. Коэффициент восстановления при ударе определяют по формуле
k = 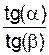 .
.
Последняя формула указывает удобный способ экспериментального определения коэффициента восстановления k при упругом ударе. По этому способу замеряют угол α и угол β отражения.
В случае абсолютно упругого удара угол падения α равен углу отражения β, откуда k = 1.
Задачи на определение коэффициента восстановления при ударе решают по следующему алгоритму.
1. Направить на рисунке главную нормаль (ось On) вдоль линии центров, а касательную (ось Оt) – перпендикулярно к ней.
2. Вычислить проекции скоростей VC1On, VC2On центров масс С1, С2 соударяющихся тел в начале удара на главную нормаль.
3. Вычислить проекции скоростей UC1On, UC2On центров масс С1, С2 соударяющихся тел в конце удара на главную нормаль.
4. Определить коэффициент восстановления при ударе по формуле k = 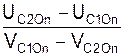 .
.
Дата добавления: 2015-05-30; просмотров: 1850;
