Гироскоп с тремя степенями свободы

Гироскопом называют симметричное твёрдое тело, угловая скорость вращения которого относительно оси симметрии значительно превосходит по модулю угловую скорость вращения оси симметрии.

I I = ω₁ >> I I = ω₂,

где ω₁, ω₂ – модули угловых скоростей , .

В современных гироскопических приборах частота n₁ вращения относительно оси симметрии (оси гироскопа) достигает значений 40000 – 50000 об/мин (ω₁ = 4200 – 5200 рад/с), а частота n₂ вращения оси симметрии равна одному обороту за 2 – 3 минуты (n₂ = 3, 14 – 4, 73 об/мин) и даже за 20 минут (n₂ = 0,314 об/мин) для гирокомпасов.

Рассмотрим случай, когда гироскоп движется в инерциальной системе отсчёта O₂X₂Y₂Z₂ около неподвижной точки О₂ (рис. 7.1).

На рис. 7.1 приняты условные обозначения: O₂X₂Y₂Z₂ – инерциальная система отсчёта (ИСО); O₁X₁Y₁Z₁ – подвижная система отсчёта (ПСО); – вектор угловой скорости вращения гироскопа относительно оси симметрии (ось симметрии гироскопа совпадает с осью O₁Z₁ подвижной системы отсчёта); 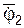– вектор угловой скорости вращения оси O₁Z₁ симметрии гироскопа относительно оси O₂Z₂ инерциальной системы отсчёта O₂X₂Y₂Z₂; θ – угол наклона оси O₁Z₁ симметрии к оси O₂Z₂ инерциальной системы отсчёта (угол нутации); L_O( ) – кинетический момент гироскопа относительно точки О при его вращении вокруг оси симметрии O₁Z₁ с угловой скоростью ; L_O( 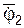) – кинетический момент гироскопа относительно точки О при его вращении вокруг оси O₂Z₂ инерциальной системы отсчёта O₂X₂Y₂Z₂ с угловой скоростью ; L_O – кинетический момент гироскопа относительно точки О при его вращении с угловой скоростью вокруг мгновенной оси вращения OZ₃; – вектор угловой скорости вращения гироскопа относительно мгновенной оси вращения OZ₃.

Начала О₁ подвижной системы отсчёта O₁X₁Y₁Z₁ и О₂ инерциальной системы отсчёта O₂X₂Y₂Z₂ помещены в точку О.

Гироскоп вращается с угловой скоростью относительно оси O₁Z₁ симметрии, которая в свою очередь вращается с угловой скоростью относительно оси O₂Z₂ инерциальной системы отсчёта O₂X₂Y₂Z₂.

Вектор абсолютной угловой скорости гироскопа определяют по формуле = + 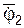. При этом вектор лежит на мгновенной оси OZ₃ вращения гироскопа.

Кинетический момент L_O гироскопа относительно точки О равен

L_O = L_O( ) + L_O( ).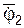

В развёрнутом виде последняя формула выглядит следующим образом:

L_O = J_O1Z1·( ) + J_O2Z2·( ),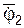

где J_O1Z1, J_O2Z2 – моменты инерции гироскопа относительно осей O₁Z₁, O₂Z₂.

Так как I I << I I, то величина угла θ очень мала (в современных приборах она составляет доли секунды). Тогда с достаточной для инженерной практики точностью можно считать, что

L_O( 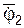) = J_O2Z2·( 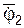) = 0.

С учётом этого допущения имеем

L_O = J_O1Z1·( ).

На таком допущении основана приближённая (элементарная) теория гироскопов.

При решении задач с помощью приближённой теории гироскопов удобно пользоваться теоремой Резаля, которая выражается формулой

dL_O/dt = U = Σ M_O(F_i^E) + Σ M_O(R_i^E) = ,

где L_O – кинетический момент гироскопа относительно точки О; U – скорость конца вектора L_O в инерциальной системе отсчёта; Σ M_O(F_i^E), Σ M_O(R_i^E) – геометрические суммы моментов активных сил F_i^E и реакций R_i^E внешней связи относительно точки О; – главный момент внешних сил, приложенных к гироскопу, относительно точки О.

Скорость U конца вектора L_O кинетического момента гироскопа относительно точки О направлена так же , как и вектор главного момента внешних сил , приложенных к гироскопу, относительно той же точки.

Использование теоремы Резаля позволяет решать следующие задачи: 1) по известным активным силам F_i^E и реакциям R_i^E внешней связи определяют направление движения оси симметрии гироскопа; 2) по известному закону движения оси гироскопа определяют главный момент внешних сил .

Пример 1.

Определить направление движения оси симметрии гироскопа, если к ней приложена активная сила F_i^E, которая параллельна плоскости OYZ.

Решение.

Приложим к гироскопу активную силу F_i^E, силу тяжести G и реакции X_O, Y_O, Z_O внешней связи в точке О (рис. 7.4).

= Σ M_O(F_i^E) + Σ M_O(G) + Σ M_O(X_O) + Σ M_O(Y_O) + Σ M_O(Z_O).

Так как Σ M_O(G) = 0, Σ M_O(X_O) = 0; Σ M_O(Y_O) = 0, Σ M_O(Z_O) = 0, то имеем

= Σ M_O(F_i^E).

Главный момент внешних сил относительно точки О приложен в этой точке и направлен по оси ОХ в сторону увеличения координаты Х (напомним, что момент силы относительно точки направляется перпендикулярно плоскости, проходящей через силу и точку так, что с его конца видно, что сила стремится повернуть тело вокруг точки против хода часовой стрелки).

Кинетический момент L_O = J_OZ· гироскопа относительно точки О направлен в сторону вектора угловой скорости вращения. Конец вектора L_O обозначим точкой D.

Применив теорему Резаля U = , направляем вектор U скорости точки D параллельно вектору .

Таким образом, ось OZ симметрии гироскопа будет перемещаться в плоскости OXZ, которая перпендикулярна направлению активной силы F_i^E.

Пример 2.

Рассмотрим движение гироскопа в инерциальной системе отсчёта OXYZ (рис. 7.6).

Приложим к гироскопу активную силу G (силу тяжести) и реакции X_O, Y_O, Z_O внешней связи в точке О. Модуль 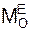главного момента внешних сил, приложенных к гироскопу, равен

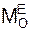= G·OC·sin(θ).

Вектор главного момента внешних сил направлен по оси OY в сторону увеличения координаты Y.

Кинетический момент L_O гироскопа относительно точки О направлен по оси симметрии в сторону вектора угловой скорости и равен по модулю

L_O = J_O1Z1·ω,

Обозначим точкой D конец вектора L_O. Согласно теореме Резаля, U = . Поэтому U – скорость точки D направлена перпендикулярно к оси симметрии (параллельна оси ОХ) в сторону увеличения координаты Х. Модуль U скорости U равен

U = 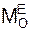= G·OC·sin(θ) = const.

Таким образом, точка D имеет постоянную по модулю скорость U, направленную перпендикулярно к вертикальной плоскости, содержащей ось симметрии гироскопа. При этом ось гироскопа описывает боковую поверхность кругового конуса, поворачиваясь относительно вертикальной оси OZ с угловой скоростью . Это движение называют регулярной прецессией оси гироскопа.

Вычислим модуль ω₁ угловой скорости регулярной прецессии.

ω₁ = I I = U/(DA) = = = .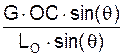

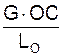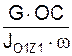Окончательно имеем

ω₁ = .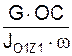

Чем меньше модуль ω угловой скорости вращения гироскопа относительно его оси симметрии, тем больше модуль ω₁ угловой скорости прецессии (от величины угла θ угловая скорость прецессии не зависит).

Задачи на определение движения оси гироскопа с помощью приближённой теории рекомендуется решать по следующему алгоритму.

1. Проверить, имеет ли гироскоп три степени свободы.

2. Выбрать систему координат.

3. Изобразить на рисунке внешние силы, приложенные к гироскопу.

4. Определить главный момент внешних сил относительно неподвижной точки О.

5. Найти кинетический момент L_O гироскопа относительно неподвижной точки О.

6. Применив теорему Резаля U = , определить движения оси гироскопа.

В экзаменационных задачах, как правило, требуется определить ω, J_O1Z1, ОС. Эти величины определяют по формулам:

ω₁ = ;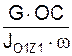

J_O1Z1 = ;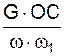

ОС = .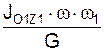

Пример 3.

На рис. 7.7 приведена схема гироскопа в кардановом подвесе. Конструктивная схема содержит корпус 1, уравновешенный массивный круглый цилиндр, горизонтальную 3 и вертикальную рамки.

Тело 2 вращается с угловой скоростью в подшипниках горизонтальной рамки 3 относительно оси ОХ. Рамка 3 может поворачиваться в подшипниках рамки 4 относительно оси OY. В свою очередь рамка 4 может поворачиваться в подшипниках корпуса 1 гироскопа относительно оси OZ. Координатные оси OX, OY, OZ пересекаются в центре масс механической системы, состоящей из тел 2, 3, 4.

Если точки О и С совпадают, то такой гироскоп называют астатическим (уравновешенным), в противном случае – тяжёлым.

Определить изменение положения оси ОХ вращения тела 2, пренебрегая трением в подшипниках.

Решение.

Гироскоп в кардановом подвесе имеет три степени свободы, так как его положение определяется тремя независимыми углами поворота относительно осей OX, OY, OZ, пересекающихся в центре С масс механической системы, состоящей из тел 2, 3, 4. При этих условиях главный момент внешних сил относительно точки О равен нулю: ( = 0). Кинетический момент L_O гироскопа направлен по оси ОХ. Конец вектора L_O обозначим точкой D (см. рис 7.7).

Применив теорему Резаля (U = ), находим U = 0, т. е. скорость точки U равна нулю. Это означает, что при вращении массивного тела 2 ось ОХ гироскопа сохраняет неизменное положение в пространстве.

Таким образом, ответ на вопрос, поставленный в задаче, получен.