Вынужденные колебания систем с одной степенью свободы

Если при действии динамической нагрузки P=P(t) не учитывать силы сопротивления, то получим дифференциальное уравнение второго порядка с постоянными коэффициентами

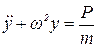. (1)

Общее решение этого уравнения равно сумме общего решения однородного уравнения и частного решения неоднородного уравнений:

y = y_од +y_ч ,

где y_од совпадает с решением уравнения собственных колебаний, а частное решение зависит от вида динамической нагрузки. Последнее будем искать разложением нагрузки на сумму мгновенных импульсов.