Удар – механическое взаимодействие материальных тел, приводящее к конечному изменению скоростей их точек за бесконечно малый промежуток времени.
Примечание. Этот промежуток времени называют временем удара.
В теории удара классической механики вводится следующая идеализация этого процесса – совершается предельный переход к бесконечно большим силам, действующим бесконечно малое время (ударные силы) и имеющим конечный импульс S.
Ударная сила – сила, импульс которой за время удара является конечной величиной.
Ударный импульс – импульс ударной силы за время удара.
В технической литературе зачастую ударные силы называют мгновенными силами.
Согласно известным утверждениям кинематики поступательное движение твёрдого тела имеет такие же уравнения движения, как и точка. Рассмотрим движение материальной точки массой m в инерциальной системе отсчёта OXYZ под действием силы тяжести G и активной силы FiE на участке АВ (рис. 8.2).
 |
В момент времени, когда материальная точка занимает на траектории её движения положение В, происходит удар. В этом положении материальная точка получает конечное изменение скорости от V1 до V2. В момент удара на материальную точку кроме сил G и FiE действует ударная сила Р. В отличие от ударной силы Р, силы FiE и G называют немгновенными силами.
В положении В, где действовала ударная сила Р, происходит резкое изменение траектории движения АВD точки. После прекращения действия ударной силы Р материальная точка на участке ВD снова движется под действием силы тяжести G и активной силы FiE.
Таким образом, в теории удара классической механики сделаны следующие допущения.
1. Действие немгновенных сил за время удара не учитывают.
2. Перемещение материальной точки за время удара не учитывают.
3. Результат действия ударной силы на материальную точку выражается в скачкообразном (конечном) изменении за время удара вектора её скорости, которое описывается векторным равенством V2 = V1 + (S/m).

В действительности скачок скорости происходит в течение очень малого промежутка времени. Рассмотрим взаимодействие двух тел, совершающих поступательное движение в момент удара (рис. 8.3), и введём понятия, широко используемые в инженерной практике.
Линия центров – линия, проходящая через центры масс соударяющихся тел.
Центральный удар – удар, при котором линия действия ударного импульса, приложенного к ударяемому телу, проходит через его центр масс.
Прямой удар – удар, при котором скорости центров масс соударяющихся тел лежат на линии центров.
Косой удар – удар, при котором хотя бы одна из скоростей центров масс соударяющихся тел не лежит на линии центров.
Рассмотрение процесса удара требует выхода из рамок классической механики – отказа от схемы абсолютно твёрдого тела и перехода к схеме деформируемого тела. В зависимости от степени восстановления недеформированного состояния удары разделяются на абсолютно неупругие, упругие и абсолютно упругие.
Абсолютно неупругий удар – удар, при котором недеформированное состояние соударяющихся тел не восстанавливается.
В конце неупругого удара центры тяжести соударяющихся движутся с одинаковыми скоростями.
Упругий удар – удар, при котором недеформированное состояние тел восстанавливается не полностью.
В конце упругого удара центры тяжести соударяющихся тел движутся с разными скоростями.
Абсолютно упругий удар – удар, при котором недеформированное состояние соударяющихся тел восстанавливается полностью.
В конце абсолютно упругого удара центры тяжести соударяющихся тел движутся с разными скоростями.
Рассмотрим прямой центральный упругий удар двух тел. На рис. 8.4 изображена расчётная схема этого удара. До удара (см. рис. 8.4,а) соударяющиеся тела 1 и 2 движутся в одном направлении с абсолютными скоростями VC1, VC2 центров С1, С2 масс этих тел. На рис. 8.4,б изображен момент удара тел 1 и 2. Расчётная схема движения тел после удара приведена на рис. 8.4,в.
Напомним, что абсолютной скоростью называют скорость в инерциальной системе отсчёта.
Процесс упругого удара разделим на два этапа. В течение первого этапа (см. рис. 8.4,б) совершается деформация соударяющихся тел. В течение второго этапа – частичное восстановление недеформированного состояния. В момент окончания первого этапа и начала второго центры масс тел обладают одинаковыми скоростями, которые они имели бы в конце соответствующего абсолютно неупругого удара. В конце второго этапа центры масс тел имеют другие абсолютные скорости UС1, UС2.

Отношение изменений скоростей тел после удара к скоростям тел до удара характеризуется коэффициентом восстановления при ударе.
Коэффициент восстановления при ударе – величина, равная модулю отношения разности проекций скоростей центров масс тел на нормаль после удара к разности проекций скоростей центров масс тел на нормаль до удара.
Величину коэффициента k определяют по формуле
k = 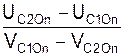 ,
,
где UC2On, UC1On – проекции абсолютных скоростей центров масс тел 2 и 1 на главную нормаль после удара; VC1On, VC2On – проекции абсолютных скоростей центров масс тел 1 и 2 до удара.
Коэффициент восстановления, являющийся безразмерной величиной, изменяется в пределах от 0 до 1 (0 < k < 1); при абсолютно неупругом ударе k = 0, при упругом ударе k < 1, при упругом ударе k = 1.
 |
Рассмотрим косой центральный удар двух тел (рис. 8.5).
При рассмотрении косого центрального упругого удара поступательно движущихся твёрдых тел поверхности соударяющихся тел будем считать абсолютно гладкими.
До удара (см. рис. 8.5а) абсолютные скорости VC1, VC2 центров С1, С2 центров масс тел 1 и 2 направлены к линии центров под углами α1, α2. После удара (см. рис. 8.5,б) абсолютные скорости UC1, UC2 центров масс тел 1 и 2 направлены к линии центров под углами β1, β2.
Величину коэффициента k при косом ударе определяют по формуле
k = 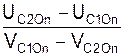 =
= 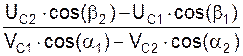 .
.
Дата добавления: 2015-05-30; просмотров: 1738;
