Уравнения Лагранжа второго рода
Уравнения Лагранжа второго рода – дифференциальные уравнения движения механической системы в обобщённых координатах.
Для механической системы с n степенями свободы эти уравнения имеют вид
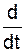(∂TS/∂ 
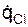) – ∂TS/∂qCi = Qqci, i = 1, …, n,
где ТS – кинетическая энергия механической системы; qCi – обобщённая координата; 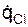– обобщённая скорость; Qqci – обобщённая сила по обобщённой координате qCi.
Число уравнений Лагранжа второго рада равно числу степеней свободы рассматриваемой механической системы.
Используя рис 6.30, поясним понятия «обобщённая скорость», «обобщённая сила».
На рис. 6.30 приняты условные обозначения: 
– активная сила, приложенная к точке механической системы; δqCi – приращение обобщённой координаты qCi (возможное перемещение i-й точки системы); 
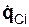– обобщённая скорость i-й точки механической системы.
Обобщённая скорость – производная по времени от обобщённой координаты.
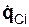= dqCi/dt.
Определим возможную элементарную работу δАS( ) активных сил , приложенных к точкам механической системы при задании какой-либо её точке возможного перемещения δqCi.
δАS( ) = Σ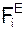 
·δqCi·cos( , δqCi).
Обобщенная сила Qqci по обобщенной координате qCi – величина, равная отношению возможной элементарной работы δАS активных сил , приложенных к точкам механической системы, к модулю δqСi приращения обобщённой координаты qCi.
Qqi = δAS( )/δqCi.
Формулировка уравнения Лагранжа второго рода.
Разность полной производной по времени от частной производной кинетической энергии по обобщенной скорости и частной производной от кинетической энергии по обобщенной координате равна обобщенной силе.
Уравнения Лагранжа второго рода используют в качестве универсального метода составления дифференциальных уравнений движения механических систем любой степени сложности. Преимущество этого метода по сравнению с применяемыми ранее общими теоремами динамики заключается в том, что в уравнениях Лагранжа второго рода используются только активные силы. Это намного упрощает решение задач динамики механических систем.
Согласно учебной программе выполнение курсового задания на применение уравнений Лагранжа второго рода к исследованию движения механических систем не предусмотрено. Тем не менее для развития общего кругозора студента приведём пример решения такого типа задач.
Пример.
Однородный барабан 1 массой m1 и радиусом R1 приводится во вращение активным моментом М. На барабан наматывается невесомый трос, перекинутый через невесомый блок 2. К свободному концу троса прикреплён груз 3 массой m3 (рис. 6.31).
Механическая система начинает двигаться из состояния покоя. Составить дифференциальное уравнение вращательного движения барабана.
Дано: m1 = 20 кг; R1 = 0,2 м; m3 = 10 кг; М = 200 Н·м.
 |
Решение.
Механическая система имеет одну степень свободы. Примем за обобщённую координату q угол φ1 поворота тела 1 (рис. 6.32).
Запишем уравнение Лагранжа второго рода для рассматриваемой механической системы.
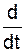(∂TS/∂ 
) – ∂TS/∂φ1 = Qφ1,
где ТS – кинетическая энергия механической системы; Qφ1 – обобщённая сила по обобщённой координате φ1; – обобщённая скорость.
Зададим приращение δφ1 обобщённой координате φ1. Тогда центр масс тела 3 получит возможное перемещение
δSС3 = δφ1·R1.
Кинетическая энергия механической системы равна
ТS = Т1 + Т3,
где Т1 – кинетическая энергия барабана 1; Т3 – кинетическая энергия груза 3.
Тело 1 совершает вращательное движение относительно оси С1Х1. Его кинетическую энергию определим по формуле
T1 = 0,5·JC1X1·( )2 = 0,5·(m1·(R1)2/2)·( )2 = 0,25·m1·(R1)2·( )2.
Согласно рис. 6.32 тело 3 совершает поступательное движение. Исходя из этого утверждения, его кинетическую энергию определим по формуле
T3 = 0,5·m3·(VC3)2 = 0,5·m3·( ·R1)2.
В последней формуле символом VC3 обозначена скорость центра масс тела 3.
Кинетическая энергия механической системы
ТS = 0,25·m1·(R1)2·( )2 + 0,5·m3·( ·R1)2 =
= (0,25·m1 + 0,5·m3)·( ·R1)2.
Определим частную производную от кинетической энергии механической системы по обобщённой скорости .
∂TS/∂ = 2·(0,25·m1+ 0,5·m3)·(R1)2· 
.
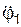Тогда
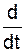(∂TS/∂ ) = (0,5·m1+ m3)·(R1)2· .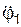
Так как кинетическая энергия системы не зависит от обобщённой координаты φ1, то соответственно её частная производная ∂TS/∂φ1 равна нулю (∂TS/∂φ1 = 0).
Тогда левая часть уравнения Лагранжа вторго рода равна
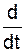(∂TS/∂ ) – ∂TS/∂φ1 = (0,5·m1+ m3)·(R1)2· .
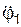Определим элементарную работу δАS( ) сил, приложенных к механической системе на её возможном перемещении.
δАS( ) = M·δφ1 – G3·δSC3 = M·δφ1 – m3·g·δφ1·R1 =
= (M – m3·g·R1)·δφ1.
Согласно определению обобщённая сила Qφ1 по обобщённой координате φ1 равна
Qφ1 = δАS/ δφ1 = M – m3·g·R1.
Уравнение Лагранжа второго рода для рассматриваемой механической системы принимает вид
(0,5·m1+ m3)·(R1)2· 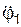= M – m3·g·R1.
Решая это уравнение относительно углового ускорения 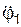, получим
= 
=
= 
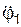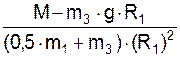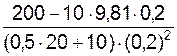= 17,344 м/с2.
Дважды интегрируя эти дифференциальные уравнения и определив постоянные интегрирования, получим:
= 17,344·t; φ1 = 8,672·t2.
Дата добавления: 2015-05-30; просмотров: 2146;