Задачи на применение принципа возможных перемещений рекомендуется решать по следующему алгоритму.
1. Изобразить рассматриваемую механическую систему на рисунке в соответствующем масштабе.
2. Приложить к механической системе активные нагрузки.
3. При наличии неидеальных связей добавить соответствующие реакции связей (например, силы трения).
4. Для определения реакции связи эту реакцию перенести в разряд активных сил путём замены существующей связи на связь, допускающую возможное перемещение в направлении, как правило, противоположном направлению определяемой реакции связи.
5. Задать возможное перемещение одной из точек механической системы и выразить возможные перемещения точек приложения сил в зависимости от заданного возможного перемещения.
6. Вычислить сумму работ активных сил на возможных перемещениях их точек приложения и приравнять эту сумму нулю.
7. Решив составленное уравнение, определить искомую величину.
Пример.
На рис. 6.17 изображена механическая система, находящаяся в равновесии. Определить модуль силы F, приложенной в точке А рычага 1.
Дано: G5 = 100 H; α = 30о; d1 = 1 м; b1 = 0,5 м; d3 = 0,8 м;
 |
b3 = 0,5 м.
Решение.
Согласно рис. 6.17 механическая система, содержащая пять тел, имеет одну степень свободы. Наложенные на эту систему в точках С и К связи (шарнирно-неподвижные опоры) являются идеальными. На механическую систему, находящуюся в равновесии, действуют активные силы F и G5.

Зададим возможное угловое перемещение δφ1 телу 1, которое может совершать вращательное движение (рис. 6.18).
Модули возможных перемещений δSA , δSB точек А и В в зависимости от δφ1 определим по формулам:
δSA = δφ1·АС = δφ1·d1; δSB= δφ1·BC = δφ1·b1.
Решая совместно эти выражения, найдем зависимость
δSB= f(δSA) = δSA·b1/d1.
Из условия принадлежности точки D телу 3, которое получит возможное угловое перемещение δφ3, эта точка получит возможное перемещение δSD, перпендикулярное отрезку DK.
δSD = δφ3·DK = δφ3·d3.
Рассмотрим элементарное движение тела 2. Это тело совершает мгновенно поступательное движение, так как возможные перемещения δSB, δSD соответствующих точек этого тела одинаково направлены. Исходя из этого, имеем
δSD = δSB = δφ3·d3 = δSA·b1/d1.
Точка Е тела 3 получит возможное перемещение δSЕ, модуль δSЕ которого определим по формуле
δSЕ = δφ3·ЕK = δφ3·b3.
Выразим модуль возможного перемещения δSЕ точки Е сначала в зависимости от модуля возможного перемещения δSD точки D, а затем в зависимости от модуля возможного перемещения δSА точки А:
δSЕ = δSD·(b3/d3) = 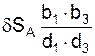 .
.
Так как участок нити EL и груз 5 совершают поступательные движения, то имеем
δSЕ = δSL = δSC5 = 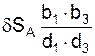 ,
,
где δSL, δSC5 – соответственно возможные перемещение точки L, принадлежащей нити 4 и центру С5 масс груза 5.
Запишем принцип возможных перемещений для рассматриваемой механической системы.
ΣFi·δSi·cos(Fi, δSi) = 0 = F·δSА·cos(α) – G5·δSC5 = 0.
Так как δSC5 = 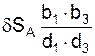 , то получим
, то получим
F·δSА·cos(α) – G5· 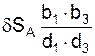 = 0.
= 0.
Решая последнее выражение, определим модуль силы F, при котором механическая система находится в равновесии.
6.3.3. Варианты курсового задания Д 7
«Применение принципа возможных перемещений
к определению реакций опор составной конструкции»
Применяя принцип возможных перемещений, определить реакции опор составной конструкции. Схемы конструкций и необходимые для решения данные приведены в табл. 5.5. На рисунках все размеры указаны в метрах.
Таблица 5.5
| Номер варианта | Расчётная схема механизма | Исходные данные |
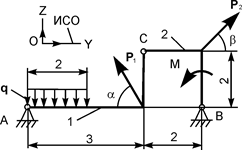
| Р1 = 10 кН; Р2 = 10 кН; М = 6 кН·м; q = 2 кН/м | |
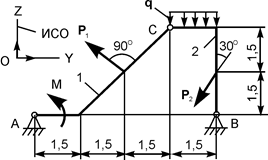
| Р1 = 6 кН; Р2 = 10 кН; М = 12 кН·м; q = 1 кН/м | |
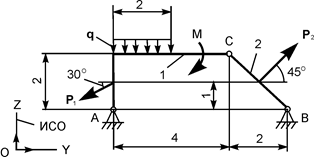
| Р1 = 8 кН; Р2 = 10 кН; М = 3 кН·м; q = 2 кН/м |
Продолжение табл. 5.5
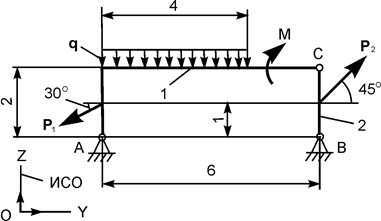
| Р1 = 5 кН; Р2 = 12 кН; М = 4 кН·м; q = 2 кН/м | |
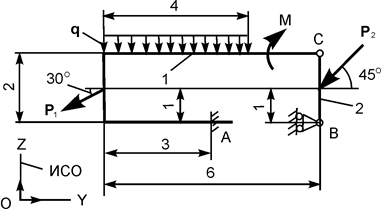
| Р1 = 6 кН; Р2 = 8 кН; М = 3 кН·м; q = 2 кН/м | |
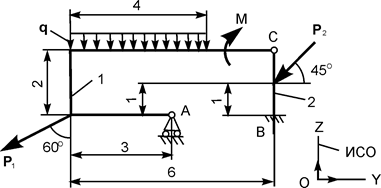
| Р1 = 4 кН; Р2 = 6 кН; М = 10 кН·м; q = 2 кН/м |
Продолжение табл. 5.5
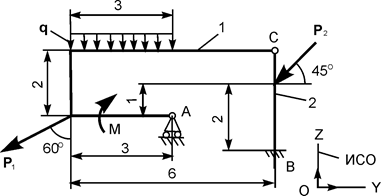
| Р1 = 7 кН; Р2 = 8 кН; М = 15 кН·м; q = 2 кН/м | |
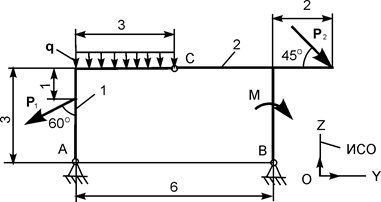
| Р1 = 8 кН; Р2 = 8 кН; М = 16 кН·м; q = 2 кН/м | |
| Р1 = 10 кН; Р2 = 10 кН; М = 6 кН·м; q = 2 кН/м |
Продолжение табл. 5.5
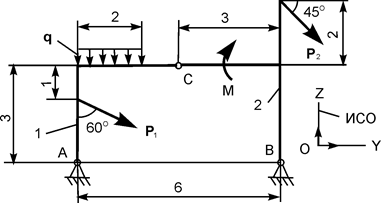
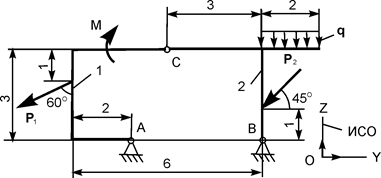
| Р1 = 10 кН; Р2 = 3 кН; М = 9 кН·м; q = 2 кН/м | |
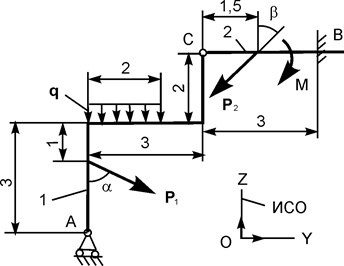
| Р1 = 12 кН; Р2 = 5 кН; М = 6 кН·м; q = 1 кН/м | |
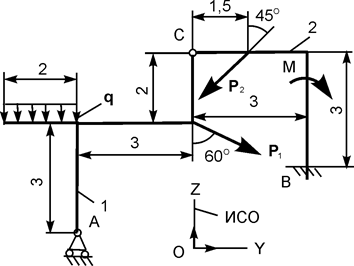
| Р1 = 11 кН; Р2 = 3 кН; М = 8 кН·м; q = 4 кН/м |
Продолжение табл. 5.5
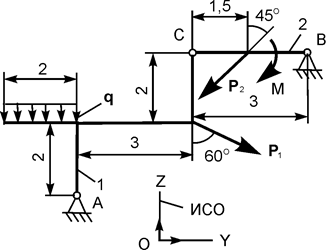
| Р1 = 10 кН; Р2 = 12 кН; М = 8 кН·м; q = 2 кН/м | |
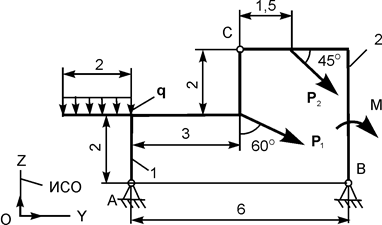
| Р1 = 10 кН; Р2 = 2 кН; М = 12 кН·м; q = 2 кН/м | |
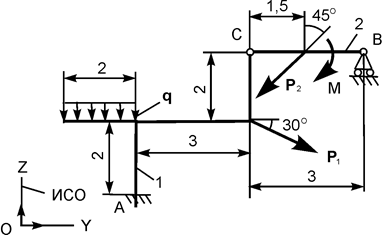
| Р1 = 15 кН; Р2 = 10 кН; М = 5 кН·м; q = 2 кН/м |
Продолжение табл. 5.5
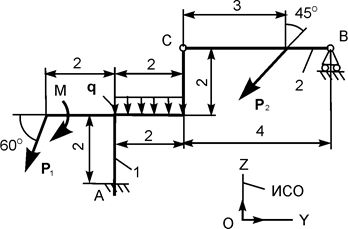
| Р1 = 16 кН; Р2 = 10 кН; М = 4 кН·м; q = 1 кН/м | |
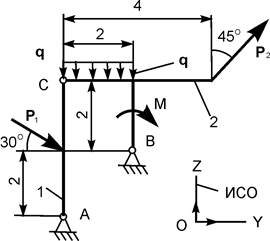
| Р1 = 17 кН; Р2 = 3 кН; М = 6 кН·м; q = 6 кН/м | |
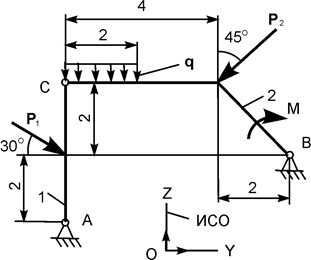
| Р1 = 18 кН; Р2 = 9 кН; М = 4 кН·м; q = 8 кН/м |
Продолжение табл. 5.5
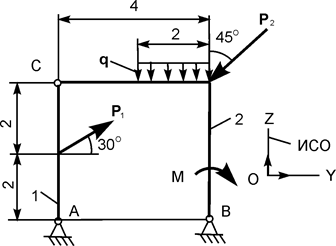
| Р1 = 19 кН; Р2 = 7 кН; М = 12 кН·м; q = 2 кН/м | |
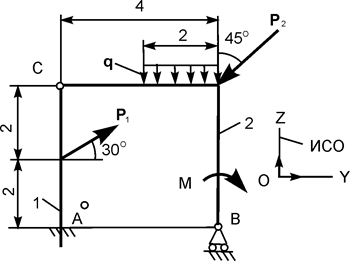
| Р1 = 20 кН; Р2 = 12 кН; М = 8 кН·м; q = 4 кН/м | |
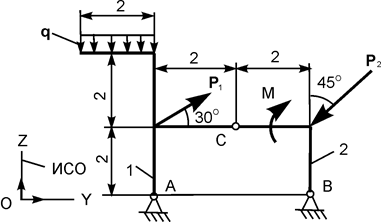
| Р1 = 21 кН; Р2 = 10 кН; М = 12 кН·м; q = 6 кН/м |
Продолжение табл. 5.5
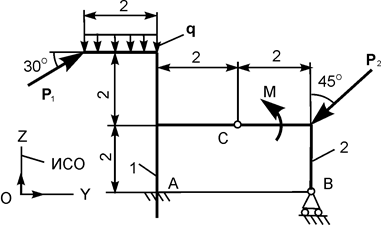
| Р1 = 22 кН; Р2 = 12 кН; М = 10 кН·м; q = 5 кН/м | |
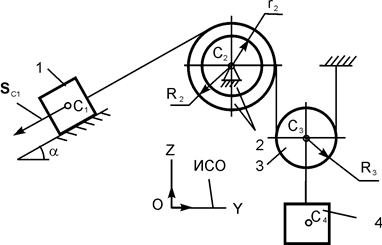
| Р1 = 23 кН; Р2 = 9 кН; М = 5 кН·м; q = 8 кН/м | |
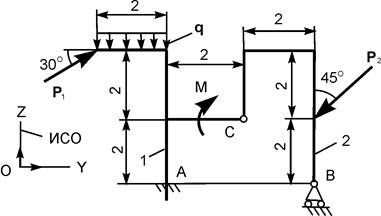
| Р1 = 24 кН; Р2 = 10 кН; М = 12 кН·м; q = 2 кН/м |
Продолжение табл. 5.5
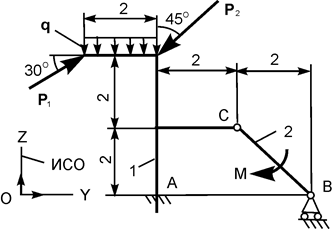
| Р1 = 25 кН; Р2 = 10 кН; М = 8 кН·м; q = 2 кН/м | |
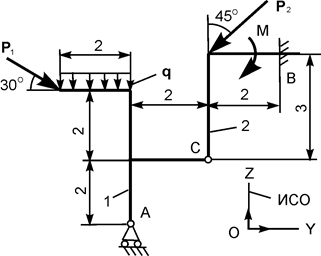
| Р1 = 26 кН; Р2 = 16 кН; М = 6 кН·м; q = 6 кН/м | |
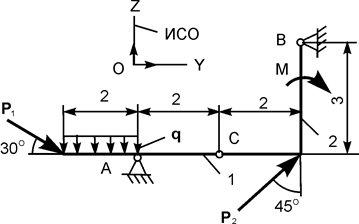
| Р1 = 27 кН; Р2 = 10 кН; М = 4 кН·м; q = 3 кН/м |
Окончание табл. 5.5
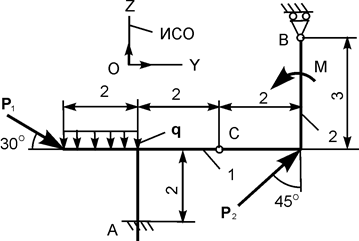
| Р1 = 28 кН; Р2 = 18 кН; М = 8 кН·м; q = 2 кН/м | |
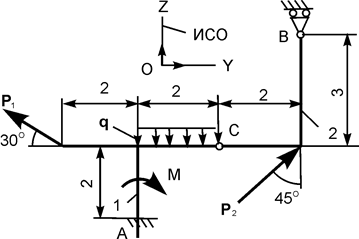
| Р1 = 28 кН; Р2 = 20 кН; М = 6 кН·м; q = 2 кН/м | |
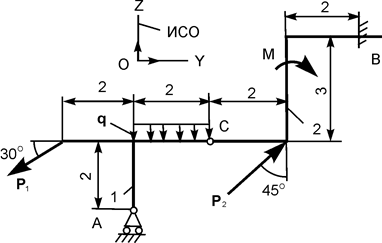
| Р1 = 30 кН; Р2 = 20 кН; М = 6 кН·м; q = 1 кН/м |
6.3.4. Пример выполнения курсового задания Д 7
 |
Дано: конструкция, состоящая из двух тел, находится в равновесии под действием следующих нагрузок: Р1 = 2 кН; Р2 = 4 кН; М = 6 кН·м; q = 1 кН/м (рис. 6.19).
Применяя принцип возможных перемещений, определить реакции опор составной конструкции.
Решение.

Заменим равномерно распределённую нагрузку интенсивностью q сосредоточенной силой Q, приложенной в середине загруженного участка тела 1 (рис. 6.20). Модуль этой силы определим по формуле Q = q·2 = 1·2 = 2 кН.
Поскольку связи, наложенные на рассматриваемую механическую систему, являются идеальными, то для решения поставленной задачи правомерно применение принципа возможных перемещений.
Найдем горизонтальную составляющую ХА реакции в жёсткой заделке.
Согласно известным положениям статики жёсткая заделка накладывает три ограничения на перемещения тела в плоскости OXY (поступательные движения параллельно координатным осям и поворот в этой плоскости). Снимем ограничение на перемещение тела 1 только параллельно оси ОХ, сохраняя другие ограничения, и покажем на рисунке реакцию ХА. В результате этих действий реакция ХА переходит в разряд активных сил, а жёсткая заделка в точке А (см. рис. 6.19) заменяется кулисным камнем, к которому жёстко закреплено тело 1 составной конструкции. При такой замене составная конструкция становится подвижной.
Зададим возможное перемещение δSA точке А тела 1. Так как тело 1 может совершать только поступательное движение, то возможные перемещения всех точек этого тела геометрически равны:
δSA = δSP1 = δSQ = δSC,
где δSP1 – возможное перемещение точки приложения силы Р1; δSQ – возможное перемещение точки приложения силы Q; δSC – возможное перемещение точки С.
Так как точка С принадлежит и телу 2, то оно тоже будет подвижным. Для того, чтобы связь в точке В не разрушилась, эта точка получит возможное перемещение δSВ, параллельное опорной поверхности шарнирно-подвижной опоры. Поскольку возможные перемещения δSC, δSВ точек С и В тела 2 параллельны, то тело 2 совершает поступательное движение. Исходя из этого, имеем следующее равенство:
δSC = δSВ = δSР2,
где δSР2 – возможное перемещение точки приложения силы Р2.
Таким образом, возможные перемещения всех точек тел 1 и 2 геометрически равны:
δSA = δSP1 = δSQ = δSC = δSВ = δSР2.
Запишем уравнение, выражающее принцип возможных перемещений для рассматриваемого случая.
ΣFi·δSi·cos(Fi, δSi) = 0 = – XA·δSA + P1·δSP1 – P2·cos(45о)·δSР2 = 0. (1)
Поскольку δSA = δSP1 = δSР2, то выражение (1) можно записать в следующем виде:
– XA·δSA + P1·δSА – P2·cos(45о)·δSА = 0.
Решая последнее выражение относительно ХА, получим
XA = P1 – P2·cos(45о) = 2 – 4·0,707 = – 0,828 кН.
Найдем вертикальную составляющую YА реакции в жёсткой заделке.

Согласно известным положениям статики жёсткая заделка накладывает три ограничения на перемещения тела в плоскости OXY (поступательные движения параллельно координатным осям и поворот в этой плоскости). Снимем ограничение на перемещение тела 1 только параллельно оси ОY, сохраняя другие ограничения, и покажем на рисунке реакцию YА. В результате этих действий реакция YА переходит в разряд активных сил, а жёсткая заделка в точке А (рис. 6.21) заменяется кулисным камнем, к которому жёстко закреплено тело 1 составной конструкции. При такой замене составная конструкция становится подвижной.
Зададим возможное перемещение δSA точке А тела 1. Так как тело 1 может совершать только поступательное движение, то возможные перемещения всех точек этого тела геометрически равны:
δSA = δSP1 = δSQ = δSC,
где δSP1 – возможное перемещение точки приложения силы Р1; δSQ – возможное перемещение точки приложения силы Q; δSC – возможное перемещение точки С.
Так как точка С принадлежит и телу 2, то оно тоже будет подвижным. Для того, чтобы связь в точке В не разрушилась, эта точка должна получить возможное перемещение δSВ, параллельное опорной поверхности шарнирно-подвижной опоры. Поскольку возможные перемещения δSC, δSВ точек С и В тела 2 не параллельны, то тело 2 совершает плоскопараллельное движение. Очевидно, что мгновенный центр поворота тела 2 находится в точке В. Относительно оси, проходящей через точку В и перпендикулярной плоскости рис. 6.21, тело 2 повернётся на угол δφ2. Исходя из этого, имеем следующее равенство:
δSC = CB·δφ2 = 3·δφ2.
Следует заметить, что возможные перемещения δSC, δSP2 точки С и точки приложения силы Р2 перпендикулярны отрезкам, соединяющим эти точки с мгновенным центром поворота тела 2.
Принцип возможных перемещений выражается формулой
∑Fi·δSi·cos(Fi, δSi) = 0.
Так как величину угла между направлениями активной силы Р2 и возможным перемещением δSP2 точки приложения этой силы определять достаточно затруднительно, то элементарную работу приложенных к телу 2 сил определим через работу моментов сил относительно его мгновенного центра поворота, который расположен в точке В. С этой целью силу Р2 разложим на составляющие силы: P2·sin(45о) и P2·cos(45о).
Запишем уравнение, выражающее принцип возможных перемещений:
– YA·δSA + Q·δSQ + P2·sin(45о)·1,5·δφ2 +
+ P2·cos(45о)·3·δφ2 – M·δφ2 = 0. (2)
Так как δSA = δSQ = 3·δφ2, то выражение (2) можно преобразовать к следующему виду:
– YA·3·δφ2 + Q·3·δφ2 + P2·sin(45о)·1,5·δφ2 +
+ P2·cos(45о)·3·δφ2 – M·δφ2 = 0.
Решая последнее выражение относительно YA, получим
YA = Q 1+ P2·sin(45о)·0,5 + P2·cos(45о)·1 – M/3 =
= 2 1 + 4·0,707·0,5 + 4·0,707·1 – 6/3 = 4,242 кН.
Найдём реактивный момент МА в жёсткой заделке.
Жёсткая заделка накладывает три ограничения на перемещения тела в плоскости OXY (поступательные движения параллельно координатным осям и поворот в этой плоскости). Снимем ограничение на поворот тела 1 в плоскости ОХY, сохраняя другие ограничения, и покажем на рисунке реактивный момент МА. В результате этих действий реакция МА переходит в разряд активных нагрузок, а жёсткая заделка в точке А (рис. 6.22) заменяется шарнирно-неподвижной опорой. При такой замене составная конструкция становится подвижной. Тело 1 может совершать вращательное движение относительно оси, проходящей через точку А. Зададим телу 1 возможное угловое перемещение δφ1. Тогда точки приложения активных сил Р1, Q и точка С получат возможные перемещения δSP1, δSQ, δSC.
 |
δSP1 = 1,5·δφ1; δSQ = (
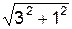 )·δφ1; δSC = CA·δφ1.
)·δφ1; δSC = CA·δφ1.
Следует отметить, что возможное перемещение δSC перпендикулярно отрезку, соединяющему точку С с осью вращения тела 1, проходящей через точку А.
Так как точка С принадлежит и телу 2, то оно тоже будет подвижным. Для того, чтобы связь в точке В не разрушилась, эта точка должна получить возможное перемещение δSВ, параллельное опорной поверхности шарнирно-подвижной опоры. Поскольку возможные перемещения δSC, δSВ точек С и В тела 2 не параллельны, то тело 2 совершает плоскопараллельное движение. Очевидно, что мгновенный центр поворота тела 2 находится в точке С2. Относительно оси, проходящей через точку С2 и перпендикулярную плоскости рис. 6.22, тело 2 повернётся на угол δφ2. Исходя из этого, имеем следующее равенство:
δSC = CС2·δφ2.
Так как точка С принадлежит и телу 1, и телу 2, то справедливо равенство
δSC = CA·δφ1 = CС2·δφ2.
Из рис. 6.22 нетрудно установить, что СА = СС2. Отсюда имеем
δφ1 = δφ2.
Возможные перемещения δSC, δSР2 точки С и точки приложения силы Р2 перпендикулярны отрезкам, соединяющим эти точки с мгновенным центром поворота тела 2.
В общем случае принцип возможных перемещений выражается формулой
∑Fi·δSi·cos(Fi, δSi) = 0.
Так как величину угла между направлениями активной силы Р2 и возможным перемещением δSP2 точки приложения этой силы определять достаточно затруднительно, то элементарную работу приложенных к телу 2 сил определим через работу моментов сил относительно его мгновенного центра поворота, который находится в точке С2. Как и ранее (см. рис. 6.21), силу Р2 разложим на составляющие силы: P2·sin(45о) и P2·cos(45о), параллельные координатным осям.
Запишем уравнение, выражающее принцип возможных перемещений.
– MA·δφ1 + P1·1,5·δφ1 – Q·1·δφ1 –
– P2·sin(45о)·1,5·δφ2 – P2·cos(45о)·6·δφ2 + M·δφ2 = 0. (3)
Поскольку δφ1 = δφ2, то выражение (3) можно преобразовать к виду
– MA·δφ1 + P1·1,5·δφ1 – Q·1·δφ1 –
– P2·sin(45о)·1,5·δφ1 – P2·cos(45о)·6·δφ1 + M·δφ1 = 0.
Решая это уравнение относительно МА, получим
MA = + P1·1,5 – Q·1 – P2·sin(45о)·1,5 – P2·cos(45о)·6 + M =
= 2·1,5 – 2·1 – 4·0,707·1,5 – 4·0,707·6 + 6 = – 14,210 кН·м.
Определим реакцию RB.
Шарнирно-подвижная опора в точке В накладывает только одно ограничение на перемещение тела 2 в пространстве. Снимем это ограничение на поступательное движение тела, параллельное оси ОY, и покажем на рис. 6.23 реакцию RB. Так как тело 1 неподвижно, то возможным перемещением тела 2 является его поворот относительно оси, проходящей через точку С на угол δφ2.
На рис. 6.23 показаны возможные перемещения δSВ, δSР2 точек приложения сил RB и Р2.
Составим уравнение, выражающее принцип возможных перемещений, при этом учтём, что работа силы при повороте тела равна произведению момента силы относительно мгновенного центра поворота на угол поворота тела.
P2·sin(45о)·1,5·δφ2 – P2·cos(45о)·3·δφ2 + M·δφ2 – RB·δSB = 0. (4)
Так как δSB = 3·δφ2, то выражение (4) приводится к виду
P2·sin(45о)·1,5·δφ2 – P2·cos(45о)·3·δφ2 + M·δφ2 – RB·3·δφ2 = 0.
 |
Решая последнее выражение относительно RB, получим
RB = P2·sin(45о)·0,5 – P2·cos(45о)·1 + M/3 =
= 4·0,707·0,5 – 4·0,707·1 + 6/3 = 0,586 кН.

Проведём проверку полученных результатов расчёта. Для этого рассмотрим равновесие составной конструкции под действием активных нагрузок Р1; Р2, М, Q и реакций внешних связей XA, YA, MA, RB (рис. 6.24).
Запишем уравнения равновесия для плоской произвольной системы сил и подставим в них определённые значения реакций внешних связей.
Σ  + Σ
+ Σ  = 0 = XA – P1 + P2·cos(45о) =
= 0 = XA – P1 + P2·cos(45о) =
= – 0,828 – 2 + 4·0,707 = – 2,828 + 2,828 = 0;
Σ  + Σ
+ Σ  = 0 = YA – P2·sin(45о) + RB =
= 0 = YA – P2·sin(45о) + RB =
= 4,242 – 2 – 4·+ 0,586 = 4,828 – 4,828 = 0;
ΣМА( 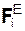 ) + ΣМА(
) + ΣМА( 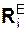 ) = 0 =
) = 0 =
= – MA + P1·1,5 – Q·1 – P2·sin(45о)·4,5 – M + RB·6 =
= – (–14,210) + 2·1,5 – 2·1 – 4·0,707·4,5 – 6 + 0,586·6 =
= 20,728 – 20,728 = 0.
Проверка подтвердила правильность расчётов.
Вопросы и задания для самоконтроля
1. Сформулировать определение понятия «обобщённые координаты механической системы».
2. Что изучает аналитическая механика?
3. Сформулировать определение понятия «возможные перемещения несвободной механической системы».
4. Сформулировать определение понятия «связи».
5. Сформулировать определение понятия «геометрические связи».
6. Сформулировать определение понятия «стационарные связи».
7. Сформулировать определение понятия «уравнения связей».
8. Сформулировать определение понятия «дифференциальные связи».
9. Сформулировать определение понятия «голономные связи».
10. Сформулировать определение понятия «неголономные связи».
11. Сформулировать определение понятия «нестационарные связи».
12. Сформулировать определение понятия «двусторонние (удерживающие) связи».
13. Сформулировать определение понятия «односторонние (неудерживающие) связи».
14. Сформулировать определение понятия «голономная система».
15. Сформулировать определение понятия «неголономная система».
16. Сформулировать определение понятия «возможное перемещение системы».
17. Сформулировать определение понятия «возможная (элементарная) работа силы».
18. Записать формулу для определения возможной работы силы.
19. Записать формулу для определения возможной работы сил, приложенных к механической системе.
20. Сформулировать определение понятия «идеальные связи».
21. Сформулировать принцип возможных перемещений.
22. Записать формулу, выражающую принцип возможных перемещений, в векторной форме.
23. Записать формулу, выражающую принцип возможных перемещений, в координатной форме.
24. Записать формулу, выражающую принцип возможных скоростей (принцип возможных мощностей).
Дата добавления: 2015-05-30; просмотров: 4741;
