ВОЛНОВЫЕ УРАВНЕНИЯ

Большинство задач электродинамики, в том числе и описание распространения радиоволн, может быть решено с помощью системы уравнений Максвелла в дифференциальной форме:

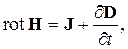
	(2.1)
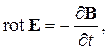
	(2.2)
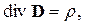
	(2.3)
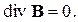
	(2.4)

где	Н	- вектор напряженности магнитного поля, А/м,
	J	- вектор плотности тока, А/м²,
	D	- вектор электрической индукции, Кл/м²;
	Е	- вектор напряженности электрического поля, В/м,
	В	- вектор магнитной индукции, Т,
	ρ	- объемная плотность электрических зарядов, Кл/м³.

Эту систему необходимо решать совместно с материальными уравнениями, учитывающими взаимодействие электромагнитного поля со средой:

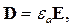
	(2.5)
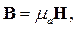
	(2.6)
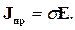
	(2.7)

где	ε_а	- абсолютная диэлектрическая проницаемость среды, Ф/м,
	μ_а	- абсолютная магнитная проницаемость среды, Гн/м,
	J_пр	- вектор плотности тока проводимости, А/м²,
	σ	- электропроводность среды, См/м.

В общем случае точное решение этой системы встречает значительные трудности, поэтому ее необходимо преобразовать к более удобному виду, введя упрощающие предположения. Будем считать, что среда распространения электромагнитных волн является линейной, изотропной и однородной.

<6 7 8910 11 12 >

Дата добавления: 2015-06-12; просмотров: 919;