Комплексное волновое число вводится для описания изменения фазы и затухание волны при распространении в среде с потерями
Подставим эту формулу вместо коэффициента фазы в выражение (1.10). Получим:
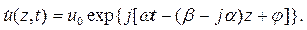
| (1.13) |
Рассмотрим комплексную амплитуду этой волны:
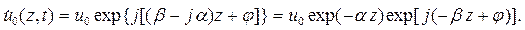
| (1.14) |
По сравнению с формулой (1.11) описание комплексной амплитуды изменилось. Появилась зависимость амплитуды волны от пройденного расстояния, которую описывает exp(-αz). Пройденное расстояние в формуле (1.14) z – величина положительная. Обычно и коэффициент затухания больше нуля. Следовательно, амплитуда волны стала убывающей, а волна – затухающей.
|
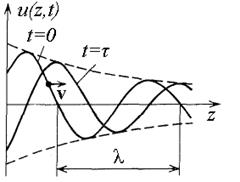
| Рис. 1.5. Мгновенные снимки затухающей волны |
Мгновенные снимки затухающей волны приведены на рис. 1.5. Моменты времени, для которых изображены волны, сдвинуты на τ. За это время волна приходит некоторое расстояние, на котором затухает. Поэтому ее амплитуда убывает по мере возрастания координаты z.
Определяя длину волны, мы записали две формулировки: расстояние, через которое значения периодической функции повторяются и расстояние, проходимое волной за период. Очевидно, что первое определение подходит только для волны в среде без потерь. В среде с потерями с постоянным пространственным периодом будет повторяться только нулевое значение функции. Значит, длину затухающей волны необходимо определять по нулям, как это показано на рис. 1.5.
Все сказанное выше относится к плоской однородной скалярной волне. Плоская она по форме фронта, то есть поверхности постоянной фазы. Волна однородная, так как на поверхности фронта амплитуда ее постоянна. Скалярной эта волна является потому, что процесс описывался скалярной величиной u.
Очевидно, что волна может быть и не плоской и не однородной и не скалярной. Волна будет векторной, если волновой характер имеют компоненты некоторого вектора. Электромагнитные волны всегда описываются векторами.
Рассмотрим гармоническую волну, описываемую следующим соотношением:
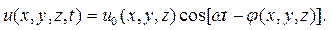
| (1.15) |
И амплитуда u0(x,y,z) и фаза φ(x,y,z) этой волны зависят от всех трех координат. Значит, формула, описывающая поверхность постоянной фазы, то есть волновой фронт, примет следующий вид:
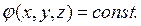
| (1.16) |
В общем случае фронт этой волны не является плоскостью, то есть волна стала неплоской. Если на поверхности фронта амплитуда u0(х, у, z) не постоянна, то волна становится и неоднородной.
Дата добавления: 2015-06-12; просмотров: 1373;
