Стоячей называется волна, узлы и пучности которой неподвижны

Семь мгновенных снимков стоячей волны приведено на рис. 1.4. В первой полуволне, на которой обозначены моменты времени, величина волны максимальна при t = t₁, равна нулю при t = t₄, а минимальна при t = t₇. В следующей полуволне волна максимальна при t = t₇, равна нулю при t = t₄, а минимальна при t = t₁. И так далее. Распределение величины волны повторяется с шагом в один период.

Все сказанное выше о волнах относится к средам без потерь. Но такие среды практически не встречаются. Некоторые потери энергии при распространении любой волны есть всегда. Значит, амплитуда волны должна уменьшаться с расстоянием и это уменьшение необходимо как-то описать. Проще всего это сделать с помощью метода комплексных амплитуд.

Методом комплексных амплитудназывается проведение расчетов с использованием комплексного представления гармонических величин

Комплексный аналог формулы (1.5), описывающей плоскую бегущую волну, имеет вид:

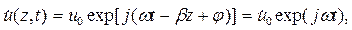
(1.10)

где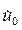

- комплексная амплитуда:

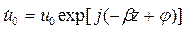
(1.11)

Формула (1.11) описывает комплексную амплитуду волны, распространяющейся в положительном направлении оси z в среде без потерь.

Комплексной амплитудой называется часть математического описания гармонического процесса, не зависящая от времени

Формула (1.5) является действительной частью формулы (1.10).

Обратите внимание на следующий факт. Модуль комплексной амплитуды не зависит от расстояния. Это характерно для любой плоской волны, распространяющейся в среде без потерь.

Для описания затухания электромагнитной волны вводится коэффициент затухания.