ОБЩИЕ СВОЙСТВА ВОЛНОВЫХ ПРОЦЕССОВ

Рис. 1.1. Распространение волны во времени

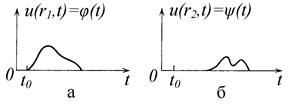
Математическое описание волнового процесса базируется на простых и очевидных соображениях. Пусть в точке А с координатой r₁ физический процесс описывается функцией u(r₁, t) = φ(t), график которой приведен на рис. 1.1, а. Процесс в точке А начинается в момент времени t₀. Теперь рассмотрим точку Б, находящуюся на расстоянии l от точки А. Этой точке соответствует координата r₂. Наш физический процесс не будет наблюдаться в этой точке до тех пор, пока он не будет передан средой.

Через некоторое время мы получим в точке Б процесс, описываемый функцией u(r₂, t) = ψ(t). Зависимость функции u в точке Б от времени приведена на рис. 1.1, б. В общем случен она отличается от зависимости в точке А из-за затухания, искажения при распространении, влияния помех и т.д. Но в простейшем случае в точке Б мы обнаружим лишь запаздывание по времени того процесса, что происходил в точке А. При этом будет выполняться следующее очевидное равенство:

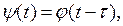
(1.1)

Аргумент функции φ называется фазой волны, а величина τ является сдвигом фазы волны на пути между точками А и Б.

Пусть волна распространяется вдоль оси z. Тогда ее можно описать функцией:

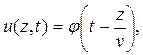
(1.2)

Таким образом, в простейшем случае волна в точках А и Б отличается только сдвигом фазы. Для конкретизации описания процесса распространения волны вводится понятие фронта волны.