Фазовой скоростью называется скорость перемещения фронта волны
Необходимо помнить, что пространственный и временной периоды подобны: за любой из них фаза волны изменяется на 2π.
Для гармонической волны формула (1.2) примет следующий вид:
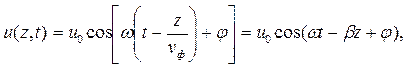
| (1.5) |
| где | u0 | - амплитуда волны; |
| ω | - круговая частота, рад/с; | |
| φ | - начальная фаза волны, рад; | |
| β | - коэффициент фазы, рад/м. |
|
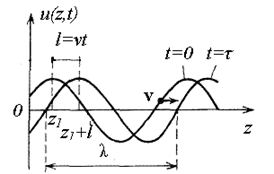
| Рис. 1.3. Мгновенные снимки бегущей волны в среде без потерь |
Эта формула описывает мгновенное значение волны в момент времени t на расстоянии z от источника. Аргумент косинуса называется фазой волны, а введенный здесь параметр β = ω/v – коэффициентом фазы.
Коэффициент фазы показывает, на сколько радиан изменится фаза волны при прохождении одного метра пути
На рис. 1.3 приведены мгновенные снимкибегущей гармонической волныв среде без потерь. Графики построены для двух фиксированных моментов времени 0 и τ. Потерь в среде нет, поэтому амплитуда волны не уменьшается по мере перемещения вдоль оси z. Оба графика - это синусоиды, сдвинутые на расстояние l, которое волна проходит за время τ.
Так как графики построены в зависимости от расстояния, можно выделить пространственный период волны, то есть ее длину λ. Видно, что на пути в одну длину волны фаза изменяется на 2π. Так как волновое число показывает, на сколько радиан изменяется фаза воны на пути в 1 метр, будет выполняться следующее равенство: βλ = 2π. Следовательно, коэффициент фазы можно вычислить двумя способами:
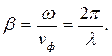
| (1.6) |
Из этого соотношения легко определить фазовую скорость. Получим:
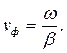
| (1.7) |
Распространение гармонической бегущей волны отображается на рисунках смещением синусоиды со скоростью vф.
Рассмотрим две гармонические волны одинаковой частоты, распространяющиеся навстречу друг другу. Математически этот процесс можно описать следующим образом:
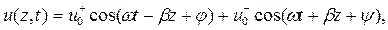
| (1.8) |
| где | 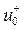
| - амплитуда волны, распространяющейся в положительном направлении оси z; |
| φ | - начальная фаза этой волны; | |
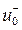
| - амплитуда волны, распространяющейся в отрицательном направлении оси z; | |
| ψ | - начальная фаза этой волны; |
Такой вариант распространения встречается, например, при падении плоской волны на абсолютно отражающую плоскость по направлению нормали.
Прямая и обратная волны складываются и образуют поле достаточно сложной структуры. В простейшем случае, когда амплитуды и начальные фазы волн равны, результирующее поле будет описывать следующее соотношение:
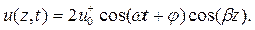
| (1.9) |
Формула (1.9) описывает стоячую волну. Первый косинус формулы (1.9) описывает изменение величины волны во времени, второй – в пространстве, вдоль оси z. Из этой формулы видно, что нули и максимумы стоячей волны неподвижны. Нули стоячей волны называются узлами, а максимумы – пучностями.
Дата добавления: 2015-06-12; просмотров: 855;
