Групповой называется скорость распространения группы волн

Насколько мала должна быть относительная ширина полосы сигнала и как поступать, если сигнал широкополосный, описано в литературе и не является предметом нашего курса. Мы же для первого ознакомления с проблемой рассмотрим распространение сигнала в не поглощающей среде с дисперсией фазовой скорости.

Для того чтобы определить групповую скорость, рассмотрим распространение двух электромагнитных волн одинаковой амплитуды и близких частот. Условие равенства амплитуд волн, составляющих группу, не является обязательным, но существенно упрощает выкладки. Мгновенные значения напряженности электрического поля этих волн можно описать следующими формулами:

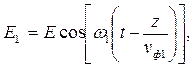
	(7.8)
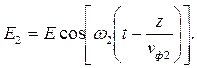
	(7.9)

Вид этих формул несколько необычен из-за того, что коэффициент фазы записан как отношение круговой частоты к фазовой скорости.

Для определения результирующего поля сложим эти волны. Получим:

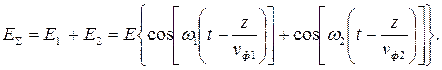
(7.10)

Для дальнейших преобразований воспользуемся следующей формулой из тригонометрии:

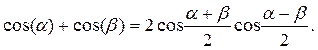
(7.11)

Получим:

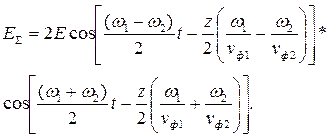
(7.12)

Формула (7.12) показывает, что сумма двух гармонических волн, содержит две составляющих принципиально разных частот. Так как частоты ω₁ и ω₂ близки, половина их разницы в первом сомножителе будет очень мала. А половина суммы во втором сомножителе будет равна средней частоте спектра сигнала. Значит, наш сигнал будет иметь высокочастотную несущую частоту и низкочастотную огибающую. Его мгновенный снимок приведен на рис. 7.1. Он очень похож на амплитудно модулированный сигнал.

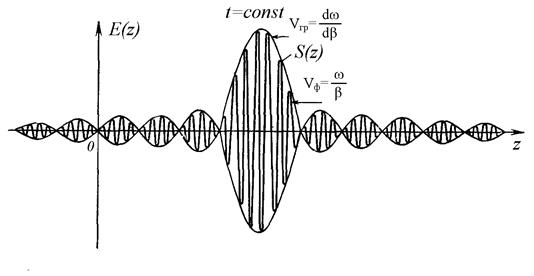
Рис. 7.1. Мгновенный снимок сигнала, состоящего из двух гармонических составляющих

Огибающая сигнала описывается первым сомножителем формулы (7.12), а вы­сокочастотное заполнение - вторым. Максимум энергии сигнала совпадает с максимумом огибающей, так как именно в этом месте амплитуда волны максимальна.

Групповую скорость радиоволны определяют как скорость перемещения огибающей в предположении, что разница частот стремится к нулю. Не вдаваясь в подробности вывода, приведем конечную формулу:

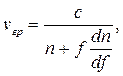
(7.13)

где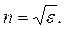

- показатель преломления.