Плоскостью поляризации называется плоскость, образованная вектором напряженности электрического поля и направлением распространения волны

У линейно поляризованной волны положение плоскости поляризации постоянно.

Изменение векторов напряженности электрического и магнитного полей линейно поляризованной волны в пространстве иллюстрирует рис. 6.1. Вектор напряженности электрического поля Е направлен вертикально, а вектор напряженности магнитного поля Н - горизонтально. Направление распространения волны показывает вектор Пойнтинга П. Во времени эта картинка будет перемешаться в направлении распространения с фазовой скоростью.

Электромагнитная волна с линейной поляризацией - это частный случай. В общем случае положение плоскости поляризации изменяется в течение периода. Для понимания этого рассмотрим волновой процесс, который является суммой двух плоских линейно поляризованных волн одинаковой частоты. Вектор напряженности электрического поля первой волны направим вдоль оси х, а второй – вдоль оси у. Следовательно, плоскость поляризации первой волны xz, а второй - yz.

Определим поляризацию получившейся волны. Для этого запишем формулы, описывающие складываемые волны. В фиксированной точке пространства имеем:

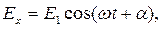
	(6.1)
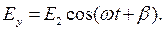
	(6.2)

где	Е1	- амплитуда волны, вектор напряженности электрического поля которой направлен по оси х, В/м;
	α	- фаза этой волны, рад;
	Е2	- амплитуда волны, вектор напряженности электрического поля которой направлен по оси у, В/м;
	β	- фаза этой волны, рад;

Эти волны необходимо сложить. Для упрощения задачи положим, что волны синфазны, то есть α = β. В результате получим:

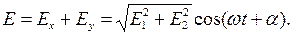
(6.3)

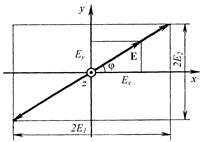
Рис. 6.2. Сложение двух синфазных волн

Иллюстрация процесса сложения приведена на рис. 6.2.Алгоритм сложения следующий. Составляющие поля являются проекциями вектора суммарной волны на оси х и у. Значит, амплитуда суммарного вектора равна корню квадратному из суммы квадратов слагаемых. Конец суммарного вектора будет перемещаться вдоль диагонали прямоугольника, стороны которого равны удвоенным амплитудам складываемых волн 2Е₁ и 2Е₂.

Таким образом, в результате сложения двух линейно поляризованных синфазных волн мы получили новую линейно поляризованную волну. Ориентация вектора напряженности электрического поля суммарной волны постоянна, а в течение периода изменяется только его амплитуда.

Теперь рассмотрим сложение двух волн, сдвинутых по фазе. Величина сдвига фаз принципиального значения не имеет, поэтому для простоты положим его равным π/2. Это позволяет описать слагаемые волны следующими формулами:

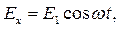
	(6.4)
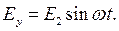
	(6.5)

При записи этих формул начальная фаза опущена, так как она не имеет значения, важен только сдвиг. Сдвиг фазы на π/2 учтен тем, что зависимость от времени напряженности поля второй волны описывается не косинусом, а синусом.

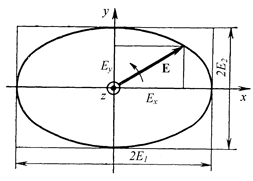
Рис. 6.3. Эллипс поляризации

В данном случае конец вектора напряженности электрического поля за период будет описывать некоторую кривую. Найдем ее уравнение. Для этого правую и левую части формулы (6.4) разделим на Е₁, а правую и левую части формулы (6.5) – на Е₂. Получим:

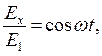
	(6.6)
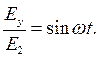
	(6.7)

Далее возведем оба равенства в квадрат и сложим. Получим:

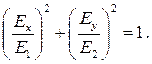
(6.8)

Это - уравнение эллипса. Он изображен на рис. 6.3. Эллипс лежит в плоскости xy и вписан в прямоугольник со сторонами 2E₁ и 2Е₂. Получилось, что за период конец суммарного вектора напряженности электрического поля описывает эллипс. Такую волну называют эллиптически поляризованной.