Плоская электромагнитная волна в среде без потерь переносит только активную мощность

Однако среда без потерь – это идеальный случай. Как только появляются потери, возникает частотная дисперсия фазовой скорости. Это станет очевидно, если обратиться к формуле (5.15):

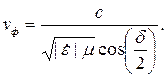
(5.15)

В явном виде частотная зависимость фазовой скорости в этой формуле не прослеживается. Но все-таки она есть. В формуле (5.15) используются модуль комплексной относительной диэлектрической проницаемости и угол потерь. Обе эти величины вычисляются через тангенс угла диэлектрических потерь, который и зависит от частоты.

Рассмотрим, как изменится скорость переноса энергии в среде с частотной дисперсией фазовой скорости. Проблема возникает из-за того, что монохроматическая волна не переносит информации, то есть не является сигналом. По определению, ее амплитуда постоянна, а время существования бесконечно. Характеристики поля изменяются во времени по заранее известному постоянному закону, и не могут переносить информацию.

Реальный электромагнитный процесс никогда не бывает одночастотным. Как только начинается излучение, волна перестает быть монохроматической. В ней, кроме колебания основной частоты, появляются и колебания других частот. Спектр сигнала еще более расширяется после прекращения излучения. На практике для передачи или извлечения информации чаще всего используются различные импульсы, а импульс любой формы и длительности характеризуются спектром частот. Значит, необходимо рассмотреть распространение не монохроматической волны.

Обратимся еще раз к формуле (7.7). Если ε и μ не зависят от частоты, то фазовая скорость и скорость переноса энергии любой спектральной компоненты сигнала одинаковы. В этом случае все компоненты волны приходят в точку приема одновременно, и сигнал на приеме сохранит свою форму.

Если нельзя не учитывать зависимость фазовой скорости волны от частоты, ситуация усложняется. В этом случае имеет место быть частотная дисперсия фазовой скорости.

При распространении сигнала в среде с дисперсией его спектральные составляющие распространяются с разной скоростью и достигают приемника не одновременно. Из-за этого форма сигнала искажается, причем на разных расстояниях фазовые соотношения между спектральными составляющими будут различны. Поэтому результаты сложения компонент сигнала будут зависеть от расстояния. Если эти искажения малы, ими можно пренебречь. Если нет – их необходимо учитывать.

Распространение не монохроматического сигнала в общем случае нельзя рассматривать как одну волну. Каждой спектральной составляющей будет соответствовать своя волна, распространяющаяся со своей фазовой скоростью. Для описания распространения не монохроматического сигнала в среде с частотной дисперсией фазовой скорости вводят понятие группы волн.

Группой волн называется не монохроматический волновой процесс при малой относительной ширине полосы сигнала

Можно полагать, что группа волн распространяется как одно целое. Однако скорость ее распространения отличается от фазовой и называется групповой скоростью.