Решение. Запишем формулу, выражающую принцип Даламбера для механической системы в векторном виде:

Запишем формулу, выражающую принцип Даламбера для механической системы в векторном виде:

Σ 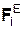+ Σ + ΣФ_i = 0,

где Σ 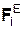– геометрическая сумма активных сил; Σ – геометрическая сумма реакций внешних связей, наложенных на механическую систему; ΣФ_i – геометрическая сумма сил инерции.

Согласно этому принципу на механическую систему действуют активные силы G₁, G₂, реакции Y_О, Z_О внешней связи и силы инерции Ф₁, Ф₂. Применительно к рассматриваемой задаче принцип Даламбера выражается формулой

G₁ + G₂ + Y_О + Z_О + Ф₁ + Ф₂ = 0.

Покажем эти силы на рис. 5.41. Силы G₁, G₂ поместим в центрах С₁, С₂ масс тел 1 и 2.

Используя исходные данные задачи, запишем формулы для определения модулей активных сил и сил инерции:

G₁ = m₁·g; G₂ = m₂·g.

Так как механическая система вращается с постоянной угловой скоростью , то угловое ускорение 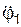= 0 и, следовательно, модули a_С1, a_С2 ускорений центров С₁, С₂ масс тел 1 и 2 соответственно равны:

a_С1 = 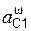= ( )²·0,5·l sin(α);

a_С2 = 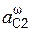= ( )²·l sin(α),

где 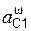, 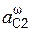– модули центростремительных ускорений центров масс тел рассматриваемой механической системы.

Тогда имеем:

Φ₁ = m₁·a_С1 = m₁· 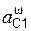= m₁·(( )²·0,5·l sin(α));

Φ₂ = m₁·a_С2 = m₁· 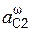= m₂·(( )²·l sin(α)).

Сила инерции Ф₁ тела 1 приложена в точке D на расстоянии ОD = 2·l/3, так как эпюра распределения элементарных сил инерции тела 1 имеет форму треугольника.

Согласно рис. 5.43 на рассматриваемую конструкцию действует плоская произвольная система сил (G₁, G₂, Y_О, Z_О, Ф₁, Ф₂). Принцип Даламбера в этих условиях выражается системой трех уравнений.

Σ + Σ + Σ 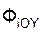= 0; (1)

Σ + Σ + Σ 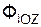= 0; (2)

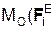Σ 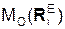) + Σ + Σ 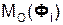= 0, (3)

где 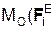Σ 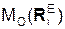), Σ , Σ 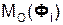– суммы моментов соответственно активных сил, реакций внешних связей и сил инерции относительно точки О.

Преобразуем последние уравнения к следующему виду:

Y_О – Φ₁ – Φ₂ = 0; (1^I)

– G₁ – G₂ + Z_О = 0; (2^I)

G₁·0,5·l·sin(α) + G₂·l·sin(α) – Φ₁·(2·l/3)·cos(α) – Φ₂·l·cos(α) = 0. (3^I)

При использовании условий задачи эти уравнения принимают вид:

Y_О – m₁·(( )²·0,5·l sin(α)) – m₂·(( )²·l·sin(α)); (1^II)

– m₁·g – m₂·g + Z_О = 0; (2^II)

m₁·g·0,5·l·sin(α) + m₂·g·l·sin(α) –

– m₁·(( )²·0,5·l·sin(α))·(2·l/3)·cos(α) –

– m₂·(( )²·l·sin(α))·l·cos(α) = 0. (3^II)

В трёх уравнениях (1^II), (2^II), (3^II) содержатся три неизвестные величины: Y_О, Z_О, . Решим эти уравнения.

Из уравнения (3^II) имеем

= =

= =

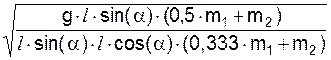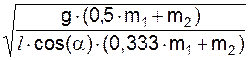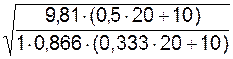= = 3,686 рад/с.

Из уравнения (2^II) следует, что

Z_О = g·(m₁ + m₂) = 9,81·(20 + 10) = 294,300 H.

Из уравнения (1^II) получим

Y_О = ( )²·l ·sin(α)·(0,5·m₁+ m₂) =

= 3,686²·1·0,5·(0,5·20 + 10) = 135,939 )H.

Таким образом, ответы на вопросы (Y_О = ?, Z_О = ?), поставленные в курсовом задании Д 5, получены.