И механической системы
5.6.1. Принцип Даламбера для несвободной
материальной точки
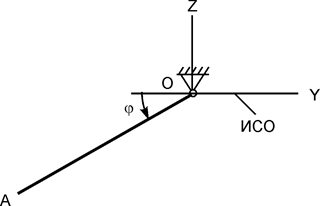
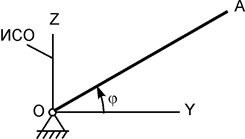
Рассмотрим движение несвободной материальной точки под действием активных сил  и реакций
и реакций 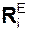 внешних связей в инерциальной системе отсчёта OXYZ (рис. 5.34).
внешних связей в инерциальной системе отсчёта OXYZ (рис. 5.34).
Следует отметить, что на точку могут действовать несколько активных сил и реакций внешних связей. Однако на рис. 5.34 показаны только по одной из этих сил.
Основное уравнение динамики точки имеет вид
m·a = Σ  + Σ
+ Σ  .
.
Перенесём произведение m·a из левой части рассматриваемого уравнения в правую его часть:
Σ  + Σ
+ Σ  – m·a = 0.
– m·a = 0.
Введём условное обозначение Ф = – m·a. Назовём Ф силой инерции материальной точки.

Сила инерции материальной точки – величина, равная произведению массы точки на её ускорение и направленная противоположно этому ускорению.
Как вектор сила инерции Ф имеет размерность [Н] и характеризуется тремя элементами: точкой приложения (приложена в точке, движение которой рассматривается); направлением (направлена в сторону, противоположную направлению ускорения a); модулем Ф, который определяется по формуле Ф = m·a.
Исходя из изложенного выше, последнее векторное равенство представим в следующем виде:
Σ  + Σ
+ Σ  + Ф = 0.
+ Ф = 0.
Это векторное уравнение и выражает принцип Даламбера для несвободной материальной точки.
В любой момент времени для движущейся несвободной материальной точки геометрическая сумма активных сил, реакций внешних связей и силы инерции равна нулю.
По существу, основное уравнение динамики точки (m·a = Σ  + Σ
+ Σ  ) преобразовано к другому виду (Σ
) преобразовано к другому виду (Σ  + Σ
+ Σ  + Ф = 0), который широко применяется в статике механических систем.
+ Ф = 0), который широко применяется в статике механических систем.
Поскольку силовой многоугольник, построенный на векторах активных сил  , реакций
, реакций  внешних связей и силы инерции Ф замкнут, то суммы проекций этих сил на координатные оси системы отсчёта OXYZ равны нулю. Спроецируем векторное равенство (Σ
внешних связей и силы инерции Ф замкнут, то суммы проекций этих сил на координатные оси системы отсчёта OXYZ равны нулю. Спроецируем векторное равенство (Σ  + Σ
+ Σ  + Ф = 0) на координатные оси инерциальной системы отсчёта и получим следующие равенства:
+ Ф = 0) на координатные оси инерциальной системы отсчёта и получим следующие равенства:
Σ  + Σ
+ Σ  + ФОХ = 0;
+ ФОХ = 0;
Σ  + Σ
+ Σ  + ФOY = 0;
+ ФOY = 0;
Σ  + Σ
+ Σ  + ФOZ = 0.
+ ФOZ = 0.
Сумма проекций активных сил, реакций внешних связей и силы инерции на координатные оси инерциальной системы отсчёта равна нулю.
Последние уравнения зачастую называют уравнениями динамического равновесия материальной точки, в отличие от уравнений (Σ  + Σ
+ Σ  = 0; Σ
= 0; Σ  + Σ
+ Σ  = 0; Σ
= 0; Σ  + Σ
+ Σ  = 0) статического равновесия.
= 0) статического равновесия.
В действительности сила инерции материальной точки приложена не к ней, а к телу, взаимодействующему с рассматриваемой точкой. Приложение силы инерции к точке является лишь условным приёмом, сводящим задачу динамики по форме решения к задаче статики.
Благодаря простоте, принцип Даламбера получил широкое применение во многих инженерных дисциплинах. В ряде случаев он обеспечивает наиболее простое и удобное решение задач динамики.
5.6.2. Принцип Даламбера для несвободной
механической системы

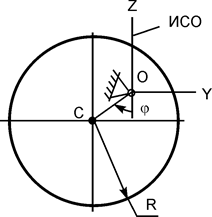
Рассмотрим движение материальной точки Ci несвободной неизменяемой механической системы под действием активной силы  , реакции
, реакции  внешней связи и внутренней силы
внешней связи и внутренней силы  в инерциальной системе отсчёта OXYZ со скоростью VCi и ускорением aCi (рис. 5.35).
в инерциальной системе отсчёта OXYZ со скоростью VCi и ускорением aCi (рис. 5.35).
Применим принцип Даламбера для каждой точки Ci неизменяемой механической системы.
 +
+  +
+  + Фi = 0,
+ Фi = 0,
где Φi = – m·aCi – сила инерции материальной точки Ci механической системы.
Просуммируем составленные уравнения и получим выражение
Σ  + Σ
+ Σ  + Σ
+ Σ  + ΣФi = 0.
+ ΣФi = 0.
Поскольку механическая система неизменяемая, то геометрическая сумма реакций  внутренних связей равна нулю (Σ
внутренних связей равна нулю (Σ 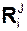 = 0). Тогда получим
= 0). Тогда получим
Σ  + Σ
+ Σ  + ΣФi = 0.
+ ΣФi = 0.
В любой момент времени для неизменяемой механической системы геометрическая сумма активных сил, реакций внешних связей и сил инерции равна нулю.
Это и есть принцип Даламбера для неизменяемой механической системы.
Этот принцип зачастую записывают в следующем виде:
F* + R* + Φ* = 0,
где F* = Σ  – главный вектор активных сил; R* = Σ
– главный вектор активных сил; R* = Σ  – главный вектор реакций внешних связей; Φ* = ΣФi – главный вектор сил инерции.
– главный вектор реакций внешних связей; Φ* = ΣФi – главный вектор сил инерции.
В любой момент времени для неизменяемой механической системы геометрическая сумма главных векторов активных сил, реакций внешних связей и сил инерции равна нулю.
Как правило, векторное равенство F* + R* + Φ* = 0, выражающее принцип Даламбера, применяют при рассмотрении поступательного движения твёрдого тела.
Используя метод Пуансо для каждой материальной точки механической системы, приведём произвольно направленные в пространстве активные силы  , реакции
, реакции  внешних связей и силы инерции Фi к центру масс механической системы (рис. 5.36).
внешних связей и силы инерции Фi к центру масс механической системы (рис. 5.36).

Необходимо отметить, что метод Пуансо справедлив для любой произвольной точки, но, как правило, в инженерной практике за такую точку принимают центр масс твёрдого тела или механической системы.
Согласно методу Пуансо система активных сил  , реакций
, реакций  внешних связей и сил инерции Фi эквивалентна системе сил (F*, R*, Φ*) и системе присоединённых пар сил с векторными моментами
внешних связей и сил инерции Фi эквивалентна системе сил (F*, R*, Φ*) и системе присоединённых пар сил с векторными моментами 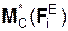 ,
, 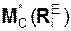 ,
, 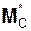 (Фi), где
(Фi), где 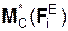 = Σ
= Σ 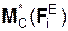 – главный момент активных сил относительно центра масс;
– главный момент активных сил относительно центра масс; 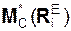 = Σ
= Σ 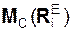 – главный момент реакций внешних связей относительно центра масс;
– главный момент реакций внешних связей относительно центра масс; 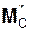 (Фi) = Σ
(Фi) = Σ 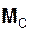 (Фi) – главный момент сил инерции относительно центра масс.
(Фi) – главный момент сил инерции относительно центра масс.
С использованием условных обозначений: F*, R*, Φ*, 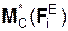 ,
, 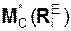 ,
, 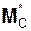 (Фi) принцип Даламбера преобразуется в совокупность двух векторных выражений:
(Фi) принцип Даламбера преобразуется в совокупность двух векторных выражений:
F* + R*+ Φ*= 0;
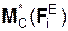 +
+ 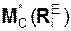 +
+ 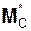 (Фi) = 0.
(Фi) = 0.
В любой момент времени для движущейся неизменяемой механической системы геометрические суммы главных векторов и главных моментов активных сил, реакций внешних связей и сил инерции относительно произвольного центра (как правило, относительно центра масс) равны нулю.
Спроецируем последние векторные равенства на координатные оси системы отсчёта OXYZ и получим шесть уравнений, выражающих принцип Даламбера в скалярной форме:
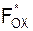 +
+  +
+ 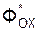 = 0;
= 0;
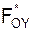 +
+ 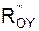 +
+  = 0;
= 0;
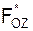 +
+  +
+ 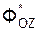 = 0;
= 0;
 = 0;
= 0;
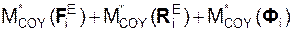 = 0;
= 0;
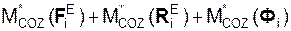 = 0,
= 0,
где 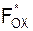 ,
, 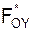 ,
, 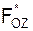 – проекции главного вектора активных сил на координатные оси;
– проекции главного вектора активных сил на координатные оси;  ,
, 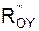 ,
,  – проекции главного вектора реакций внешних связей на координатные оси;
– проекции главного вектора реакций внешних связей на координатные оси; 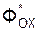 ,
,  ,
, 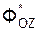 – проекции главного вектора сил инерции на координатные оси;
– проекции главного вектора сил инерции на координатные оси;  ,
, 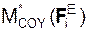 ,
,  – проекции главного момента активных сил на координатные оси;
– проекции главного момента активных сил на координатные оси; 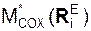 ,
, 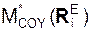 ,
, 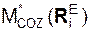 – проекции главного момента реакций внешних связей на координатные оси;
– проекции главного момента реакций внешних связей на координатные оси; 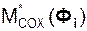 ,
,  ,
, 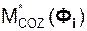 – проекции главного момента сил инерции на координатные оси.
– проекции главного момента сил инерции на координатные оси.
В любой момент времени для движущейся неизменяемой механической системы суммы проекций главных векторов активных сил, реакций внешних связей и сил инерции, а также суммы проекций главных моментов активных сил, реакций внешних связей и сил инерции относительно произвольного центра на координатные оси инерциальной системы отсчёта равны нулю.
Как правило, в инженерной практике силы не приводят в одну точку и, следовательно, такими понятиями, как главные векторы сил и главные моменты сил относительно произвольной точки не пользуются, а применяют силы, приложенные в различных точках механической системы. В этом случае принцип Даламбера выражается следующими уравнениями:
Σ  + Σ
+ Σ  + Σ
+ Σ 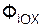 = 0;
= 0;
Σ  + Σ
+ Σ  + Σ
+ Σ 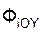 = 0;
= 0;
Σ  + Σ
+ Σ  + Σ
+ Σ 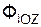 = 0;
= 0;
Σ  + Σ
+ Σ 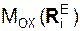 + Σ
+ Σ  = 0;
= 0;
 Σ
Σ 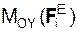 + Σ
+ Σ 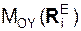 + Σ
+ Σ 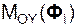 = 0;
= 0;
Σ 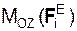 + Σ
+ Σ 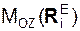 + Σ
+ Σ 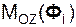 = 0,
= 0,
где Σ  , Σ
, Σ  , Σ
, Σ  – суммы проекций активных сил на координатные оси; Σ
– суммы проекций активных сил на координатные оси; Σ  , Σ
, Σ  , Σ
, Σ  – суммы проекций реакций внешних связей на координатные оси; Σ
– суммы проекций реакций внешних связей на координатные оси; Σ 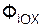 , Σ
, Σ 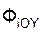 , Σ
, Σ 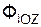 – суммы проекций сил инерции на координатные оси; Σ
– суммы проекций сил инерции на координатные оси; Σ  , Σ
, Σ 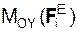 , Σ
, Σ 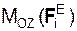 – суммы моментов активных сил относительно координатных осей; Σ
– суммы моментов активных сил относительно координатных осей; Σ 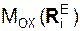 , Σ
, Σ 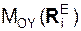 , Σ
, Σ 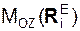 – суммы моментов реакций внешних связей относительно координатных осей; Σ
– суммы моментов реакций внешних связей относительно координатных осей; Σ  , Σ
, Σ 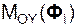 , Σ
, Σ 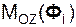 – суммы моментов сил инерции относительно координатных осей.
– суммы моментов сил инерции относительно координатных осей.
В любой момент времени для движущейся неизменяемой механической системы суммы проекций активных сил, реакций внешних связей и сил инерции на координатные оси, а также суммы моментов активных сил, реакций внешних связей и сил инерции относительно координатных осей равны нулю.
Последние математические выражения применяются для механических систем, расположенных в трёхмерном пространстве. Для плоских систем используют двумерное пространство. В таком пространстве принцип Даламбера выражается следующими уравнениями:
Σ  + Σ
+ Σ  + Σ
+ Σ 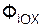 = 0;
= 0;
Σ  + Σ
+ Σ  + Σ
+ Σ 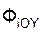 = 0;
= 0;
Σ 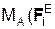 ) + Σ
) + Σ 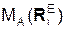 + Σ
+ Σ  = 0,
= 0,
где Σ 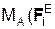 ), Σ
), Σ 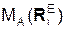 , Σ
, Σ  – суммы моментов соответственно активных сил, реакций внешних связей и сил инерции относительно произвольной точки А.
– суммы моментов соответственно активных сил, реакций внешних связей и сил инерции относительно произвольной точки А.
В любой момент времени для движущейся неизменяемой механической системы суммы проекций активных сил, реакций внешних связей и сил инерции на координатные оси, а также сумма моментов активных сил, реакций внешних связей и сил инерции относительно произвольной точки равны нулю.
В инженерной практике, как правило, принцип Даламбера применяют для определения реакций внешних связей, наложенных на механическую систему.
5.6.3. Приведение сил инерции точек твёрдого
тела к простейшему виду
В данном учебно-методическом пособии рассматриваются неизменяемые механические системы, в которые входят тела, осуществляющие следующие виды движений: поступательное, вращательное, плоскопараллельное.
При поступательном движении силы инерции материальных точек приводятся к главному вектору Ф* сил инерции, который прикладывается в центре масс твёрдого тела (рис. 5.37) и определяется по формуле

Ф* = – m·aС.
Согласно рис. 5.37 главный вектор сил инерции Ф* направлен в сторону, противоположную ускорению aС. Модуль главного вектора сил инерции определяется по формуле Ф* = m·aС.

Рассмотрим вращательное движение твёрдого тела относительно оси ОХ, которая не проходит через его центр масс (рис. 5.38).
Согласно положениям кинематики имеем векторное равенство
aС = 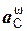 +
+ 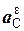 ,
,
где aС – ускорение центра масс; 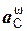 – центростремительное ускорение центра масс;
– центростремительное ускорение центра масс; 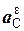 – вращательное ускорение центра масс.
– вращательное ускорение центра масс.
В рассматриваемом случае силы инерции материальных точек тела приводятся к главному вектору Ф* сил инерции и главному векторному моменту 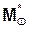 , определяемым по формулам:
, определяемым по формулам:
Ф* = Фω + Фε;
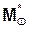 = – JCX1·
= – JCX1· 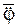 ,
,
где Фω = – m· 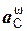 – центробежная сила инерции; Фε = – m·
– центробежная сила инерции; Фε = – m· 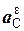 – вращательная сила инерции; JCX1 – момент инерции тела относительно оси СХ1, проходящей через центр масс;
– вращательная сила инерции; JCX1 – момент инерции тела относительно оси СХ1, проходящей через центр масс; 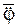 – вектор углового ускорения.
– вектор углового ускорения.
Направления сил инерции Фω, Фε показаны на рис. 5.36. Модули составляющих Фω, Фε главного вектора Ф* сил инерции и приведённого момента 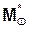 сил инерции определяют по формулам:
сил инерции определяют по формулам:
Фω = m·(( 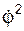 )·CO); Фε = m·(I
)·CO); Фε = m·(I  I·CO);
I·CO); 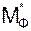 = МΦ = JCX1·I
= МΦ = JCX1·I 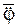 I,
I,
где m,  , I
, I 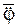 I – соответственно масса, угловая скорость и модуль углового ускорения
I – соответственно масса, угловая скорость и модуль углового ускорения 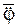 тела; СО – расстояние от центра масс до оси вращения.
тела; СО – расстояние от центра масс до оси вращения.
В инженерной практике наиболее часто используется вариант, в котором центробежная и вращательная силы инерции прикладываются в центре масс (см. рис. 5.38). Этот вариант и рекомендуется для дальнейшего использования как основной вариант.
Для общего ознакомления приведём и другие варианты приложения сил инерции.
Рассмотрим вариант вращательного движения твёрдого тела, при котором силы инерции Фω, Фε прикладываются на оси вращения (рис. 5.39).
В этом случае модули искомых инерционных нагрузок определяются по формулам:
Фω = m·( 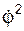 ·CO); Фε = m·(I
·CO); Фε = m·(I  I·CO);
I·CO); 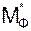 = МΦ = JОX·I
= МΦ = JОX·I 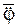 I,
I,
где JОХ – момент инерции тела относительно оси вращения.


Рассмотрим вариант вращательного движения твёрдого тела (рис. 5.40), при котором: Фω = m·( 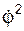 ·CO); Фε = m·(I
·CO); Фε = m·(I  I·CO);
I·CO); 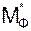 = МΦ = 0.
= МΦ = 0.
В этом случае центробежную и вращательную силы инерции прикладывают в точке О1, а расстояние ОО1 определяют по формуле
ОО1 = JОХ/(m·CO),
где JОХ – момент инерции тела относительно оси вращения.

В инженерной практике широкое распространение имеет вариант, при котором ось вращения тела проходит через его центр масс (рис. 5.41).
В рассматриваемом случае силы инерции материальных точек твёрдого тела приводятся к моменту МФ сил инерции.
МФ = JСХ· I 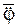 I.
I.

Определим и покажем на рис. 5.42 главный вектор Ф* сил инерции и момент МФ сил инерции при плоскопараллельном движении твёрдого тела.
При таком движении твёрдого тела имеем:
Ф* = m·ac; МФ = JCZ·I 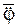 I,
I,
где JCZ – момент инерции тела относительно оси CZ вращения, проходящей через центр масс.
Для закрепления изложенного материала студентам рекомендуется выполнить курсовое задание Д 5.
5.6.4. Варианты курсового задания Д 5
«Применение принципа Даламбера
к определению реакций связей»
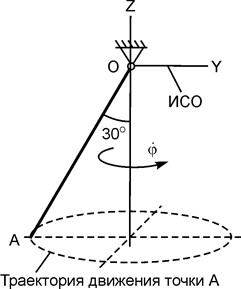
Определить реакции внешних связей механической системы: в заданном положении для вариантов 4, 5, 10, 19, 21 – 30; в момент времени t1 для вариантов 1, 8, 9, 20; в тот момент времени, когда угол поворота имеет значение φ1, для вариантов 2, 3, 6, 7.
На расчётных схемах плоскость OXY (AXY) горизонтальна, плоскость OYZ (AYZ) вертикальна. Расчётные схемы механизмов и необходимые для решения данные приведены в табл. 5.3, в которой  – угловая скорость; φ0,
– угловая скорость; φ0, 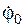 – значения угла поворота и угловой скорости в начальный момент времени.
– значения угла поворота и угловой скорости в начальный момент времени.
Примечания:
Для варианта 17. Радиус инерции ротора 2 двигателя 3; iС2Х2 = 0,10 м.
Для варианта 21. Радиус инерции ротора 2 двигателя 3 ; iС2Х2 = 0,12 м.
Для варианта 25. Радиус инерции шкива 3 iС3Х3 = 0,18 м.
Для варианта 26. Радиус инерции шкива 3 iС3Х3 = 0,22 м.
Для варианта 27. Радиус инерции шкива 3 iС3Х3 = 0,15 м.
Для варианта 28. Радиус инерции шкива 3 iС3Х3 = 0,15 м.
Вращающиеся тела, для которых не задан радиус инерции, рассматривать как тонкие однородные стержни или сплошные однородные диски (варианты 5, 6 – 9, 12, 16, 20, 22). На схемах вариантов 1, 8, 9, 16, 17, 20 – 22 указаны внешние моменты М.
Таблица 5.3
| Номер варианта | Расчётная схема механизма | Исходные данные |
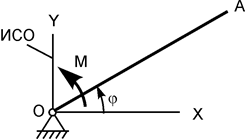
|
m = 20 кг;
l = 0,60 м;
М = 1,0 Н·м;
t1 = 10 c;
φ0 = 0о;
 = 0 рад/с = 0 рад/с
| |
|
m = 25 кг;
l = 0,50 м;
φ1 = 60о;
φ0 = 0о;
 = 0 рад/с = 0 рад/с
| |
|
m = 40 кг;
l = 0,80 м;
φ1 = 60о;
φ0 = 0о;
 = 6,3 рад/с = 6,3 рад/с
|
Продолжение табл. 5.3
| m = 20 кг; l = 0,80 м | |
|
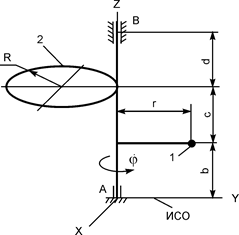
m1 = 30 кг;
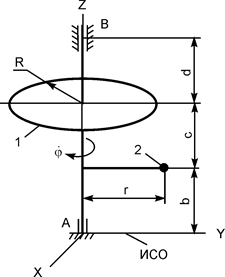
m2 = 1,5 кг;
r = 0,60 м;
R = 0,50 м;
b = 0,30 м;
с = 0,40 м;
d = 0,30 м;
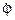 = 6 рад/с = 6 рад/с
| |

|
m = 40 кг;
R = 0,30 м;
φ1 = 30о;
φ0 = 0о;
 = 0 рад/с = 0 рад/с
|
Продолжение табл. 5.3
|
m = 20 кг;
R = 0,25 м;
φ1 = 60о;
φ0 = 0о;
ОС = R/2;
 = 5,5 рад/с = 5,5 рад/с
| |
|
m = 50 кг;
R = 0,30 м;
М = 4,0 Н·м;
t1 = 5 c;
φ0 = 0о;
 = 0 рад/с = 0 рад/с
| |
| m1 = 20 кг; m2 = 5 кг; r = 0,60 м; R = 0,50 м; b = 0,30 м; с = 0,25 м; d = 0,30 м; M = 10t Н·м; t1 = 2 c |
Продолжение табл. 5.3
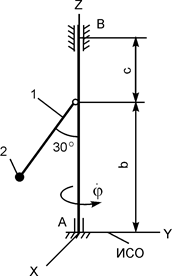
|
m1 = 12 кг;
m2 = 5 кг;
l1 = 0,25 м;
b = 0,40 м;
с = 0,20 м;
 = 10 рад/с = 10 рад/с
| |
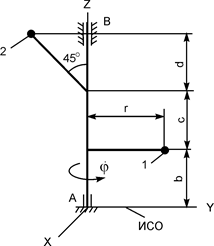
|
m1 = 10 кг;
m2 = 6 кг;
r = 0,25 м;
b = 0,30 м;
с = 0,40 м;
d = 0,35 м;
 = 10 рад/с = 10 рад/с
| |
|
m1 = 10 кг;
m2 = 6 кг;
R = 0,25 м;
r = 0,20 м;
b = 0,30 м;
с = 0,50 м;
d = 0,35 м;
 = 10 рад/с = 10 рад/с
|
Продолжение табл. 5.3

|
m1 = 10 кг;
m2 = 6 кг;
b = 0,50 м;
с = 0,20 м;
 = 10 рад/с = 10 рад/с
| |

|
m = 10 кг;
b = 0,80 м;
с = 0,20 м;
 = 10 рад/с = 10 рад/с
| |

|
m1 = 10 кг;
m2 = 20 кг;
b = 0,30 м;
с = 0,80 м;
d = 0,35 м;
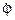 = 10 рад/с = 10 рад/с
|
Продолжение табл. 5.3
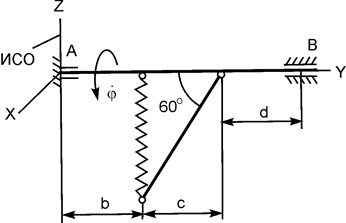
| m1 = 80 кг; m2 = 20 кг; m3 = 0,4m1; R3 = 0,10 м; М = 100 Н·м | |
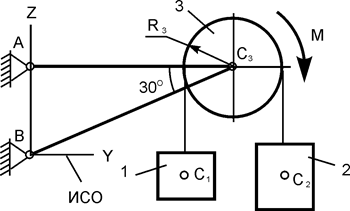
| m1 = 10 кг; m2 = 20 кг; m3 = 10 кг; M = 30 Н·м; R2 = 0,2 м; b = 0,30 м; с = 0,80 м | |
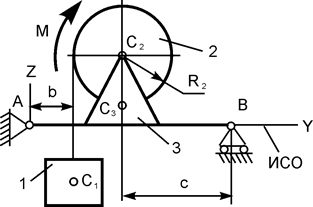
|
m = 10 кг;
b = 0,30 м;
с = 0,20 м;
d = 0,35 м;
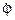 = 10 рад/с = 10 рад/с
|
Продолжение табл. 5.3
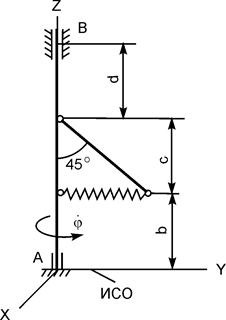
|
m = 12 кг;
b = 0,30 м;
с = 0,25 м;
d = 0,35 м;
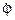 = 8 рад/с = 8 рад/с
| |

|
m = 40 кг;
R = 0,30 м;
M = 3,0 H·м;
OC = R/2;
t1 = 4 c;
φ0 = 0о;
 = 8 рад/с = 8 рад/с
| |
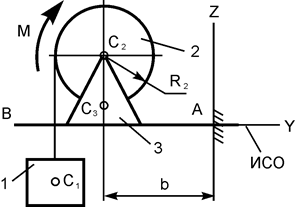
| m1 = 100 кг; m2 = 40 кг; m3 = 15 кг; M = 124 H·м; R2 = 0,2 м; b = 0,30 м |
Продолжение табл. 5.3
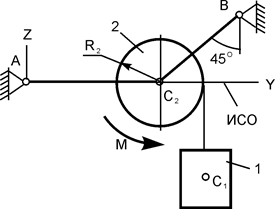
| m1 = 80 кг; m2 = 20 кг; R2 = 0,10 м; М = 120 Н·м | |

|
m1 = 10 кг;
m2 = 25 кг;
b = 0,30 м;
с = 0,50 м;
d = 0,35 м;
 = 10 рад/с = 10 рад/с
| |
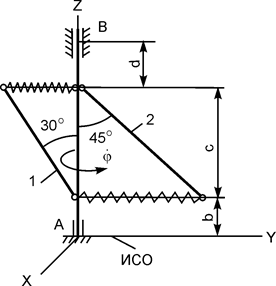
|
m1 = 10 кг;
m2 = 25 кг;
b = 0,20 м;
с = 0,50 м;
d = 0,30 м;
 = 12 рад/с = 12 рад/с
|
Продолжение табл. 5.3
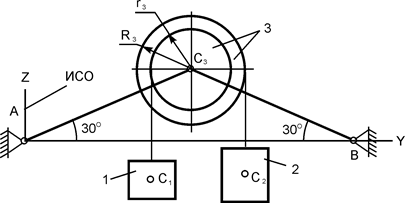
| m1 = 10 кг; m2 = 25 кг; m3 = 20 кг; R3 = 0,30 м; r3 = 0,20 м | |
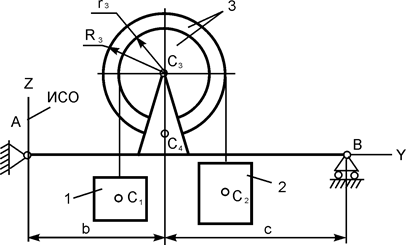
| m1 = 80 кг; m2 = 20 кг; m3 = 20 кг; m4 = 20 кг; R3 = 0,30 м; r3 = 0,20 м; b = 0,20 м; c = 0,30 м | |
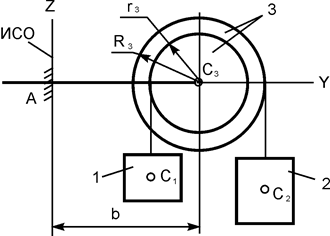
| m1 = 50 кг; m2 = 20 кг; m3 = 20 кг; R3 = 0,25 м; r3 = 0,15 м; b = 0,20 м |
Окончание табл. 5.3
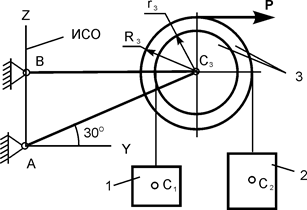
| m1 = 30 кг; m2 = 15 кг; m3 = 15 кг; P = 300 H; R3 = 0,25 м; r3 = 0,15 м | |
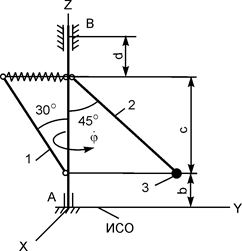
|
m1 = 10 кг;
m2 = 25 кг;
m3 = 25 кг;
b = 0,20 м;
с = 0,15 м;
d = 0,25 м;
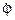 = 8 рад/с = 8 рад/с
| |
|
m1 = 10 кг;
m2 = 25 кг;
m3 = 20 кг;
m4 = 15 кг;
b = 0,50 м;
с = 0,35 м;
d = 0,15 м
 = 16 рад/с = 16 рад/с
|
5.6.5. Пример выполнения курсового задания Д 5
В курсовом задании Д 5 требуется определить реакции внешних связей, наложенных на механическую систему в следующих случаях: в произвольный момент времени; в фиксированный момент времени t1; в тот момент времени, когда угол поворота тела равен значению φ1.
Рассмотрим последовательно эти случаи.
Дата добавления: 2015-05-30; просмотров: 1796;
