Внимание!

Независимо от знака момента M_OZ(t), заданного в исходных данных задачи, на рис. 5.14 направление этого момента рекомендуется показывать против хода часовой стрелки. Это позволяет решать задачу в общем виде и получать частные решения при любых исходных данных.

Так как активный момент M_OZ(t) зависит от времени, то очевидно, что при его действии на механическую систему будет изменяться её угловая скорость .

В принятых условных обозначениях теорема об изменении кинетического момента механической системы записывается в виде

dL_O1Z1/dt = ΣM_O1Z1( ) + ΣM_O1Z1( ).

Определим производную по времени от кинетического момента механической системы относительно оси вращения.

dL_O1Z1/dt = d(4,2· )/dt = 4,2·d /dt.

Сумма моментов активных нагрузок, приложенных к механической системе, относительно оси вращения равна

ΣM_O1Z1( ) = M_OZ(t) = – 6,3· .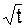

Сумма моментов реакций внешних связей относительно оси вращения равна нулю (ΣM_O1Z1( ) = 0).

В этих условиях теорема об изменении кинетического момента механической системы относительно оси вращения приобретает вид дифференциального уравнения:

4,2·d /dt = – 6,3· 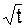= – 6,3·t^0,5.

Проинтегрируем это уравнение и решим его:

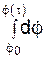= – 1,5 ;

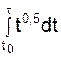(t) – 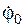= – 1,5(τ^0,5+1/1,5) = – τ^0,5+1 = – ;

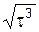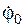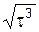(t) = – = 5 – 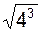= 5 – 8 = – 3 рад/с.

Таким образом, при приложении активного момента M_OZ = – 6,3· 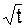к механической системе её угловая скорость за промежуток времени τ = 4 с изменится с начального значения 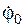= 5 рад/с до значения (t) = – 3 рад/с.

Ответ на один из вопросов ( (t) = ?) курсового задания получен.

Третий этап.

Рассмотрим движение механической системы в момент времени Т, когда на неё действуют только активные силы G₁, G₂ (силы тяжести тел системы); реакции X_O1, Y_O1, Z_O1 в точке О₁ подпятника и реакции X_D, Y_D цилиндрического шарнира в точке D (рис. 5.15).

Поскольку материальная точка К совершает сложное движение (перемещается по вращающемуся телу 1), то необходимо рассмотреть это движение в подвижной (ПСО) и неподвижной инерциальной (ИСО) системах отсчёта. Так как ПСО закреплена на теле 1, то она совершает вращательное движение.

Из курса кинематики известно, что абсолютная скорость точки в сложном движении равна

V = V_r + V_e,

где V_r – относительная скорость; V_e – переносная скорость.

Определим абсолютную скорость V_С2 точки К.

В нашем случае траектория относительного движения точки – траектория её движения по телу 1. Такой траекторией является дуга АВ окружности радиусом R. По условию задания уравнение относительного движения точки (OK = (5·π·R/6)·t₁) известно. Зафиксируем положение точки К на траектории относительного движения в момент времени Т центральным углом α.

OK(T) = (5·π·R/6)·T = (5·π·R/6)·1 = (5·π·R/6).

α = OK(T)/R = (5·π·R/6)/R = 5·π/6 рад.

В градусной мере α = 150^о. На рис. 5.15 покажем траекторию переносного движения точки К. Эта траектория есть окружность, расположенная в горизонтальной плоскости. Центр окружности находится на оси вращения. Радиус окружности определим по формуле

r = b – R·sin(π – α) = b – b·sin(α) =

= b·(1 – sin(α)) = b·(1 – 0,5) = 0,5·b.

Абсолютную скорость V_С2 центра масс тела 2 (абсолютную скорость точки К) определим по формуле

V_С2 = V_С2r + V_С2e,

где V_С2r – относительная скорость; V_С2e – переносная скорость.

По заданному уравнению относительного движения (ОК = S = S(t₁)) определим проекцию V_С2r относительной скорости точки на касательную к траектории её движения.

V_С2r = dS/dt₁ = d((5·π·R/6)·t₁)/dt₁ = 5·π·R/6 = const > 0.

Поскольку dS/dt₁ > 0, то относительная скорость V_С2r направлена в сторону увеличения дуговой координаты ОК = S (см. рис. 5.15). Необходимо отметить, что вектор скорости V_С2r лежит в плоскости рисунка.

Модуль V_С2e переносной скорости V_С2e центра масс тела 2 определим по формуле

V_С2e = r·I (T)I = 0,5·b·I (T)I,

где I (T)I – модуль угловой скорости тела 1 в момент времени Т.

Вектор V_С2e переносной скорости направлен перпендикулярно плоскости рис. 5.15 (параллельно оси О₁Х₁).

Абсолютное количество движения m₂·V_С2 тела 2 находим по формуле

m₂·V_С2 = m₂·(V_С2r + V_С2e) = m₂·V_С2r + m₂·V_С2e,

где m₂·V_С2r, m₂·V_С2e – соответственно относительное и переносное количества движения.

Векторы m₂·V_С2r, m₂·V_С2e покажем на рис. 5.15.

Запишем теорему об изменении кинетического момента механической системы для рассматриваемого этапа расчета:

dL_O1Z1/dt₁ = ΣM_O1Z1( ) + ΣM_O1Z1( ).

Поскольку сумма моментов активных сил относительно оси O₁Z₁ вращения равна нулю (ΣM_O1Z1( ) = 0) и сумма моментов реакций внешних связей относительно той же оси также равна нулю (ΣM_O1Z1( ) = 0), то, следовательно, имеем dL_O1Z1/dt₁ = 0. Отсюда следует, что L_O1Z1 = const, т. е. при движении механической системы её кинетический момент относительно оси не изменяется. Имеет место случай сохранения кинетического момента механической системы относительно оси O₁Z₁ её вращения. Исходя из этого, справедливо утверждение

L_O1Z1(τ) = L_O1Z1(Т),

где L_O1Z1(τ), L_O1Z1(Т) – кинетические моменты механической системы в расчётные моменты времени τ и Т.

В начальный момент времени (t₁₀ = 0) имеем: угловая скорость прямоугольной пластины (t) = – 3 рад/с; векторы количеств движения m₂·V_C2r, m₂·V_C2e направлены так, как это показано на рис. 5.15.

Кинетический момент L_O1Z1(t₁₀ = 0) механической системы в начальный момент времени определим по формуле

L_O1Z1(t₁₀ = 0) = 4,2· (t).

Кинетический момент L_O1Z1(Т) механической системы в момент времени Т равен

L_O1Z1(Т) = L_O1Z1(1,T) + L_O1Z1(2,T),

где L_O1Z1(1,T), L_O1Z1(2,T) – соответственно кинетические моменты тел 1 и 2 относительно оси вращения в момент времени Т.

L_O1Z1(1,T) = 2,4· (Т).

L_O1Z1(2,T) = m₂·V_С2e·r = (m₂·( (Т)·r))·r = m₂· (Т)·r² =

= m₂· (T)·(0,5·b)² = 5· (Т)·(0,5·0,6)² = 0,45· (Т).

Тогда

L_O1Z1(Т) = 2,4· (Т) + 0,45· (Т) = 2,85· (Т).

Так как кинетический момент механической системы относительно оси вращения постоянен, то

L_O1Z1(t₁₀ = 0) = 4,2 (t) = L_O1Z1(Т) = 2,85· (Т).

Отсюда

(Т) = (4,2 (t))/2,85 = (4,2·(– 3))/2,85 = – 4,427 рад/с.

По сравнению с исходным положением расчёта третьего этапа, когда угловая скорость пластины была равна (t) = – 3 рад/с, в конце расчёта её угловая скорость уменьшилась до значения (Т) = – 4,427 рад/с. Модуль угловой скорости увеличился на 1,427 рад/с. Произошло это потому, что центр масс механической системы сместился к оси вращения. Очевидно, что угловая скорость пластины достигнет максимального значения в момент времени, когда точка К будет находиться на оси вращения.

Таким образом, ответ на другой вопрос ( (Т) = ?) курсового задания получен.

Вопросы и задания для самоконтроля

1. Сформулировать определение понятия «момент количества движения точки относительно произвольного центра».

2. Сформулировать определение понятия «плечо вектора количества движения точки относительно произвольного центра».

3. Сформулировать определение понятия «момент количества движения точки относительно оси».

4. Записать формулы для определения моментов количества движения точки относительно координатных осей.

5. Записать в векторной форме формулу, выражающую теорему об изменении момента количества движения материальной точки.

6. Записать в скалярном виде формулу, выражающую теорему об изменении момента количества движения материальной точки.

7. Сформулировать определение понятия «центральная сила».

8. Сформулировать определение понятия «кинетический момент механической системы относительно центра».

9. Сформулировать определение понятия «кинетический момент механической системы относительно оси».

10. Записать в скалярном виде формулы, выражающие теорему об изменении кинетического момента механической системы относительно координатных осей.

11. Сформулировать следствия из теоремы об изменении кинетического момента механической системы относительно координатных осей.