Решение. Такое допущение обосновано тем, что тело совершает поступательное движение и, следовательно, уравнения его движения такие же
 |
1. Рассмотрим движение тела на участке АВ в заданной системе отсчёта АX1Y1, приняв его за материальную точку (рис. 1.16).
Такое допущение обосновано тем, что тело совершает поступательное движение и, следовательно, уравнения его движения такие же, как и у точки.
2. Изобразим точку в системе отсчёта АX1Y1 в произвольный момент времени t. При этом её координата Х1 = f(t) > 0 и точка движется в сторону возрастания этой координаты ускоренно. Следовательно, ускорение a имеет такое же направление, как и скорость V.
3. Согласно условию задачи при t0 = 0 начальная координата Х10 = Х1А = 0 и проекция начальной скорости 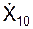 = VA.
= VA.
4. К точке приложим активную силу G – силу тяжести. Так как опорная поверхность точки шероховатая, то имеем две реакции: N – нормальная реакция; Ftr – сила трения скольжения. Силу Ftr направляют в сторону, противоположную направлению скорости V. Из курса статики известно, что модули силы трения и нормальной реакции связывает соотношение Ftr = f·N.
5. Запишем основное уравнение динамики точки.
m·a = ΣFiЕ + ΣRiЕ = G+ N + Ftr.
Спроецировав это векторное выражение на координатные оси системы отсчёта АX1Y1, получим дифференциальные уравнения движения точки:
m· 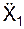 = G·sin(α) – Ftr; (1)
= G·sin(α) – Ftr; (1)
m· 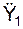 = G·cos(α) – N, (2)
= G·cos(α) – N, (2)
где 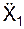 ,
, 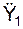 – проекции ускорения a на координатные оси.
– проекции ускорения a на координатные оси.
Поскольку вектор a на ось AY1 не проецируется, то из уравнения (2) имеем N = G·cos(α) = m·g·cos(α). Отсюда имеем
Ftr = f·N = f·m·g·cos(α).
Анализируя последнее равенство, сделаем вывод о том, что реакции N и Ftr не зависят от того, в каком кинематическом состоянии (покоя или движения) находится точка.
С учетом изложенного уравнение (1) приводится к виду
m· 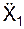 = G·sin(α) – Ftr = G·sin(α) – f·N·cos(α) =
= G·sin(α) – Ftr = G·sin(α) – f·N·cos(α) =
= m·g·sin(α) – f·m·g·cos(α) = m·g·(sin(α) – f·cos(α)). (1I)
Упростим последнее выражение.
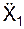 = g·(sin(α) – f·cos(α)). (1II)
= g·(sin(α) – f·cos(α)). (1II)
6. Дважды проинтегрируем последнее уравнение.
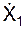 = g·(sin(α) – f·cos(α))·t + C1;
= g·(sin(α) – f·cos(α))·t + C1;
X1 = g·(sin(α) – f·cos(α))·t2/2 + C1·t + C2,
где С1, С2 – постоянные интегрирования.
7. Определим постоянные С1, С2 подстановкой в последние уравнения начальных условий движения. При t0 = 0 имеем:
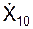 = VA = g·(sin(α) – f·cos(α))·t0 + C1;
= VA = g·(sin(α) – f·cos(α))·t0 + C1;
X10= Х1A = 0 = g·(sin(α) – f·cos(α))·(t0)2/2 + C1·t0 + C2.
Отсюда С1 = VA; С2 = 0. Окончательно имеем:
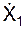 = g·(sin(α) – f·cos(α))·t + VA;
= g·(sin(α) – f·cos(α))·t + VA;
X1 = g·(sin(α) – f·cos(α))·t2/2 + VA·t,
где X1, 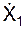 – соответственно текущие координата точки и проекция её скорости на координатную ось АХ1.
– соответственно текущие координата точки и проекция её скорости на координатную ось АХ1.
Последние выражения справедливы для любого значения времени, пока точка движется по участку АВ. В момент времени τ движущееся тело находится в точке В участка АВ. Исходя из этого, получим систему двух уравнений.
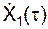 = VB = g·(sin(α) – f·cos(α))·τ + VA;
= VB = g·(sin(α) – f·cos(α))·τ + VA;
Х1(τ) = l = g·(sin(α) – f·cos(α))·τ2/2 + VA·τ.
Эта система уравнений содержит неизвестные τ и VB. Поскольку число уравнений равно числу неизвестных величин, то такую систему уравнений решают стандартными приёмами и определяют VB и τ. После определенияVB и τ рассматривают движение материальной точки на участке ВС её траектории в системе отсчёта ВХY (см. рис. 1.15).
Если последнюю систему уравнений решить нельзя (число неизвестных превышает число уравнений равновесия), то так же переходят к рассмотрению движения точки на участке ВС в системе отсчёта ВXY.
8. Рассмотрим движение точки на участке ВС в заданной системе отсчёта ВXY.
 |
9. Изобразим точку на траектории её движения в произвольный момент времени (рис. 1.17).
10. Определим начальные условия движения точки на участке ВС. Согласно рис. 1.17 имеем: Х0 = 0; 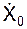 = VB·cos(α); Y0 = 0;
= VB·cos(α); Y0 = 0; 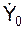 = VB·sin(α).
= VB·sin(α).
11. На точку действует только одна активная сила G – сила тяжести. Реакций связей нет, поскольку сопротивление воздуха не учитывается.
12. Основное уравнение динамики для точки имеет вид
m·a = ΣFiE + ΣRiE = G.
Запишем дифференциальные уравнения движения точки.
m· 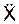 = Σ
= Σ 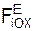 + Σ
+ Σ 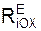 = 0; (3)
= 0; (3)
m· 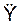 = Σ
= Σ 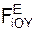 + Σ
+ Σ 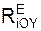 = G = m·g. (4)
= G = m·g. (4)
13. Проинтегрируем последние уравнения. Так как масса точки m ≠ 0, то из уравнения (3) имеем 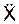 = 0. Отсюда следует, что
= 0. Отсюда следует, что 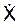 = C3 = const, где
= C3 = const, где 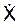 – проекция скорости на координатную ось ВХ; С3 – постоянная интегрирования. Определим С3 по начальным условиям движения. При t0 = 0 имеем
– проекция скорости на координатную ось ВХ; С3 – постоянная интегрирования. Определим С3 по начальным условиям движения. При t0 = 0 имеем 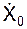 = VB·cos(α) = C3. Так как
= VB·cos(α) = C3. Так как 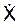 = const, то окончательно получим выражение
= const, то окончательно получим выражение 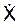 = VB·cos(α). Другими словами, в любой момент времени проекция скорости на координатную ось ВХ постоянна, т. е. не зависит от времени.
= VB·cos(α). Другими словами, в любой момент времени проекция скорости на координатную ось ВХ постоянна, т. е. не зависит от времени.
Проинтегрировав последнее выражение, получим
X = VB·cos(α)·t + C4,
где С4 – постоянная интегрирования.
Определим эту постоянную по начальным условиям движения. При t0 = 0 имеем X0 = 0 = VB·cos(α)·t0 + C4. Отсюда получим С4 = 0. Окончательно текущее значение координаты X точки находят по формуле
X = VB·cos(α)·t.
Дифференциальное уравнение (4) движения точки приведем к виду 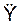 = g. Проинтегрируем это выражение и получим
= g. Проинтегрируем это выражение и получим
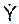 = g·t + C5,
= g·t + C5,
где 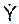 – текущее значение проекции скорости на координатную ось BY; С5 – постоянная интегрирования.
– текущее значение проекции скорости на координатную ось BY; С5 – постоянная интегрирования.
По начальным условиям движения имеем
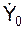 = VB·sin(α) = g·t0 + C5.
= VB·sin(α) = g·t0 + C5.
Отсюда С5 = VB·sin(α). Тогда 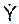 = g·t + VB·sin(α).
= g·t + VB·sin(α).
Проведём интегрирование последнего выражения.
Y = g·t2/2 + VB·sin(α)·t + C6.
Определим постоянную интегрирования С6. При t0 = 0 имеем
Y0 = 0 = g·(t0)2/2 + VB·sin(α)·t0 + C6.
Тогда С6 = 0.
Текущее значение координаты y находят по формуле
Y = g·t2/2 + VB·sin(α)·t.
Таким образом, получаем выражения для определения текущих значений координат X, Y и проекций 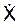 ,
, 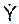 скорости точки при её движении по траектории ВС. В момент времени Т, когда тело находится в точке С траектории его движения (см. рис. 1.17), эти выражения приобретают следующий вид:
скорости точки при её движении по траектории ВС. В момент времени Т, когда тело находится в точке С траектории его движения (см. рис. 1.17), эти выражения приобретают следующий вид:
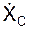 = VB·cos(α);
= VB·cos(α); 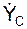 = g·Т + VB·sin(α);
= g·Т + VB·sin(α);
d = VB·cos(α)·T; h = g·T2/2 + VB·sin(α)·T,
где 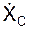 ,
, 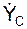 – проекции скорости VC на координатные оси; d, h – координаты точки С в системе отсчёта ВXY.
– проекции скорости VC на координатные оси; d, h – координаты точки С в системе отсчёта ВXY.
По условию задачи требуется определить модуль скорости тела в точке С траектории его движения. Для этого используется формула 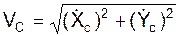 .
.
Таким образом, для определения неизвестных величин необходимо совместно решить следующую систему уравнений:
VB = g·(sin(α) – f·cos(α))·τ + VA;
l = g·(sin(α) – f·cos(α))·τ2/2 + VAτ;
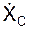 = VB·cos(α);
= VB·cos(α); 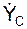 = g·Т + VB·sin(α);
= g·Т + VB·sin(α);
d = VB·cos(α)·T; h = g·T2/2 + VB·sin(α)·T;
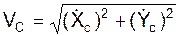 .
.
В этой системе уравнений неизвестными величинами являются: VB, τ, d, T, 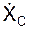 ,
, 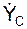 , VC.
, VC.
Таким образом, имеем семь уравнений, содержащих семь неизвестных.
Для координации вектора VC скорости тела в точке С пространства рекомендуется определить величину угла β, составленного направлением этой скорости с положительным направлением отсчета координаты Х по формулам:
cos(VC, i) = 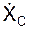 /VC; β = arcos(
/VC; β = arcos( 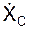 /VC).
/VC).
Результаты проведённых расчётов сводят в таблицу.
Вопросы и задания для самоконтроля
1. Сформулировать первый закон динамики (закон инерции).
2. Сформулировать второй закон динамики (закон пропорциональности силы и ускорения).
3. Сформулировать третий закон динамики (закон равенства действия и противодействия).
4. Сформулировать четвёртый закон динамики (закон независимости действия сил).
5. Сформулировать определение понятия «инерциальная система отсчёта».
6. Записать основное уравнение динамики несвободной материальной точки.
7. Записать дифференциальные уравнения движения несвободной материальной точки в декартовой системе отсчёта.
8. Записать дифференциальные уравнения движения несвободной материальной точки в естественных координатных осях.
9. Сформулировать суть первой задачи динамики.
10. Сформулировать суть второй задачи динамики.
11. Как определяются постоянные интегрирования при решении второй задачи динамики?
Дата добавления: 2015-05-30; просмотров: 1323;
