Точки в декартовой системе отсчёта. Во второй (обратной) задаче динамики по известным силам, действующим на материальную точку, и начальным условиям её движения требуется определить уравнения
Во второй (обратной) задаче динамики по известным силам, действующим на материальную точку, и начальным условиям её движения требуется определить уравнения движения точки: X = f1(t), Y = f2(t), Z = f3(t), а также её положение, скорость и ускорение в момент времени t1. Эта задача имеет большое практическое значение и в общем случае является более сложной по сравнению с первой задачей динамики.
Алгоритм решения второй задачи динамики содержит следующие действия.
1. В механической системе выделяют материальную точку, движение которой рассматривают.
2. Выбирают инерциальную систему отсчёта ОXYZ. Начало системы отсчёта располагают в точке тела, по отношению к которому рассматривают движение выделенной из механической системы материальной точки.
3. В системе отсчёта ОXYZ точку изображают в произвольный момент времени таким образом, чтобы она имела положительные координаты и двигалась в сторону их увеличения ускоренно.
4. По исходным данным задачи определяют и изображают на рисунке начальные условия движения (X0, Y0, Z0, 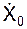 ,
, 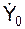 ,
, 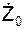 ).
).
5. К точке прикладывают активные (задаваемые) силы FiЕ.
6. Согласно аксиоме связей эти связи отбрасывают и их действие заменяют соответствующими реакциями RiЕ.
7. Записывают дифференциальные уравнения движения точки:
m· 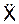 = Σ
= Σ 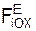 + Σ
+ Σ 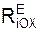 ;
;
m· 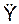 = Σ
= Σ 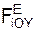 + Σ
+ Σ 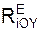 ;
;
m· 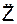 = Σ
= Σ 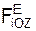 + Σ
+ Σ 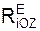 ,
,
где 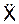 ,
, 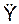 ,
, 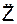 – проекции ускорения a на координатные оси; Σ
– проекции ускорения a на координатные оси; Σ 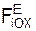 , Σ
, Σ 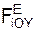 , Σ
, Σ 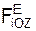 – суммы проекций активных сил FiE на соответствующие координатные оси ИСО; Σ
– суммы проекций активных сил FiE на соответствующие координатные оси ИСО; Σ 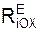 , Σ
, Σ 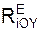 , Σ
, Σ 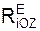 – суммы проекций реакций RiE внешних связей на оси ИСО.
– суммы проекций реакций RiE внешних связей на оси ИСО.
8. Дифференциальные уравнения движения точки дважды интегрируют. При интегрировании каждого дифференциального уравнения появляются две постоянные и, следовательно, при интегрировании трёх дифференциальных уравнений будем иметь шесть постоянных: С1 – С6.
9. Определяют значения постоянных Ci интегрирования по начальным условиям движения: значения трёх координат точки и проекции её скорости на три оси в некоторый момент времени, обычно (но не обязательно) в начальный момент времени (t0 = 0). Как правило, в условиях задачи задают следующие начальные условия движения: X0, Y0, Z0, 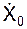 ,
, 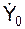 ,
, 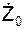 . Эти данные подставляют в уравнения, представляющие общие решения дифференциальных уравнений движения точки, и определяют постоянные интегрирования Ci.
. Эти данные подставляют в уравнения, представляющие общие решения дифференциальных уравнений движения точки, и определяют постоянные интегрирования Ci.
10. Подставляя найденные значения постоянных интегрирования Ci в общие решения дифференциальных уравнений движения точки, получают уравнения её движения в виде:
X = f1(t, X0, Y0, Z0, 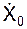 ,
, 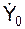 ,
, 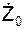 );
);
Y = f2(t, X0, Y0, Z0, 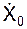 ,
, 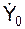 ,
, 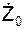 );
);
Z = f3(t, X0, Y0, Z0, 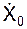 ,
, 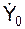 ,
, 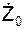 ).
).
Анализ последних уравнений показывает, что под действием одной и той же системы сил, приложенных к точке, она может совершать целый класс движений, зависящих от начальных условий.
При составлении дифференциальных уравнений движения материальной точки за расчётный начальный момент времени (t0 = 0) обычно принимают момент начала движения точки под действием заданных сил, для которого известны как положение точки, так и её скорость.
Введением начальной скорости точки учитывают влияние на её движение сил, действующих на точку до того момента времени, который принят за начальный момент.
Дифференциальные уравнения движения точки описывают её движение до тех пор, пока на точку действует заданная система сил.
Если в какой-то момент времени система сил, действующих на точку, изменится, то для описания последующего движения точки составляют новые дифференциальные уравнения. Начальными условиями нового движения точки будут её положение и скорость в конце предшествующего движения.
11. По уравнениям движения точки X = f1(t), Y = f2(t), Z = f3(t) определяют её кинематические характеристики для заданного момента времени t1. Как правило, результаты расчётов сводят в таблицу и при необходимости иллюстрируют рисунками.
Алгоритм решения вторых задач динамики в естественных координатных осях по существу не отличается от вышеприведенного алгоритма. Здесь он не рассмотрен, так как студенты заочной и дистанционной форм обучения не выполняют курсовых заданий на эту тему.
Для закрепления изложенного теоретического материала рекомендуется выполнить курсовое задание Д 1.
Варианты курсового задания Д 1
Дата добавления: 2015-05-30; просмотров: 975;
