Интегрирование дифференциальных уравнений
движения материальной точки,
находящейся под действием постоянных сил»
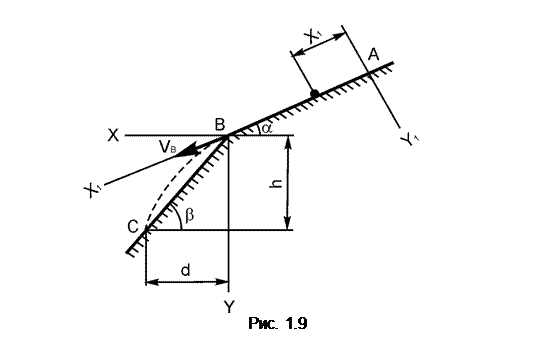 |
Варианты 1 – 5 (рис 1.9)
Тело совершает поступательное движение из точки А по участку АВ (длиной l) наклонной плоскости, составляющей угол α с горизонтом, в течение τ секунд. Его начальная скорость VA. Коэффициент трения скольжения тела по плоскости равен f.
В точке В тело покидает плоскость со скоростью VB и попадает со скоростью VC в точку С участка BC, наклоненного под углом β к горизонту, находясь в воздухе Т секунд.
При решении задачи тело принять за материальную точку; сопротивление воздуха не учитывать.
Вариант 1. Дано: α = 30о; VA = 0; f = 0,2; l = 10 м; β = 60о. Определить τ и h.
Вариант 2. Дано: α = 15о; VA = 2 м/с; f = 0,2; h = 4 м; β = 45о. Определить l и уравнение траектории точки на участке ВС (Y = f(X)).
Вариант 3. Дано: α = 30о; VA = 2,5 м/с; f ≠ 0; l = 8 м; d = 10 м; β = 60о. Определить VB и τ.
Вариант 4. Дано: VA = 0 м/с; τ= 2 с; l = 9,8 м; β = 60о; f = 0. Определить α и T.
Вариант 5. Дано: α = 30о; VA = 0 м/с; τ= 3 с; l = 9,8 м; β = 45о. Определить f и VC.
Варианты 6 – 10 (рис. 1.10)
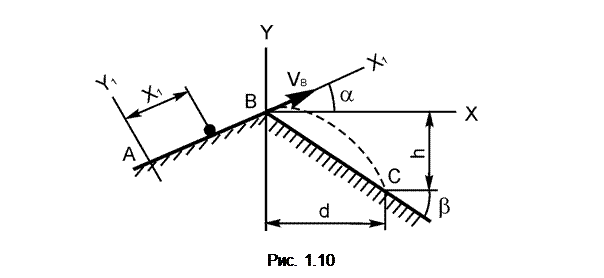
Тело совершает поступательное движение и подходит к точке А участка АВ, наклоненного под углом α к горизонту и имеющего длину l со скоростью VA. Коэффициент трения скольжения на участке АВ равен f. Тело от точки А до точки В движется τ секунд; в точке В со скоростью VB оно покидает участок АВ. Через Т секунд тело приземляется со скоростью VC в точке С участка ВС, составляющем угол β с горизонтом.
При решении задачи тело принять за материальную точку и не учитывать сопротивление воздуха.
Вариант 6. Дано: α = 20о; f = 0,1; τ= 0,2 с; h = 40 м; β = 30о. Определить l и VC.
Вариант 7. Дано: α = 15о; f = 0,1; VA = 16 м/с; l = 5 м; β = 45о. Определить VB и T.
Вариант 8. Дано: VA = 21 м/с; f = 0; τ= 0,3 с; VB = 20 м/с; β = 60о. Определить α и d.
Вариант 9. Дано: α = 15о; τ= 0,3 с; f = 0,1; h = 30 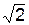 м; β = 45о. Определить VB и VA.
м; β = 45о. Определить VB и VA.
Вариант 10. Дано: α = 15о; f = 0; VA = 12 м/с; d = 50 м; β = 60о. Определить τ и уравнение траектории тела (Y = f(X) = ?) в системе отсчёта XВY.
Варианты 11 – 15 (рис. 1.11)
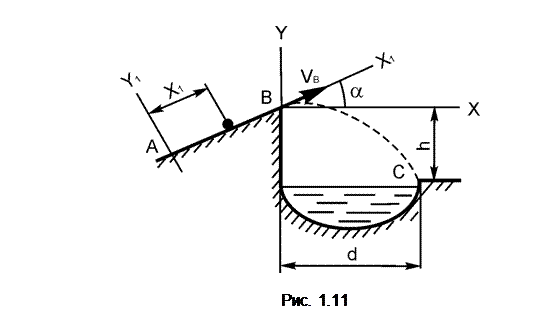 |
Имея в точке А скорость VA, тело поднимается τ секунд по участку АВ длиной l, составляющему с горизонтом угол α. При постоянной на всем участке АВ движущей силе Р тело в точке В приобретает скорость VB и перелетает через ров шириной d, находясь в воздухе Т секунд и приземляясь в точке С со скоростью VC. Масса тела равна m.
При решении задачи считать тело материальной точкой и не учитывать силы сопротивления движению.
Вариант 11. Дано: α = 30о; Р ≠ 0; l = 40 м; VA = 0; VB = 4,5 м/с; d = 3 м. Определить τ и h.
Вариант 12. Дано: α = 30о; Р = 0; l = 40 м; VB = 4,5 м/с; h = 1,5 м. Определить VA и d.
Вариант 13. Дано: α = 30о; m = 400 кг; VA = 0; τ= 20 с; d = 3 м; h = 1,5 м. Определить Р и l.
Вариант 14. Дано: α = 30о; m = 400 кг; Р = 2,2 кН; VA = 0; l =40 м; d = 5 м. Определить VB и VС.
Вариант 15. Дано: α = 30о; VA = 0; Р = 2 кН; l = 50 м; h = 2м; d = 4 м. Определить Т и m.
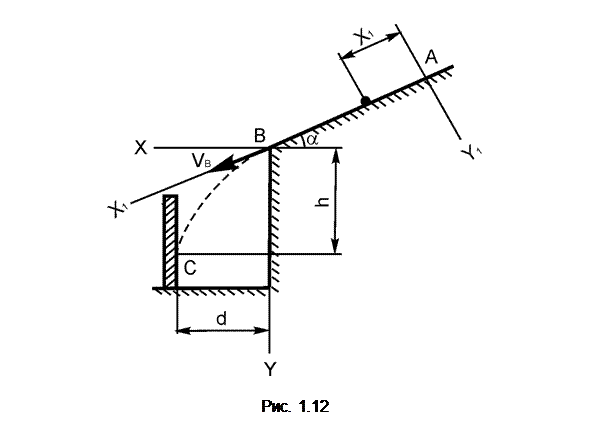 |
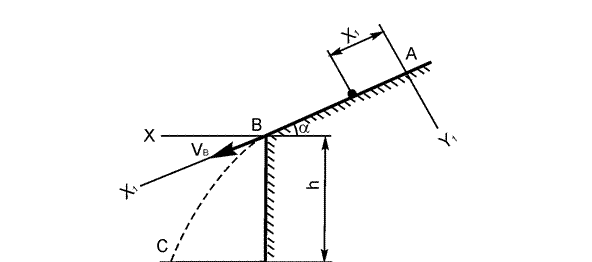
Варианты 16 – 20 (рис. 1.12)
Тело скользит в течение τ секунд по участку АВ откоса, составляющему угол α с горизонтом и имеющему длину l. Его начальная скорость VA. Коэффициент трения скольжения тела по откосу равен f. Имея в точке В скорость VB , тело через Т секунд ударяется в точке С о защитную стену.
При решении задачи принять тело за материальную точку; сопротивление воздуха не учитывать.
Вариант 16. Дано: α = 30о; VA = 1 м/с; l = 3 м; f = 0,2; d = 2,5 м. Определить T и h.
Вариант 17. Дано: α = 45о; l = 6 м; VB = 2·VA; τ= 1 c; h = 6 м. Определить d и f.
Вариант 18. Дано: α = 30о; l = 2 м; VA = 0; f = 0,1; d = 3 м. Определить h и τ.
Вариант 19. Дано: α = 15о; l = 3 м; VB = 3 м/с; f ≠ 0; τ= 1,5 c; d = 2 м. Определить VA и h.
Вариант 20. Дано: α = 45о; VA = 0; f = 0,3; d = 2 м; h = 4м. Определить l и τ.
Варианты 21 – 25 (рис. 1.13)
 |
Тело движется из точки А по участку АВ (длиной l) наклонной плоскости, составляющей угол α с горизонтом. Его начальная скорость VA. Коэффициент трения скольжения равен f. Через τ секунд тело в точке В со скоростью VB покидает наклонную плоскость и падает на горизонтальную плоскость в точку С со скоростью VC; при этом оно находится в воздухе Т секунд.
При решении задачи принять тело за материальную точку и не учитывать сопротивление воздуха.
Вариант 21. Дано: α = 30о; f = 0,1; VA = 1 м/с; τ= 1,5 c; h = 10 м. Определить VB и d.
Вариант 22. Дано: VA = 0; α = 45о; l = 10 м; τ= 2 c. Определить f и уравнение траектории (Y = f(X) = ?) на участке ВС в системе отсчёта XВY.
Вариант 23. Дано: f = 0; VA = 0; l = 9,81 м; τ= 2 с; h = 20 м. Определить α и Т.
Вариант 24. Дано:VA = 0; α = 30о; f = 0,2; l = 10 м; d = 12 м. Определить τ и h.
Вариант 25. Дано: VA = 0; α = 30о; f = 0,2; l = 6 м; h = 4,5 м. Определить VC и τ.
Варианты 26 – 30 (рис. 1.14)
 |
Имея в точке А скорость VA, тело движется по горизонтальному участку АВ длиной l в течение τ секунд. Коэффициент трения скольжения по плоскости равен f. Со скоростью VB тело в точке В покидает плоскость и попадает в точку С со скоростью VC, находясь в воздухе Т секунд.
При решении задачи принять тело за материальную точку; сопротивление воздуха не учитывать.
Вариант 26. Дано: VA = 7 м/с; f = 0,2; l = 8 м; h = 20 м. Определить VC и d.
Вариант 27. Дано: VA = 4 м/с; f = 0,1; τ= 2 c; d = 2 м. Определить VB и h.
Вариант 28. Дано: VB = 3 м/с; f = 0,3; l = 3 м; h = 5 м. Определить VA и Т.
Вариант 29. Дано: VA = 3 м/с; VB = 1 м/с; l = 2,5 м; h = 20 м. Определить f и d.
Вариант 30. Дано: f = 0,25; l = 4 м; d = 3 м; h = 5 м. Определить VA и τ.
Дата добавления: 2015-05-30; просмотров: 2072;
