Точки в естественных координатных осях. В первой задаче динамики точки известно уравнение S = f(t) движения точки в естественных координатных осях
В первой задаче динамики точки известно уравнение S = f(t) движения точки в естественных координатных осях. Могут быть заданы начальные условия движения, к которым относятся дуговая координата S0 и скорость V0 в момент времени t0 = 0. При естественном способе задания движения точки известно следующее: вид траектории движения; начало отсчёта дуговой координаты S; положительное (+) и отрицательное (–) направления отсчёта дуговой координаты.
Алгоритм решения первых задач динамики в естественных координатных осях представляет собой следующую совокупность действий исполнителя.
1. Изображается известная траектория движения точки. На этой траектории наносятся начало отсчёта (О), положительное (+) и отрицательное (–) направления отсчёта дуговой координаты S.
2. Точка изображается на траектории движения в произвольный момент времени. При этом точка имеет координату S > 0 и движется в сторону её увеличения ускоренно.
3. В эту точку помещается начало координат ПСО, которая представляет собой совокупность трёх взаимно перпендикулярных осей: касательная, главная нормаль, бинормаль. При этом единичный вектор τ всегда направлен в сторону увеличения дуговой координаты S. Единичный вектор n направлен к центру кривизны траектории движения точки.
4. По данным задачи определяют и изображают на рисунке начальные условия движения (S0, V0).
5. К точке прикладывают активные силы FiE и реакции RiE внешних связей.
6. Записывают дифференциальные уравнения движения точки, которые имеют следующий вид:
m· 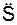 = Σ
= Σ 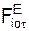 + Σ
+ Σ 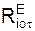 ;
;
m· 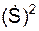 /ρ = Σ
/ρ = Σ 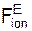 + Σ
+ Σ 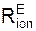 ;
;
Σ 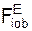 + Σ
+ Σ 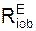 = 0.
= 0.
7. По заданному уравнению движения S = f(t) определяют проекцию 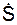 скорости и проекцию
скорости и проекцию 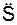 ускорения точки на касательную.
ускорения точки на касательную.
8. Определённые проекции 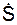 ,
, 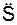 подставляют в дифференциальные уравнения движения точки.
подставляют в дифференциальные уравнения движения точки.
9. Определяют проекции Poτ, Pon равнодействующей активных сил FiE и реакций RiE внешних связей на координатные оси ПСО. Для этого необходимо решить следующие уравнения:
Poτ = m· 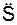 = Σ
= Σ 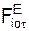 + Σ
+ Σ 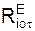 ; (1)
; (1)
Pon = m· 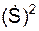 /ρ = Σ
/ρ = Σ 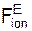 + Σ
+ Σ 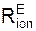 ; (2)
; (2)
Σ 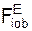 + Σ
+ Σ 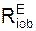 = 0. (3)
= 0. (3)
10. Определяют модуль Р равнодействующей активных сил FiE и реакций RiE внешних связей, действующих на точку.
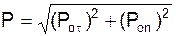 .
.
11. Для ориентации вектора Р в пространстве определяют направляющие косинусы.
cos(P, τ) = Pоτ/P; cos(P, n) = Pоn/P.
12. По величине значений направляющих косинусов находят значения углов, составленных направлениями координатных осей ПСО и силой Р.
13. Равнодействующую Р активных сил FiЕ и реакций RiЕ внешних связей изображают на рисунке, иллюстрирующем результаты расчётов. Необходимо отметить, что сила Р лежит в соприкасающейся плоскости так же, как и ускорение a точки и имеет с ним одинаковое направление.
Дата добавления: 2015-05-30; просмотров: 1061;
