Точки в декартовой системе отсчёта. В первой задаче динамики известны уравнения движения точки: X = f1(t); Y = f2(t); Z = f3(t) и начальные условия этого движения
В первой задаче динамики известны уравнения движения точки: X = f1(t); Y = f2(t); Z = f3(t) и начальные условия этого движения. К начальным условиям движения точки отнесены: положение точки, характеризуемое координатами X0, Y0, Z0 в момент времени t0 = 0; проекции 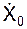 ,
, 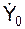 ,
, 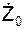 начальной скорости V0 при t0 = 0.
начальной скорости V0 при t0 = 0.
Алгоритм решения первых задач динамики предписывает чётко определённую последовательность действий исполнителя, которая приведена ниже.
1. Выбирают инерциальную систему отсчёта ОXYZ.
2. В системе отсчёта ОXYZ точку изображают в произвольный момент времени. При этом точка должна иметь координаты, значения которых больше нуля. Предполагают также, что точка движется в сторону возрастания координат ускоренно.
3. По исходным данным задачи определяют и изображают на рисунке начальные условия движения (X0, Y0, Z0, 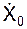 ,
, 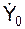 ,
, 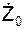 ).
).
4. К точке прикладывают активные силы FiE и реакции RiE внешних связей.
5. Записывают соответствующие выбранной системе отсчёта ОXYZ дифференциальные уравнения движения:
m· 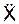 = Σ
= Σ 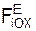 + Σ
+ Σ 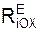 ;
;
m· 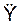 = Σ
= Σ 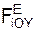 + Σ
+ Σ 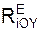 ;
;
m· 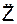 = Σ
= Σ 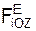 + Σ
+ Σ 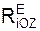 ,
,
где 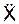 ,
, 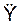 ,
, 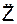 – проекции ускорения a на координатные оси; Σ
– проекции ускорения a на координатные оси; Σ 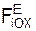 , Σ
, Σ 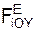 , Σ
, Σ 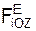 – суммы проекций активных сил FiE на соответствующие координатные оси ИСО; Σ
– суммы проекций активных сил FiE на соответствующие координатные оси ИСО; Σ 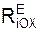 , Σ
, Σ 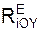 , Σ
, Σ 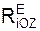 – суммы проекций реакций RiE внешних связей на оси ИСО.
– суммы проекций реакций RiE внешних связей на оси ИСО.
6. По заданным уравнениям движения X = f1(t); Y = f2(t); Z = f3(t) определяют проекции 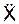 ,
, 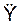 ,
, 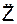 ускорения a точки на координатные оси.
ускорения a точки на координатные оси.
7. Найденные проекции 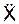 ,
, 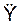 ,
, 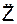 ускорения подставляют в дифференциальные уравнения движения точки.
ускорения подставляют в дифференциальные уравнения движения точки.
8. Определяют проекции POX, POY, POZ равнодействующей активных сил FiE и реакций RiE внешних связей на координатные оси:
POX = m· 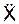 = Σ
= Σ 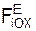 + Σ
+ Σ 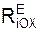 ;
;
POY = m· 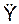 = Σ
= Σ 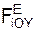 + Σ
+ Σ 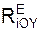 ;
;
POZ = m· 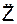 = Σ
= Σ 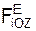 + Σ
+ Σ 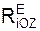 .
.
9. Определяют модуль Р равнодействующей активных сил FiE и реакций RiE внешних связей, действующих на точку:
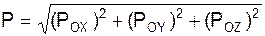 .
.
10. Для ориентации вектора Р равнодействующей активных сил и реакций внешних связей в пространстве определяют направляющие косинусы:
cos(P, i) = POX/P; cos(P, j) = POY/P; cos(P, k) = POZ/P.
11. По величине значений направляющих косинусов находят величины углов, составленных направлениями координатных осей системы отсчёта и направлением силы Р.
12. Равнодействующую Р активных сил FiЕ и реакций RiЕ внешних связей, действующих на точку, изображают на чертеже. Необходимо еще раз отметить, что ускорение a точки направлено так же, как и сила Р.
Дата добавления: 2015-05-30; просмотров: 1357;
