В декартовой системе отсчёта
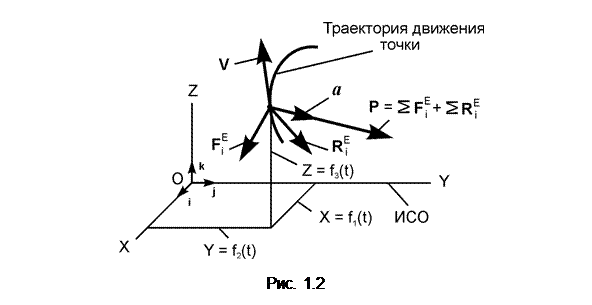 |
Рассмотрим движение несвободной материальной точки под действием активных сил FiЕ и реакций RiЕ внешних связей в инерциальной системе отсчёта OXYZ (рис. 1.2).
Для обозначения инерциальной системы отсчёта использована аббревиатура ИСО.
Три уравнения: X = f1(t); Y = f2(t); Z = f3(t) являются уравнениями движения точкив ИСО. Для рассматриваемой точки основное уравнение динамики имеет вид
m·a = P = ΣFiE + ΣRiE.
Спроецируем обе части последнего векторного равенства на координатные оси ИСО:
m· 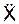 = Σ
= Σ  + Σ
+ Σ 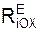 ;
;
m· 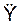 = Σ
= Σ  + Σ
+ Σ 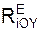 ;
;
m· 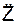 = Σ
= Σ  + Σ
+ Σ  ,
,
где 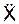 ,
, 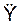 ,
, 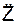 – проекции ускорения a на координатные оси; Σ
– проекции ускорения a на координатные оси; Σ  , Σ
, Σ  , Σ
, Σ  – суммы проекций активных сил FiE на соответствующие координатные оси ИСО; Σ
– суммы проекций активных сил FiE на соответствующие координатные оси ИСО; Σ 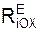 , Σ
, Σ 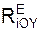 , Σ
, Σ  – суммы проекций реакций RiE внешних связей на оси ИСО.
– суммы проекций реакций RiE внешних связей на оси ИСО.
Произведение массы m точки и проекции её ускорения a на координатную ось инерциальной системы отсчёта OXYZ равно сумме проекций активных сил FiЕ и реакций RiЕ внешних связей на ту же ось.
Последние уравнения называют дифференциальными уравнениями движения несвободной материальной точки в декартовой инерциальной системе отсчёта.
Дата добавления: 2015-05-30; просмотров: 2015;
