В естественных координатных осях
Естественные координатные оси – прямоугольная система осей с началом в движущейся точке, направленных соответственно по касательной, главной нормали и бинормали к траектории этой точки.
Из известного студентам курса кинематики уравнение движения точки в естественных координатных осях имеет вид S = f(t), где S – дуговая координата.
Рассмотрим движение несвободной материальной точки под действием активных сил FiE и реакций RiE внешних связей в естественных координатных осях (касательная, главная нормаль, бинормаль). Для понимания излагаемого материала напомним некоторые положения, относящиеся к этому движению.
Как это отмечалось ранее, естественными координатными осями называют три взаимно-перпендикулярные оси: касательная (единичный вектор τ всегда направлен в сторону возрастания дуговой координаты S); главная нормаль (единичный вектор n направлен к центру кривизны траектории движения); бинормаль (единичный вектор b перпендикулярен векторам τи n и направлен так же, как и вектор k по отношению к векторам i, j в правой декартовой системе отсчёта OXYZ) (рис. 1.3).
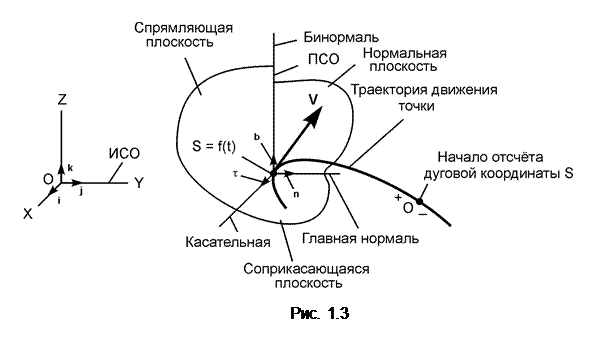
Начало естественных координатных осей всегда располагается на траектории в месте положения точки и, следовательно, перемещается вместе с точкой.
Таким образом, естественные координатные оси образуют подвижную систему отсчёта (ПСО).
Итак, рассматривается движение точки массой m в ПСО под действием активных сил и реакций внешних связей (рис. 1.4). Уравнение движения точки S = f(t) задано.
Из курса кинематики известно векторное выражение
a = aoτ + aon ,
где a – вектор ускорения точки; aoτ – вектор касательного ускорения; aon – вектор нормального ускорения.
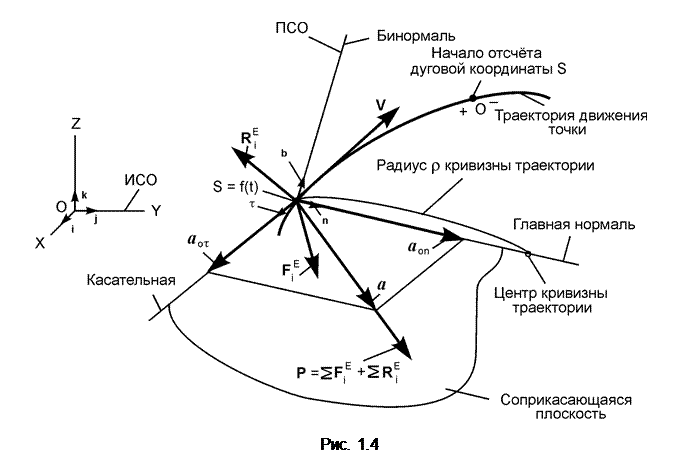
Спроецируем основное уравнение динамики m·a = ΣFiE + ΣRiE на координатные оси подвижной системы отсчёта:
m·aoτ = Σ 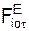 + Σ
+ Σ 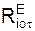 ;
;
m·aon = Σ 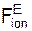 + Σ
+ Σ 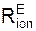 ;
;
m·aob = Σ 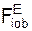 + Σ
+ Σ 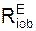 ,
,
где aoτ, aon, aob – проекции ускорения a соответственно на касательную, главную нормаль и бинормаль; Σ 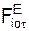 , Σ
, Σ 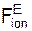 , Σ
, Σ 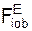 – суммы проекций активных сил на оси ПСО; Σ
– суммы проекций активных сил на оси ПСО; Σ 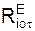 , Σ
, Σ 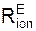 , Σ
, Σ 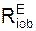 – суммы проекций реакций внешних связей на оси ПСО.
– суммы проекций реакций внешних связей на оси ПСО.
Известно также, что aoτ = 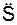 ; aon =
; aon = 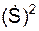 /ρ, где ρ – радиус кривизны траектории точки. При этом aob = 0, так как вектор ускорения aлежит в соприкасающейся плоскости и на бинормаль не проецируется. С учетом изложенного выше последние математические выражения приобретают вид:
/ρ, где ρ – радиус кривизны траектории точки. При этом aob = 0, так как вектор ускорения aлежит в соприкасающейся плоскости и на бинормаль не проецируется. С учетом изложенного выше последние математические выражения приобретают вид:
m· 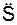 = Σ
= Σ 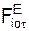 + Σ
+ Σ 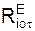 ;
;
m· 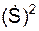 /ρ = Σ
/ρ = Σ 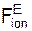 + Σ
+ Σ 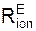 ;
;
Σ 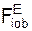 + Σ
+ Σ 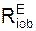 = 0.
= 0.
Произведения массы m точки и проекций её ускорения a на координатные оси ПСО равны сумме проекций активных сил FiЕ и реакций RiЕ внешних связей на те же оси ПСО.
Последние математические выражения называют дифференциальными уравнениями движения несвободной материальной точки в естественных координатных осях.
ПРИМЕЧАНИЕ. Дифференциальными уравнениями движения в естественных координатных осях удобно пользоваться тогда, когда точно известен вид траектории движения. В этом случае решение задачи существенно упрощается.
Дата добавления: 2015-05-30; просмотров: 1694;
